14. Prisma und Pyramide

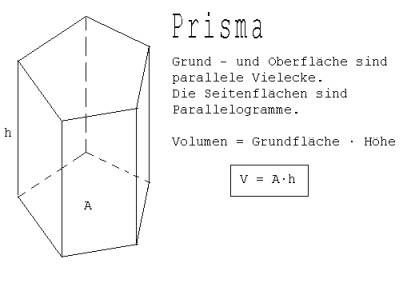
1. Prisma

 Abb. 1

2. Pyramide

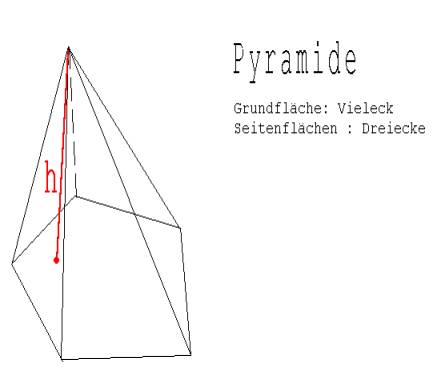
Abb. 2 

Nach dem Prinzip des Cavalieri ist   das Volumen   der   Pyramide  durch die Größe der Grundfläche und durch die Höhe bestimmt.

Prinzip des Cavalieri:

Zwei Körper haben gleiche Volumina, wenn sie in gleicher Höhe inhaltsgleiche Querschnittsflächen haben.

Nach Anklicken dieser Zeile wird dieses Prinzip veranschaulicht.

Es werden zwei Körper A und B verglichen. A ist ein Zylinder mit trichterförmiger Öffnung, B ist eine Halbkugel. 

Zwei Pyramiden mit gleicher Höhe und  inhaltsgleichen Grundflächen  haben  in  jeder  Höhe  inhaltsgleiche Querschnittsflächen und haben deshalb nach Cavalieri gleiche Volumina (siehe Abb . 3).

A₁= A₂

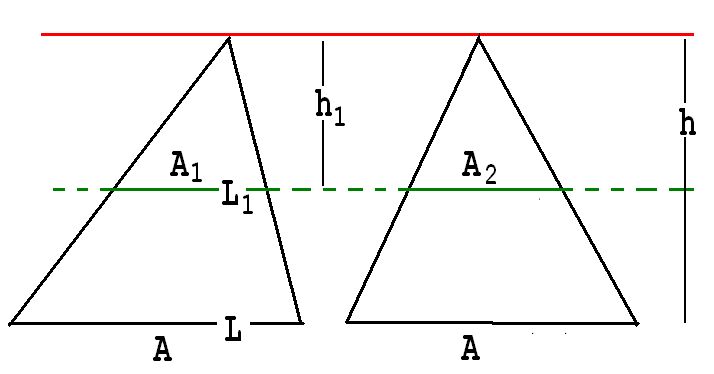
Abb. 3

Dies ist leicht einzusehen, denn eine Länge L₁ des Querschnitts verhält sich nach dem Strahlensatz zur entsprechenden Länge L der Grundfläche so wie h₁ zu h.

L₁ / L = h₁/h.

Ist die Grundfläche der Pyramide ein Dreieck, dann ist ihr Flächeninhalt A = ½∙a∙b ( a: Höhe, b: Länge der Grundseite). Für den der Grundfläche ähnlichen Querschnitt im Abstand h₁ von der Spitze gilt:

A₁= ½∙ a∙ (h₁/h)∙b∙( h₁/h) = ½∙a∙b ∙ ( h₁/h)² = A ∙ ( h₁/h)²

Dies bedeutet, dass der Flächeninhalt des Querschnitts nur von seiner Höhe und dem Inhalt der Grundfläche abhängig ist. Da eine Pyramide mit vieleckiger Grundfläche in Pyramiden mit dreieckigen Grundflächen aufgeteilt werden kann, gilt diese Aussage für jede Pyramide.

Nach einem Klick auf dieser Zeile wird gezeigt, dass ein Prisma in 3 Pyramiden mit gleichem Volumen aufgeteilt werden kann.

V(Pyramide) = 1/3·Grundfläche · Höhe

Das Volumen  einer Pyramide soll nun noch auf  eine Art bestimmt werden, wie sie in Abb. 4 angedeutet ist.

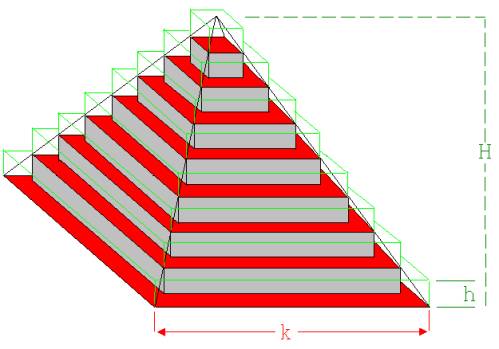
 Abb. 4

Es wird das Gesamtvolumen V₁ von n (n =1000) umbeschriebenen (grüne Ränder) und das Gesamtvolumen V₂ von (n-1) einbeschriebenen Quadern ( schwarze Ränder) berechnet. V₁ ist kleiner und V₂ ist größer als das Volumen der Pyramide. Wie an der Abbildung erkennbar ist, unterscheiden sich die beiden Volumina V₂ und V₁ durch das Volumen k² ∙ h/1000, dem Volumen des Quaders von V₁ mit der Nummer 1000. Da sich dieser Unterschied mit größer werdender Aufteilung von h dem Wert 0 annähert, streben V₂ und V₁ gegen einen gemeinsamen, das Volumen der Pyramide beschreibenden Grenzwert. Noch besser ist der Mittelwert V = (V₂ + V₁ ) /2 dem Volumen der Pyramide angepasst.

Das Volumen des kleinsten Quaders ist (k/1000)² ∙ h/1000 , das des darauffolgenden Quaders ist (2∙ k/1000)² ∙ h/1000. Für das Volumen V_Q des Quaders mit der Nummer l gilt: V_Q = (l∙ k/1000)² ∙ h/1000.

Zur Berechnung der Volumina wird n=999; l=l+1;a=a+(l*k/1000)^2 *h/1000;b=b+((l-1)*k/1000)^2 *h/1000; V=(b+a)/2 in das Fenster der von Rechner.php geschrieben. Sind im Variablenfeld dieser App. Werte für k und h eingetragen, dann wird zunächst „ mit Wiederholung“ und dann „Start“ angeklickt. Daraufhin wird a =V₁ , b = V₂ und V berechnet. Mit n=999 wird festgelegt, dass die Berechnung dann endet, wenn l den Wert 1000 erreicht.

Ergebnis der Rechnung: für h= 6 und k = 8: V= 128,0000 = h*k² / 3