4.5 Wahrscheinlichkeitsdichte und Fehlerverteilungsfunktion

4.5.1 Die Wahrscheinlichkeitsdichte

Die zufälligen Fehler f vieler gleichartiger Messungen sind nach einer Exponentialfunktion verteilt. Werden die Fehler in kleine, gleich große Intervalle um den wahren Wert W einsortiert, dann gilt für ihre Zahl n in einem Intervall mit der Intervallmitte f : n = A·e-(1/2)·(f/σ)^2 . Hierbei wird eine sehr große Zahl von Messwerten und sehr kleine Intervalle vorausgesetzt.

Nach Einführung des standardisierten Fehlers fs = f/ σ können wir stattdessen schreiben: n = A· e-(1/2)·fs^2.

Wie groß ist der Faktor A ?

A ist der Zahl N aller Messwerte und der Breite Δfs der Intervalls (bei kleinen Intervallen) proportional.

A/(N· Δfs ) = Konstante K   →    A = K·N· Δfs

n = K·N· Δfs· e-(1/2)·fs^2   →    n/ N = p = K·Δfs · e-(1/2)·fs^2    →    p/ Δfs = PD = K · e-(1/2)·fs^2

n/N ist die relative Häufigkeit für das Auftreten eines Fehlers fs im Intervall der Breite Δfs. Bei sehr großem N steht n/N für die Wahrscheinlichkeit p, mit der ein Messfehler fs im Intervall der Breite Δfs gefunden wird. p/Δfs wird als Wahscheinlichkeitsdichte PD des Fehlers fs bezeichnet.

K ist durch die Bedingung   K·-∞∫+∞ e-(1/2)·fs^2 dfs   =   2·K·o∫+∞ e-(1/2)·fs^2 dfs   = 1 festgelegt.

↓

2·K = 1/ o∫+∞ e-(1/2)·fs^2 dfs

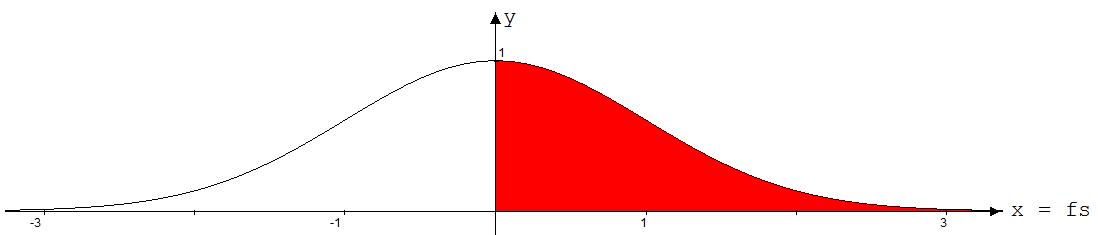
Zur Bestimmung von o∫+∞ e-(1/2)·fs^2 dfs wird der Graf von y = e-(1/2)·fs^2 mit „Mathe.-Physik“ - Rechenfenster ! - dargestellt, wobei fs mit x benannt wird (siehe Abb. 1).

Abb. 1

o∫+∞ e-(1/2)·fs^2 dfs gleicht dem Flächeninhalt der roten Fläche, für dessen Inhalt mit „Mathe_Flächeninhalt“ der Wert 1,254

ermittelt wurde.

↓

PD = 0,397· e-(1/2)·fs^2

Eine genauere Untersuchung zeigt: K= 1/√(2·π)

Der Graf zur Wahrscheinlichkeitsdichte PD = [1/√(2·π) ] · e-(1/2)·fs^2 ist in Abb.2 zu sehen.

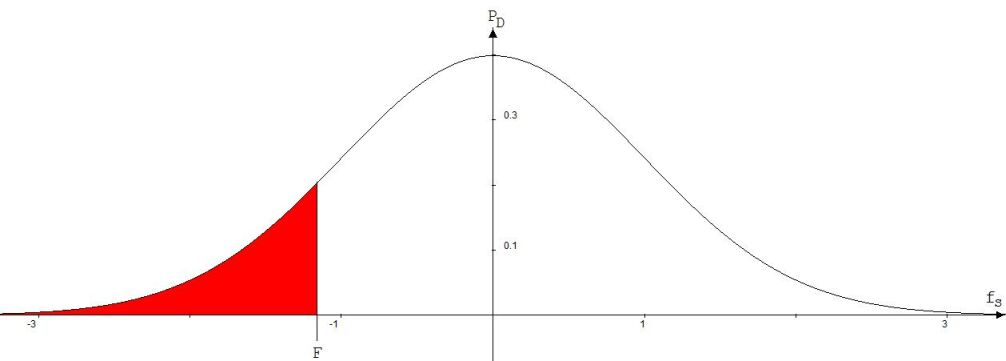
Abb. 2



4.5.2 Die Fehlerverteilungsfunktion

Der Flächeninhalt der in Abb. 2 sichtbaren roten Fläche steht für die Wahrscheinlichkeit P (fs≤F ) eines Fehlers fs≤F. Mit P (fs≤F ) hat man eine von F abhängige Funktion, die sogenannte Fehlerverteilungsfunktion. Die rote Kurve in der Abb.3 beschreibt diese Verteilungsfunktion in Abhängigkeit von F.

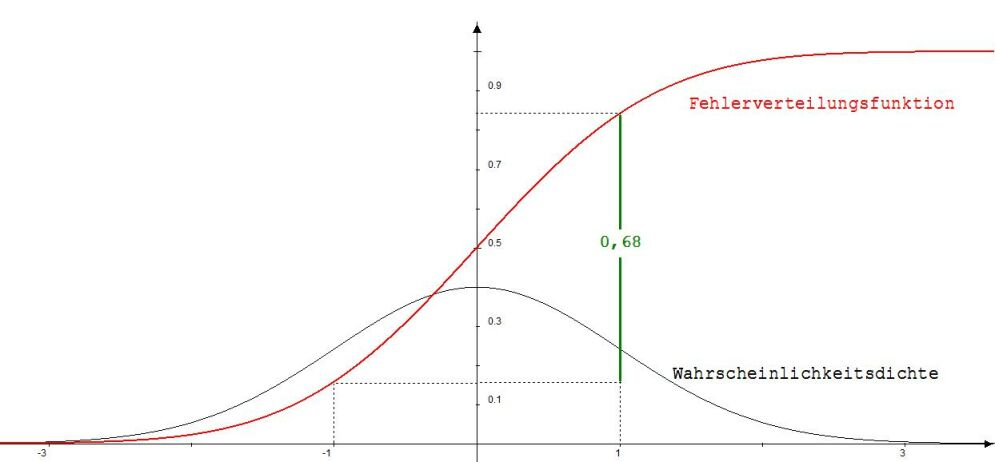
Abb. 3

Für P (fs≤0 ) kann der Wert 0,5 abgelesen werden. Die Wahrscheinlichkeit für einen Fehler < 0 ist demnach genauso groß wie die Wahrscheinlichkeit für einen Fehler > 0. Fast alle standardisierten Fehler liegen zwischen – 3 und + 3.  Demnach liegen   fast alle nicht standardisierten Fehler zwischen – 3σ und + 3σ. Wenn F von -1 auf +1 anwächst, dann nimmt die Wahrscheinlichkeit P (fs≤F ) um 0,68 zu. 0,68 ist demnach die Wahrscheinlichkeit dafür, dass |fs| ≤1 ist.

Die Darstellung der Verteilungsfunktion mit „Mathe.-Physik“ geschieht wie folgt:

Nach Wahl von „Tabelle bearbeiten_Anlegen einer Tabelle_Von der Einfügemarke an wird eine Spalte mit den Zahlen 1,2,3...angelegt“ wird eine Spalte mit den Zahlen 1,2,3....1000 geschriebent. Es sind die Nummern von 6000 Intervallen der Breite 6/1000 zwischen -3 und +3. Mit a*6/1000-3-3/1000 werden die x-Werte der Intervallmitten in eine zweite Spalte geschrieben (b-Werte). Die Wahrscheinlichkeiten 1/wrz(2*pi)*exp(-0.5*b^2) *6/1000 zu den Intervallen werden dann mit S+ 1/wrz(2*pi)*exp(-0.5*b^2) *6/1000 aufsummiert. S muss zuvor im Variablenfeld auf 0 gesetzt werden. Es entsteht eine Spalte mit den c-Werten P(fs≤b) . b steht in diesem Fall für F. Nach der Anweisung _b;c entsteht der Graf zur Verteilungsfunktion.

Es wird davon ausgegangen, dass Messfehler bei jeder Art Messung nach einer Exponentialfunktion verteilt sind. Damit diese Voraussetzung nicht ganz unbegründet bleibt, werden zwei weitere Beispiele zu ihrer Bestätigung behandelt.

Beispiel 2:

Mit Mathe.-Physik wird 15000 mal die relative Häufigkeit h1000  einer „6“ bei jeweils n = 1000 Würfen bestimmt. Die Differenzen h1000 - 1/6 sind als Messfehler f zu sehen.

Die standardisierten Fehler fs = f/σ werden, wie unten angegeben, ermittelt und nach ihrer Größe geordnet. Hiernach wird die zugehörende Funktion P(fs≤F ) bestimmt und deren Graf (siehe Abb.4) auf Übereinstimmung mit der in der Abb. 3 sichtbaren roten Kurve geprüft.

Die treppenförmig verlaufende Kurve in der Abb. 4 zeigt die Fehlerverteilung der zu den h1000 gehörenden Fehlern. Sie passt gut auf den roten Grafen.

Die senkrechten Strecken der zackigen Kurve weisen darauf hin, dass in der Fehlertabelle immer wieder mehrere gleiche Fehler aufeinander folgen. An der Längen dieser senkrechten Strecken erkennt man die relative Häufigkeit der Fehler gleicher Größe.

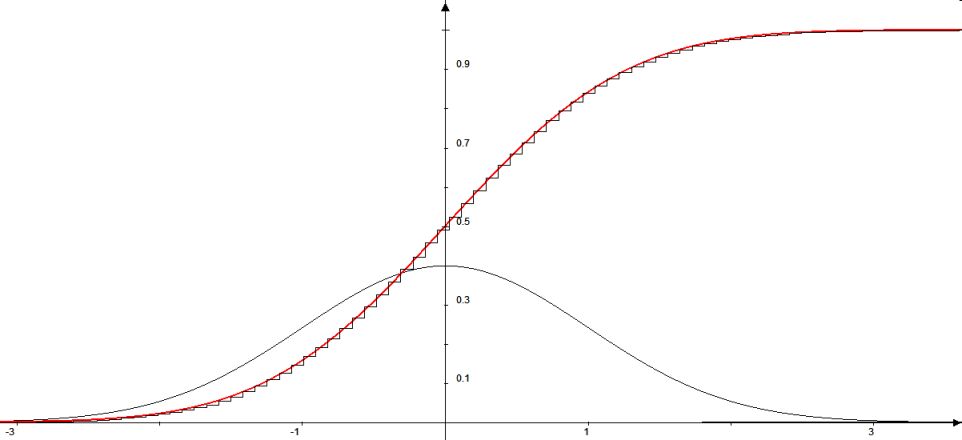
Abb. 4



Die einzelnen Schritte, die zu der zackigen Kurve führen, werden im Folgenden beschrieben.

 

1. Im Tabellenfenster wird mit „Tabelle bearbeiten_Anlegen einer Tabelle_ Es wird eine Spalte mit relativen Häufigkeiten des Ereignisses 6 angelegt“ eine Tabelle mit 15000 Werten h1000 angelegt.



 

Abb. 1

2. Mit dem Befehl   „a-1/6“  entsteht eine 2. Tabellenspalte mit Fehlern

Abb. 2

 

3. Die erste Spalte wird gelöscht mit „Tabelle bearbeiten_ Versetzen, Löschen, Anfügen_ Spalte wird von der Einfügemarke an gelöscht“ .

Übrig bleibt eine Spalte mit den Fehlern !

Anschließend werden mit „Tabelle bearbeiten_ Zeilen ordnen “ die Fehler nach ihrer Größe geordnet.



 

Abb. 3

4. Mit dem Befehl   „S+a^2“  wird die Summe der quadratischen Abweichungen ermittelt. S muss zuvor auf 0 gesetzt werden. Die Summe S aller a2  findet man in der 2. Spalte der letzten Zeile. Zur Berechnung der Standardabweichung wird unter die Tabelle k=wrz(S/15000) geschrieben. Bei einem Doppelklick auf diesem Term nimmt k  den Wert der Standardabweichung wrz(S/15000) an.

Abb. 4

 

5. Nach Löschen der zur Bestimmung von k erzeugten zweiten Spalte mit „Tabelle bearbeiten_ Versetzen, Löschen, Anfügen_ Spalte wird von der Einfügemarke an gelöscht“ wird mit dem Befehl  „a/k“  eine neue 2. Spalte mit  standardisierten Fehlern f/σ = fs angelegt.

Abb. 5

 

6. Nach dem Befehl „S +1/15000“ werden in die Zeilen relative Häufigkeiten für die Gesamtheit der Fehler geschrieben, die bis zu dieser Zeile berücksichtigt wurden.

Abb. 7

 

7. Nach passender Kalibrierung des Bildfeldes mit „Maße des Bildfeldes festlegen“  (siehe unterer Rand des Tabellenfensters !) wird mit dem  Befehl „_b;c“ die Zeichnung eines Verteilungsdiagramms ( siehe Abb.4) veranlasst.




Die zu den h1000 gehörende Varianz kann auch ohne Kenntnis von Werten h1000 ermittelt werden.
Für ein  h1000 kann geschrieben werden:  h1000 = (1 + 0 + 1 + 0 + 0 + 0 + 0 .......)/1000.  Die i. Zahl (1 oder 0) aus 1000 Zahlen zeigt an, ob der i. Wurf mit „6“ oder  mit „≠ 6“ endete. Für die verschiedenen h1000 schreiben wir:
h1000 = (x1 + x2 + x3 + x4 ....... + x1000) /1000
De Zufallsvariable x1 steht für das Ergebnis des ersten Wurfs ( 1 oder 0), x2 für das des zweiten Wufs usw..

σx2 ist die Varianz dieser Zufallsvariablen.

h1000 = (x1 + x2 + x3 + x4 ....... + x1000) /1000 = x1/1000  + x2/1000  + x3/1000  + x4/1000  ....... + x1000/1000

Die Varianz von xi/1000 ist σx2 /10002 .    σ2 , die Varianz von h1000 , erhält man durch Addition der zu xi/1000 gehörenden Varianzen.

σ2 = 1000 · ( σ x / 1000 )2 = σ x2 /1000

 Die Varianz σx2 von xi (x1 oder x2 ...) ist die mittlere quadratische Abweichung der Variablen xi von p = 1/6 (Mittelwert von xi). Diese Varianz ist leicht berechenbar. Bei  5/6  einer sehr großen Zahl n von Würfen hat xi  den Wert  0, somit ist seine quadratische Abweichung von p = 1/6 gleich (0- 1/6)2  = (1/6)2. Bei 1/6  der n Würfe ist  xi gleich 1 und die quadratische Abweichung (1- 1/6)2 = (5/6)2 .

→ σx2 = [5/6 · n · (1/6)2 + 1/6 ·n ·(5/6)2 ] / n

→  σx2   =   5/6 · (1/6)2 + 1/6 ·(5/6)2   =   (1/6) · (5/6) · (1/6 + 5/6)

→  σx2   =   (1/6) · (5/6)   =  (1/6) ·(1 – 1/6) = p · (1- p) = 0,1388

→  σ2 = p · (1- p) /1000 = 0,0001388

Für die Varianz von hn ( relative Häufigkeit bei n Würfen) gilt: σ2 = p · (1 – p )/n 


Beispiel 3:

Klickt   man   im Programm   „Mathe.-Physik“   unter „Simulation“ den Menüpunkt  „Rotierender Zeiger zur Untersuchung einer Schwingung_senkrechte Schwingung“    an, dann erscheint ein  rotierender Zeiger, der an seinem Ende eine waagrechte Strecke mit einer zuvor festgelegten Umlaufzeit z.B. 2 s auf und ab führt. Bei   einem Mausklick (Linksklick) während der Rotation wird der Zeitunterschied zum letzten Mausklick in das Tabellenfenster II eingetragen. Der Eintrag beginnt mit dem 2. Mausklick. Drückt man immer dann auf die linke Maustaste, wenn die waagrechte Strecke ihre höchste Lage erreicht, dann erscheint im Tabellenfenster II eine Tabellenspalte mit Umlaufzeiten. Der Fehler einer solchen Zeitmesswerts ist dessen Abweichung von 2s. 1000 Messwerte wurden aufgenommen und zu dessen Fehlern die Häufigkeitsverteilung bestimmt. Der ihr zugeordnete Graf ist in der Abb.8 neben der roten Kurve zu sehen, von der er nur durch kleine Unregelmäßigkeiten abweicht.

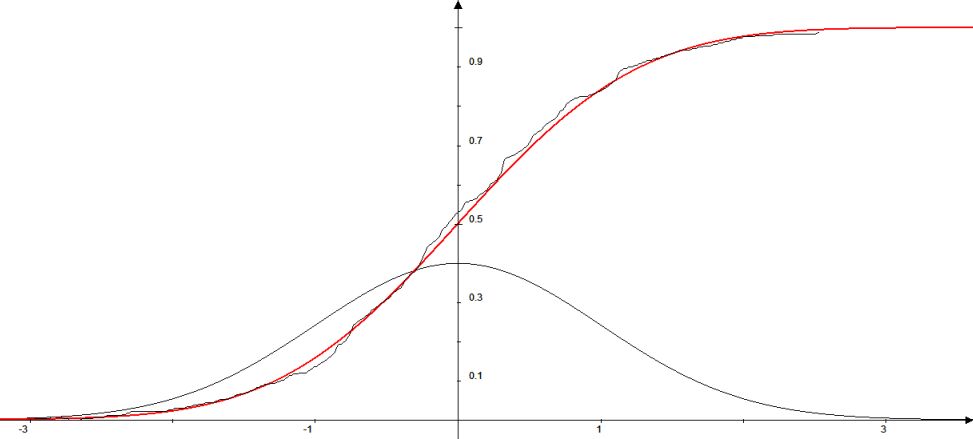
Abb. 8