Fehler von Summen, Differenzen, Produkten und Quotienten

4.3 Fehler von Summen, Differenzen, Produkten und Quotienten

4.3.1 Die Varianz einer Summe und einer Differenz

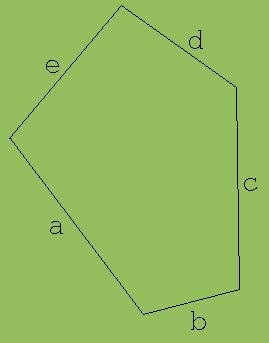
Abb. 1

Wir nehmen an, dass die Varianz einer Summe gleich der Summe aus den Varianzen der Summanden ist und schreiben demgemäß:

σ_U’² = 5 · σ_a²

Hier wird vorausgesetzt, dass die Varianz einer Summe gleich der Summe aus den Varianzen der Summanden ist (die Summanden können auch negativ sein !).

σ_a’±b’² = σ_a’² + σ_b’²

Zur Bestimmung des Umfangs U eines Fünfecks (siehe Abb. 1) werden die Seiten a, b, c, d und e gemessen und anschließend die Summe U’ aus diesen Messwerten a’, b’, c’, d’, e’ zu den Seiten a, b, c, d, und e gebildet. Wenn alle 5 Seiten mit der gleichen Genauigkeit gemessen werden, dann ist

σ_a’² = σ_b’² = σ_c’² = σ_d’² = σ_e’²

Wir nehmen an, dass die Varianz einer Summe gleich der Summe aus den Varianzen der Summanden ist und schreiben demgemäß:

σ_U’² = 5 · σ_a²

Hier wird vorausgesetzt, dass die Varianz einer Summe gleich der Summe aus den Varianzen der Summanden ist (die Summanden können auch negativ sein !).

σ_a’±b’² = σ_a’² + σ_b’²

Beweis:

a’ und b’ sind Messwerte von a und b mit den Fehlern f_a’ und f_b’.

(f_a’ ± f_b’)² = f_a’² + f_b’² ± 2 · f_a’· f_b’

Die Summe aller Produkte 2 · f_a’· f_b’ ist 0, denn ein bestimmter Fehler f_a’ trifft in einem Produkt mit einem bestimmten Fehler f_b’ genauso häufig zusammen wie mit dem Fehler – f_b’.

Somit kann geschrieben werden: Σ(f_a’ ± f_b’)²= Σ f_a’² + Σ f_b’².

Der Mittelwert von (f_a’ ± f_b’)² gleicht der Summe aus den Mittelwerten von f_a’² und f_b’².

→ σ_a’±b’² = σ_a’² + σ_b’²

4.3.2 Die Varianz eines Produktes und eines Quotienten

^{Bei
Produkten a’· b’ und Quotienten a’/b’
ist die Berechnung der zugehörigen Varianzen σ}_a’·b’^{2
und σ}_a’/b’^{2
aus σ}_a’^{2
und σ}_b’^{2
nicht so einfach, weil die Fehler dieser Terme nicht durch Addition
bzw. Subtraktion aus den Fehlern ihrer Glieder berechnet werden
können. Ein einfaches Additions– bzw.
Subtraktionsgesetz gilt jedoch für Fehler der
Verhältnisse a* = a’/a und b* = b’/b (a und b
sind die wahren Größenwerte).}

Beweis der Behauptung:

f_a*·b* = (1 + f_a*) · (1 + f_b* ) – 1 = f_a* + f_b* + f_a* · f_b*

Die Fehler sind Abweichungen von 1 !

f_a* · f_b* ist gegenüber f_a* + f_b* vernachlässigbar klein. → f_a*·b* ≈ f_a* + f_b*

f_a*/
b* = (1 + f_a*) / (1 + f_b* ) – 1 = ( f_a* - f_b* ) / (1 - f_b*)

f_b* ist gegenüber 1 vernachlässigbar. → f_a*/
b* ≈ f_a* - f_b*

→ σ_a*·b*² = σ_a*² + σ_b*² ; σ_a*/b*² = σ_a*² + σ_b*²

Wie soll nun σ_a’·b’² berechnet werden, wenn σ_a’²und σ_b’² bekannt sind ?

σ_a*² = σ_a’²/ a² ; σ_b*² = σ_b’²/ b² , σ_a*·b*² = σ_a’·b’² / (a² · b²)

→ σ_a’·b’² /( a² · b²) = (σ_a’²/ a² + σ_b’²/ b²) → σ_a’·b’² = (σ_a’²/ a² + σ_b’²/ b²) · ( a² · b²)

Zur Berechnung von σ_a’·b’² werden für a und b die Mittelwerte von a’ und b’ eingesetzt.