4.2 Varianz und Standardabweichung

Es ist nun zu verstehen, dass ein einzelner Messwert nicht zur Beschreibung einer Größe (Länge, Kraft, Wahrscheinlichkeit ...) geeignet ist. Auch ein Mittelwert M vermittelt nur dann eine Vorstellung von einer Größe, wenn  neben ihm noch eine Angabe über den möglichen zufälligen Fehler gemacht wird.

Wie soll dies geschehen ?

Vielleicht kommen wir weiter, wenn wir uns an einem Messbeispiel ein Bild über die Häufigkeit bestimmter Fehler machen. Das folgende Experiment ist zu diesem Zweck empfehlenswert (siehe Abb. 1).

Abb. 1

Abb. 2

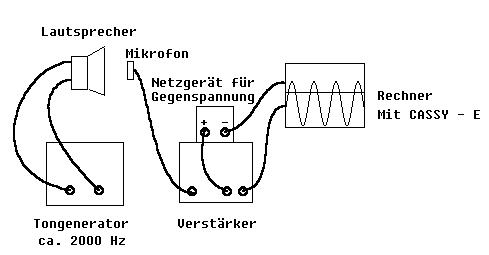
Ein 2000 Hz - Ton wird mit einem Mikrofon aufgenommen und nach Verstärkung des Signals auf ±1,5V mit Hilfe Rechners mit AD-Wandler (CASSY - E) registriert. Durch eine gegen das Messsignal wirkende konstante Gegenspannung erreicht man, dass die positiven Halbwellen nicht über 0,5 V hinausgehen (siehe Abb.2 ). So können die Höhen der Spannungsspitzen in den empfindlichen Messbereichen ±1V und ± 0,3 Volt gemessen werden, in denen die Schwankungen des Messsignals gut erkennbar sind. Je Sekunde werden 2000 Spannungsspitzen ausgemessen. Der Messbereich wird vom Rechner in 256 gleich große Intervalle aufgeteilt. Über jedem Intervall errichtet der Rechner auf seinem Bildschirm eine senkrechte Strecke, deren Länge proportional zur Zahl der Messwerte ist, die je Sekunde in dieses Intervall fallen (Zahl aller Messwerte im Intervall / Zeit der Messwertaufnahme).

In den Abb. 3 und 4 sind Ergebnisse dargestellt, die im Messbereich ±1V aufgenommen wurden. Deutlich ist zu sehen, wie die Diagramme mit zunehmender Anzahl von Messungen mehr und mehr eine Glockenform annehmen.

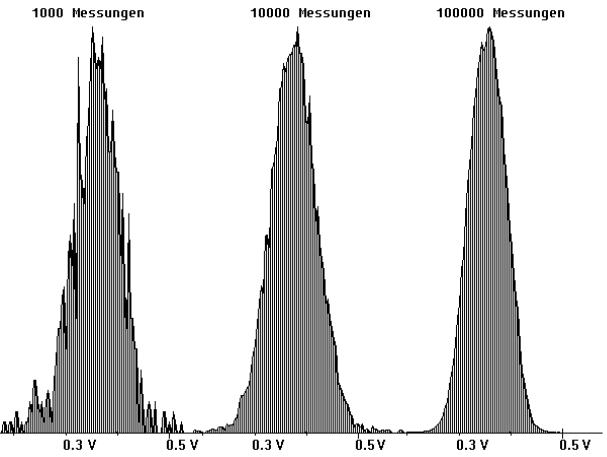
Abb. 3

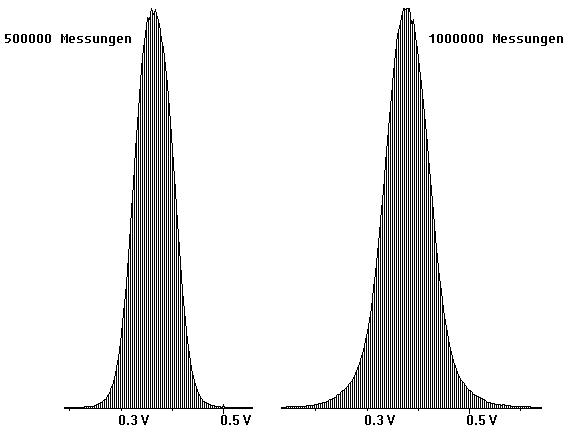
Abb. 4

Eine mathematische Untersuchung soll nun an dem Diagramm in Abb. 5 durchgeführt werden. Diese Verteilungskurve zu 1000000 Messungen, welche die Spitzen der erwähnten, nicht mehr dargestellten senkrechten Strecken verbindet, wurde mit der Gegenspannung -1,374V in dem Messbereich ±0,3V aufgenommen. Die Kurve sieht so aus, als ob die Zahl der Messwerte f(x) in einem Intervall um einen Messwert x mit einer Exponentialfunktion f(x) = A·e^{-b·(x-W)^2} beschrieben werden könne. (x-W)^2 steht für (x-W)². W ist der wahre Wert 0,126 V und (x-W) ist der Fehler f des Messwerts, seine Abweichung von W.

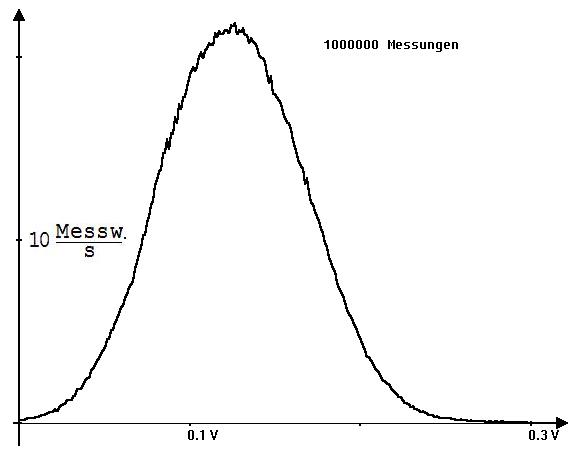
Abb. 5

Mit „Mathe.-Physik“ kann der Verteilungskurve ein Graf mit f(x) = 21,7 · e^{[-280·(x-0,126)^2]} angepasst werden (siehe Abb. 6). Ein Term der Form A·e^{-b·f^2} beschreibt demnach die Zahl der Messwerte in dem Intervall des Fehlers f.

Es wird davon ausgegangen, dass eine exponentiellen Fehlerverteilung nach A·e^{-b·f^2} für jede Art von Messung gilt, weshalb es sinnvoll erscheint, an ihr ein geeignetes Maß für deren Ungenauigkeit zu suchen.

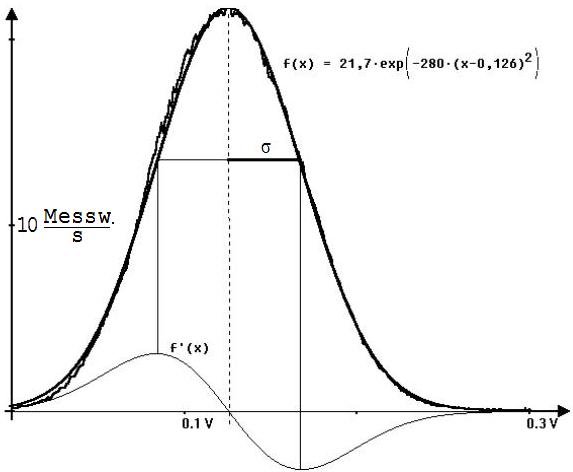
Abb. 6

Der neben dem quadratischen Term (x-0,126)² = f² stehende Faktor ist für die Breite der Glockenkurve maßgebend. Er ändert sich nicht, wenn der Messbereich feiner aufgeteilt wird, wenn z.B. statt 256 Intervallen 512 Intervalle gewählt werden, nur A würde in diesem Fall halbiert. Es liegt nahe, diesen Faktor als Maß für die Ungenauigkeit der Messwerte zu nehmen. Da diese Größe aber nicht veranschaulicht werden kann, sollte man einen anderen die Glockenkurve kennzeichnenden Wert suchen, welcher diesen Nachteil nicht hat. In Frage kommt der Abstand σ eines Wendepunkts vom wahren Wert W.

Wendepunkt: Übergang von einer Rechtskurve in eine Linkskurve bzw. einer Linkskurve in eine Rechtskurve. Die 1. Ableitung von f(x) hat an einem Wendepunkt ein Extremum.

Durch σ ist auch der Wert b genau bestimmt.

Es gilt: 1 = 2· b ·σ² → b = 1 / (σ² ·2)

↓

A·e^{-b·f^2} = A·e^{- 0,5 · f^2 /σ^2} = A·e^{- 0,5 · (f/ σ)^2}

f/σ heißt standardisierter Zufallsfehler fs.

A·e^{-b·f^2} = A·e^{- 0,5 · (f/ σ)^2} = A·e^{- 0,5 · fs^2}

σ kann nur dann als sinnvolles Maß für die Genauigkeit der Messwerte eingeführt werden, wenn mit einer zumutbaren Zahl von Messwerten ohne großen mathematischen Aufwand auf σ geschlossen werden kann. Dies ist möglich, denn es kann bewiesen werden, dass σ² gleich dem Mittelwert aus den Quadraten der Fehler f ist.

σ² = Mittelwert der f²

Bei den nachfolgenden Untersuchungen werden derart kleine Fehlerintervalle vorausgesetzt, dass die Differenzen zwischen den Fehlern eines Intervalls vernachlässigbar sind. Für die Summer S aller f² innerhalb eines Intervalls um f können wir deshalb schreiben: S = f²·A·e^{-b·f^2} . Zur Bestimmung des Mittelwerts von f² ist die Summe aller Produkte f²·A·e^{-b·f^2} durch die Zahl N aller Messwerte zu teilen. A·e^{-b·f^2} Messwerte gehören zu einem Intervall. N = ΣA·e^{-b·f^2} ist die Summe aller A·e^{-b·f^2} .

Mittelwert aus f² = Σf²·A·e^{-b·f^2} / ΣA·e^{-b·f^2} = Σf²·e^{-b·f^2} / Σe^{-b·f^2} = (1/b) ·Σb·f²·e^{-b·f^2} / Σe^{-b·f^2}

Zur Berechnung des Quotienten kann man sich wegen der Symmetrie der Glockenkurve auf die positiven Fehler beschränken. Für f·√(b) schreiben wir z.

Mittelwert aus f² = (1/b) · Σz²·e^{-z^2} / Σe^{-z^2}

Σz²·e^{-z^2} / Σe^{-z^2} ist bei sehr schmalen Intervallen unabhängig von der Breite der gewählten Intervalle gleich 1/2.

Somit gilt: Mittelwert aus f² = 1/(2·b) = σ²

Der Mittelwert von f² = σ² heißt Varianz und σ, die Wurzel aus diesem Mittelwert, trägt den Namen Standardabweichung.

Wie groß ist die Wahrscheinlichkeit P(|f| ≤ F) für einen Fehler f, dessen Betrag nicht größer ist als ein bestimmter Wert F z.B. F = σ ?

Die Wahrscheinlichkeit p, mit der ein Messwert mit einem Fehler f aus einem bestimmten Intervall behaftet ist, erhält man, indem man die Zahl der zu diesem Intervall gehörenden Messwerte durch die Zahl aller Messwerte teilt.

p = A · e^{-(1/2)· fs^2} / ΣA · e^{-(1/2)· fs^2} = e^{-(1/2)· fs^2} / Σe^{-(1/2)· (fs)^2}

p = e^{-(1/2)· fs^2} / Σe^{-(1/2)· fs^2}

Zur Berechnung von P(|f| ≤ F) = P(|fs| ≤ F/σ) muss die Summe der zu den Intervallen mit |fs| ≤ F/ σ gehörenden Werte e^{-(1/2)· fs^2} durch Σe^{-(1/2)· fs^2} geteilt werden. Hierbei kann man sich wieder auf die positiven fs beschränken.

Ergebnis:

Bei sehr vielen Messwerten fallen 68% der Werte in den Bereich W± σ. Das heißt ein Messwert M hat mit der Wahrscheinlichkeit 0,68 einen Fehler f mit einem Betrag ≤ σ. 95% aller Messwerte fallen in den Bereich W± 1,96· σ. Dies gilt allgemein bei einer Fehlerverteilung nach f(fs) = A · e^{-(1/2)· fs^2} .

Der mittlere Fehler des Mittelwerts

Eine Größe wird normalerweise mit einem Mittelwert aus mehreren Einzelwerten beschrieben. Da die Mittelwerte weniger schwanken als die Einzelwerte, ist die Standardabweichung σ_M der Mittelwerte das angemessene Fehlermaß.

Die Varianz σ_M² der Mittelwerte nimmt mit der Zahl n der Werte ab, die zur Bildung des Mittelwerts genommen werden.

Vermutung: σ_M² = σ²/n

n ist die Zahl der Messwerte, aus denen ein Mittelwert gebildet wird, σ² ist die Varianz der Einzelwerte

In der Regel ist der „wahre Wert“ nicht bekannt.  Wie soll  σ  in einem solchen Fall bestimmt werden ?

Der Mittelwert  aus vielen Messwerten wird statt des „wahren Wertes“ zur Berechnung der quadratischen Abweichungen genommen. Je mehr Einzelwerte verwertet werden, desto geringer ist der Unterschied zwischen den Abweichungen vom wahren Wert und den Abweichungen vom Mittelwert. Die Differenz zwischen der Varianz σ² in Bezug auf den wahren Wert und der Varianz σ'² in Bezug auf den Mittelwert nimmt mit steigender Varianz σ_M²  des Mittelwerts zu.

Vermutung: σ² - σ'² = σ_M² 

Aus dieser Vermutung, die noch zu beweisen ist, können wichtige Schlüsse gezogen werden:

σ² = σ'² + σ_M²  →    σ² = σ'² + σ² / n   →    σ² · (1 – 1/n) = σ'²   →    σ² = σ'² · [n / (n-1)]

σ'² = (f₁² + f₂² + f₃²...... + f_n² )/n

σ² = σ'² · [n / (n-1)] = (f₁² + f₂² + f₃²...... + f_n² )/(n-1)

Für die Varianz σ_M² des Mittelwerts von Messwerten gilt somit:

σ_M² = (f₁² + f₂² + f₃²...... + f_n² )/[(n-1) · n ]

σ_M = √{(f₁² + f₂² + f₃²...... + f_n² )/[(n-1) · n ]}

Ein Messergebnis wird in der Form „Mittelwert ± σ_M“ angegeben. σ_M heißt auch mittlerer Fehler des Mittelwerts