1.11.4 Berechnung der  Trägheitskräfte in einem rotierenden System mit Hilfe der Differentialrechnung

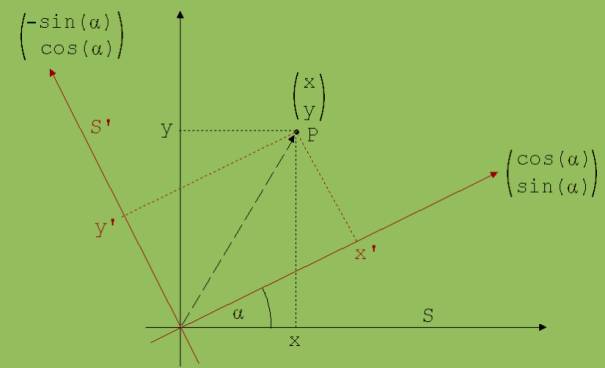
Wir stellen uns eine rotierende  Ebene mit einem auf ihr festgelegten x’, y’- Koordinatensystem vor. Der Drehpunkt sei der 0-Punkt des Koordinatensystems (siehe Abb. 1). Zum Zeitpunkt t = 0 stimme das mit der Winkelgeschwindigkeit ω rotierende x’, y’-System S’ mit einem ruhenden x, y – System S überein. Zu einem späteren Zeitpunkt bilde die x’ –Achse  mit der x-Achse  den Winkel α = ω·t.  Ein Massepunkt P mit der Masse m hat in S die Koordinaten x, y und in S’ die Koordinaten x’, y’ .

Abb. 1

Ortvektor {x;y} = r

Einheitsverktoren der x' - und y'-Achse: e_x = {cos(ω·t); sin(ω·t)} und e_y = {-sin(ω·t); cos(ω·t)}

Zur Bestimmung der Scheinkräfte in S' muss m·{ d²x’/dt², d²y’/dt²} bestimmt werden.

x' = x · cos(ω·t) + y · sin(ω·t) = e_x · r,     y' = -x · sin(ω·t) + y · cos(ω·t) = e_y · r

de_x /dt = ω·{-sin(ω·t); cos(ω·t)}= e_y · ω,       de_y /dt = - ω· {cos(ω·t); sin(ω·t)} = -e_x · ω

1.)

dx'/dt = de_x /dt· r + e_x · { dr/dt; dy'/dt } = e_y · ω· r + e_x · dr/dt

dy'/dt = de_y /dt· r + e_y · { dr/dt; dy'/dt } = -e_x · ω· r + e_y · dr/dt

d²x’/dt² = de_y /dt · ω · r + e_y · ω · dr/dt + de_x /dt · dr/dt + e_x · d²r/dt²

d²y’/dt² = -de_x /dt · ω · r + e_x · ω· dr/dt + de_y /dt · dr/dt + e_y · d²r/dt²

↓

2.)

d²x’/dt² = -e_x · ω· ω· r + 2·e_y · ω · dr/dt + e_x· d²r/dt²

d²y’/dt² = -e_y · ω· ω· r - 2·e_x · ω · dr/dt + e_y· d²r/dt²

Die Gleichungen 1 werden nach e_x · dr/dt und e_y · dr/dt aufgelöst und die für sie stehenden Terme

dx'/dt - e_y · ω· r , dy'/dt + e_x · ω· r in die Gleichungen 2 für e_x · dr/dt und e_y · dr/dt eingesetzt.

d²x’/dt² = e_x · ω²· r + 2·ω· dy'/dt + e_x · d²r/dt² = e_x · ω²· r + 2·ω· v'_y + e_x · d²r/dt²

d²y’/dt² = e_y · ω²· r - 2 · ω· dx'/dt + e_y · d²r/dt²= e_y · ω²· r - 2 · ω· v'_x + e_y · d²r/dt²

{ dx’/dt; dy’/dt } = {v'_x ; v'_y }

Der Beobachter in S' ordnet dem Körper mit der Beschleunigung { d²x’/dt² ; d²y’/dt² } und der Masse m die

Kraft F' = m·{ d²x’/dt², d²y’/dt² } zu.

F' = m · ω²· {x' ; y'} + 2· m ·ω· {v'_y ; -v'_x } + m ·{ e_x · d²r/dt²; e_x · d²r/dt²}

m ·{ e_x · d²r/dt², e_x · d²r/dt²} ist die in S' dargestellte wirkliche Kraft F.

F' = m · ω²· {x' ; y'} + 2· m ·ω· {v'_y ; -v'_x } + F

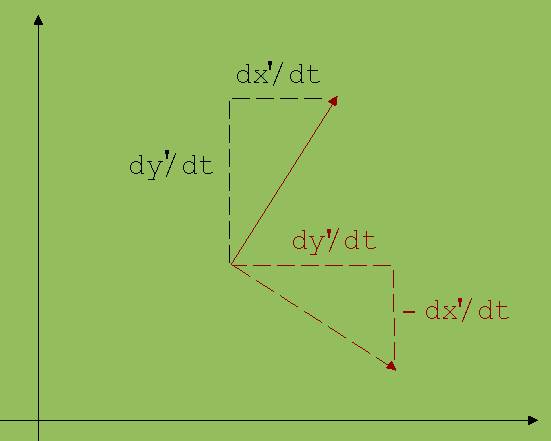
Abb. 2

2 · m · ω ·{ v’_y’ ; - v’_x’ }  beschreibt die Coroliskraft und  m · ω² · {x’; y’} die Zentrifugalkraft.

{dy’/dt ; - dx’/dt} = { v’_y’ ; - v’_x’}   ist ein Vektor, der durch eine Rechtsdrehung um 90° aus dem Geschwindigkeitsvektor { v’_x’ ; v’_y’ } entsteht. { v’_x’ ; v’_y’} steht für den Geschwindigkeitsvektor im System S’.   {x’; y’}  ist der Ortsvektor von P in S’  mit dem Betrag r. Als Beträge der beiden Trägheitskräfte (Scheinkräfte) erhalten wir: 2 · m · ω ·|v’| und m · ω² · r.