1.13.3 Die stehende Welle (Interferenz)

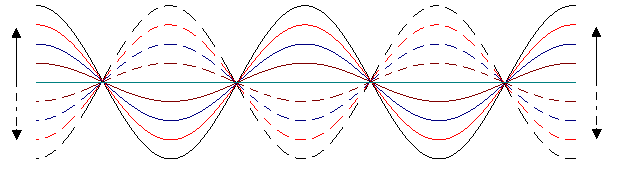
Wir stellen uns ein straff gespanntes Seil vor, dessen beide Enden periodisch mit gleicher Frequenz auf und ab bewegt werden. Es bildet sich hierbei eine als stehende Welle bekannte Schwingungsform aus, die durch Stellen der Ruhe ( Knoten ) und Stellen maximaler Bewegung (Bäuche ) ausgezeichnet ist ( siehe Abb.1 ).

Abb. 1

Eine Vorführung über die Bewegung zwischen zwei Knoten erfolgt nach „53“ und „START“

Die Änderung des Wellenträgers an einer bestimmten Stelle erhält man durch Addition der von den beiden Erregern ausgehenden Einzelwirkungen u₁ und u₂. Somit kann die von einer stehenden Welle verursachte Zustandsänderung als Summe u₁ + u₂ dargestellt werden. u₁ beschreibt eine vom linken Erreger und u₂ eine vom rechten Erreger ausgehende Welle.

Dieser als Interferenz (Überlagerung ) bekannte Sachverhalt wird durch Abb. 2 veranschaulicht. Die blauen und roten Sinuslinien beschreiben Einzelwirkungen u₁ und u₂ der nach rechts und links laufenden Wellen. Mit der schwarzen Sinuslinie ist u₁+ u₂ dargestellt. Deutlich sind die Stellen ( Knoten ) zu erkennen, an denen sich die Einzelwirkungen aufheben. Der Abstand zweier benachbarter Knoten beträgt eine halbe Wellenlänge λ /2

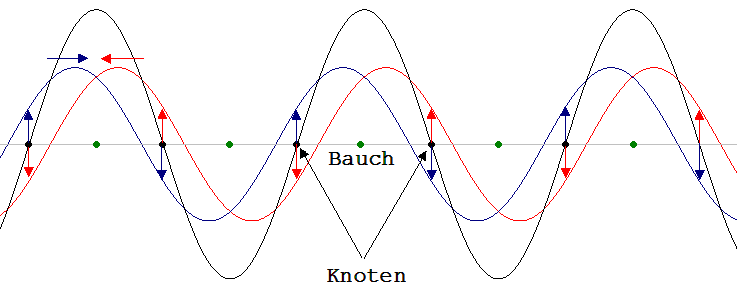
Abb. 2

Eine Vorführung dieser Überlagerung erfolgt mit „172“ und „START“

Die blaue Kurve beschreibt die stehende Welle !

Eigenschwingungen von Wellenträgern

Bewegt man ein Endstück A eines beidseitig eingespannten, straffen Seils periodisch nach oben und unten, dann wird man entdecken, dass sich bei bestimmten Frequenzen eine stehende Welle entwickelt, die auch dann noch erhalten bleibt, wenn man das Seil nicht mehr bewegt. Es handelt sich hierbei um eine Eigenschwingung. Ihre Bildung kann durch Interferenz zweier Wellen erklärt werden. Die eine Welle geht von A aus, die andere ist das Ergebnis einer Reflexion am anderen Ende B.

Bei einer Eigenschwingung muss die Welle nach zweimaliger Reflexion an A und B so beschaffen sein als ob sie von A ausginge. Die Knoten an den Enden des Seils zeigen an, dass die Einzelwirkung u einer Welle bei Reflexion am festen Seilende umgekehrt wird (Phasenumkehr). Aus u wird – u. Nach zweimaliger Reflexion wirkt sich diese Phasenumkehr nicht aus. Deshalb ist die Bedingung für eine Eigenschwingung erfüllt, wenn die Laufzeit t einer Welle für den Weg von einem Ende zum andern und wieder zurück (2 Reflexionen) ein Vielfaches der Schwingungszeit T ist.

t = n·T (n: natürliche Zahl )

t·v = 2·L ; L: Länge des Seils, v: Wellengeschwindigkeit

↓

n · T·v = 2·L → T = 2·L/(n·v) → f = n·v/(2·L)

Auf einem eingespannten Seil sind demnach mehrere Eigenschwingungen möglich. Die Schwingung mit n = 1 heißt Grundschwingung, die mit n = 2 erste Oberschwingung usw. .

Für die Wellenlängen λ der interferierenden Wellen gilt: v = λ · f → λ = v/f

↓

λ = v/f; f = n·v/(2·L)      →      λ = 2·L/n     →     L = n· λ /2

Bei der Grundschwingung ist die gesamte Seillänge gleich der halben Wellenlänge. Da zwei benachbarte Knoten eine halbe Wellenlänge voneinander entfernt sind, gibt es bei der Grundschwingung neben den Seilenden keine weiteren Knoten. Die erste Oberschwingung hat einen dritten Knoten in der Mitte.

Die hier beschriebene Phasenumkehr wird nach „190“ und „START“ dargestellt.

Eigenschwingungen in einer Wasserwanne

Erzeugt man eine Welle in einer mit Wasser gefüllten Wanne, dann bildet sich eine stehende Wasserwelle aus, deren Schwingungen mit Hilfe der Experimentierwippe registriert werden können.

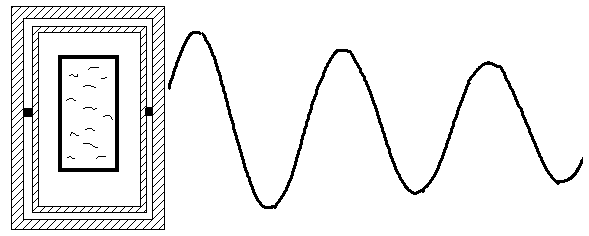
Abb. 3

Bei einer Grundschwingung ist die Länge L der Wanne gleich λ /2. Die Wellengeschwindigkeit v kann in diesem Fall nach v = λ ·f = 2·L·f berechnet werden

Eigenschwingungen einer Schraubenfeder

Die Länge L einer beidseitig eingespannten, schwingenden Schraubenfeder ist gleich n·λ/2 (n = 1 oder 2 oder 3....). Für die Geschwindigkeit v einer Längswelle auf einer Feder mit der Federkonstanten D und der Masse m wurde hergeleitet: v = L·√(D / m)

f = v/ λ

↓

f = ( n·λ/2)· √(D / m) / λ = (n/2) ·√(D / m) → f_{Grundschwingung} = (1/2) ·√(D / m)

Eigenschwingungen in einer Pfeife

Von einer schwingenden Stimmgabel geht eine Folge von Luftverdichtungen und Luftverdünnungen aus (siehe Abb. 4). Der Luftdruck schwankt um den Normaldruck, wie dies durch das Diagramm in der Abb. 4 angezeigt wird.

Abb. 4

Zwischen zwei schwingenden Stimmgabeln gleicher Frequenz bildet sich eine stehende Schallwelle aus. Sie ist durch Bereiche mit großen Druckschwankungen Δp (Bäuche) und durch solche ohne Druckschwankungen ( Knoten) ausgezeichnet. Durch einen Knoten (Δp = 0) strömt fortwährend Luft zu einem Wellenbauch hin oder von einem Wellenbauch fort. Eine stehende Welle in einem Rohr bewirkt mit dieser Strömung, dass im Rohr verteiltes Korkmehl an den Druckbäuchen angehäuft wird (siehe Abb. 5).

Abb. 5: Kundtscher Versuch

Eigenschwingungen in der Form stehender Schallwellen werden in einer Pfeife erzeugt. Die Abb. 6 und 7 zeigen die Beschaffenheit einer Pfeife. Wir sehen einen hohlen Rundstab mit einem schrägen Einschnitt. Ein kleiner einseitig angeschliffener Zylinder ist in die runde Öffnung eingeschoben. Er verschließt diese Öffnung bis auf einen kleinen Schlitz. Wird in diesen Schlitz geblasen, dann strömt

Luft gegen den Rand A des schrägen Einschnitts ( siehe Abb. 8). Es bildet sich eine stehende Welle. Bei A ist ein Knoten der Druckschwankung und bei B ein Bauch. Die stehende Welle kann die Länge λ/4 oder 3· λ/4 oder 5· λ/4 …. haben. Die Länge L des Hohlraums ist somit ein ungerades Vielfaches von λ/4.

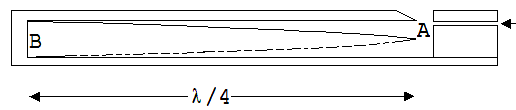
Abb. 8

Zum Verständnis muss gesagt werden, dass die Schallwelle bei B ohne Phasensprung vollständig und die zurück laufende Welle bei A mit einem Phasensprung teilweise reflektiert wird. Bei einer Eigenschwingung ist die Welle nach zweimaliger Reflexion an A und B so beschaffen als ob sie von A ausginge. Wegen des Phasensprungs ist dies dann der Fall, wenn die Zeit t für den Weg von A nach B und zurück T/2 oder T+T/2 oder 2· T +T/2 …. ist.

t = (2·n + 1)·T/2; n =0,1,2.....

t = (2·n + 1)·T/2; v = 2·L/t = λ/T → 2·L/[(2·n + 1)·T/2] = λ/T

↓

L=(2·n + 1)· λ/4

Der Luftstrom gegen die Kante A wird von der Strömung in der Welle abwechselnd nach außen und innen gelenkt (siehe Abb. 9). So erhält er die Eigenschwingung.

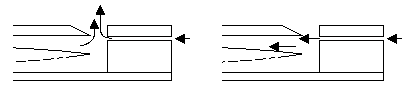
Abb. 9

Wenn nur ein einziger Druckbauch im Hohlraum der Länge L ist (Grundschwingung), dann gilt λ/4 = L.

↓

λ = 4 · L

v_Schall = λ · f ( f: Frequenz des Tons) → f = v_Schall / λ = v_Schall /( 4 · L)

L der oben abgebildeten Pfeife ist 9 cm.

L= 9 cm, v_Schall = 330 m/s

f = 330m/s / 0,36 m = 916 Hz