
Seilwelle

Abb. 1
In Abb. 1 ist ein Seil zu sehen, welches mit der Kraft F zwischen den Punkten A und B aufgespannt ist. Wird auf das eine Ende dieses Seils geschlagen, dann bildet sich eine Verformung aus, die sich selbständig zum anderen Ende hin mit einer Geschwindigkeit v ausbreitet. Was sich hier mit v bewegt, ist kein Teil des Seiles, sondern eine Zustandsänderung des Seils. Eine sich ausbreitende Zustandsänderung wird Welle genannt. In dem hier beschriebenen Fall spricht man von einer Seilwelle.Die Berechnung der Geschwindigkeit, mit der sich diese Seilwelle ausbreitet erscheint zunächst sehr schwierig.
Wie soll F= m·a angewandt werden ?
Eine Änderung in der Betrachtungsweise bringt bekanntlich oft völlig unerwartete Einsichten. Dies ist auch hier der Fall. Man muss mit den Augen eines Beobachters schauen, der die Verformung (Wellenberg) mit der Wellengeschwindigkeit v begleitet.
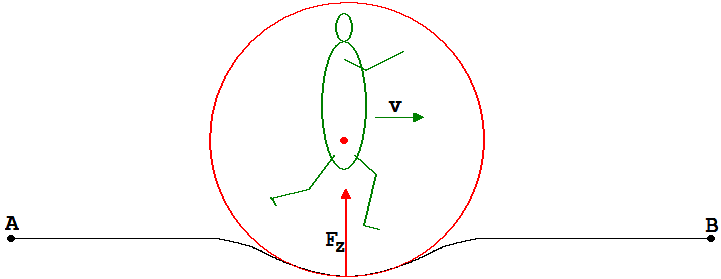
Abb. 2
Er sieht das Seil unter dem Einfluss von Zentralkräften FZ mit v durch einen Bogen fließen (Abb. 2).
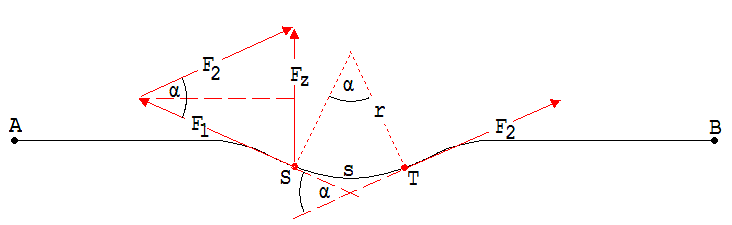
Abb. 3
Wir betrachten ein Bogenstück s aus dieser Seilwelle zwischen den Punkten S und T mit der Masse m (Abb. 3). Die Zentripetalkraft Fz = m·v2 /r auf dieses Bogenstück ist die Resultierende der bei S und T angreifenden Fadenzugkräfte F1 und F2 mit übereinstimmenden Beträgen F. r ist der sogenannte Krümmungsradius von s, hierunter verstehen wir den Radius des Kreises, der dem Bogenstück s angepasst werden kann.
Fz/2 = F· sin(α / 2) → Fz = 2·F· sin(α /2) → m·v2/r = 2·F· sin(α /2)
m/s = σ (σ = längenbezogene Dichte) → m = s·σ
s = α·r (α = Winkel im Bogenmaß) → m = α ·r ·σ
Setzt man α ·r ·σ für m in 2·F· sin(α /2) = m·v2 /r ein, dann gelangt man zu:
2·F· sin(α /2) = α·r·σ·v2/r → 2·F· sin(α /2) = α·σ·v2
Bei kleinen Winkeln α kann geschrieben werden: sin(α /2) = α /2
2·F· sin(α /2) = α·σ·v2 → 2·F· α /2 = α·σ·v2 → F = σ ·v2 → v = √(F/ σ)
Messung der Wellengeschwindgkeit
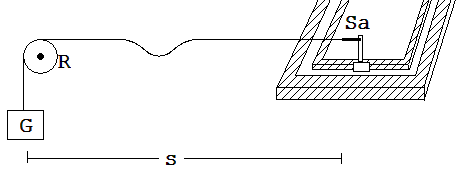
Abb. 4
Ein dünnes Seil ist zwischen einem Scharnier Sa an der Experimentierwippe und einer um s = 5 m entfernten Rolle aufgespannt (siehe Abb. 4). Das angehängte Gewicht sorgt für eine bestimmte Zugkraft F. Mit einem kurzen Schlag auf das Seil entsteht eine Welle, die zwischen R und Sa mehrfach hin und her reflektiert wird. Die Erschütterung, welche die Wippe bei einer Reflexion erfährt, wird von einem Rechner registriert. Die Zeitdifferenz t zwischen zwei aufeinander folgenden Erschütterungen ist die Laufzeit einer Welle entlang einer 10 m langen Strecke. 2·s/t = Wellengeschwindigkeit.
Federwelle
Eine lange Schraubenfeder der Länge L und der Masse m ist unter der Zugkraft F zwischen einer Wand und der Hand eines Schülers aufgespannt. Ein Schüler zieht plötzlich ruckartig am rechten Ende der Feder und erzeugt damit nahe seiner Hand einen stärker gedehnten Bereich B, der sich anschließend mit einer Geschwindigkeit v nach links über die gesamte Feder bewegt (siehe Abb. 5).

Abb. 5
Wünscht man eine Gleichung für die Wellengeschwindigkeit v, dann sollte man wie im Fall der Seilwelle zum besseren Verständnis mit den Augen eines Beobachters schauen, der B mit v begleitet. Aus seiner Sicht wandert eine Windung nach der anderen von links mit der Geschwindigkeit v in B hinein. Die einzelnen Windungen mit der Anfangslänge Lʼ und der Masse mʼ werden gedehnt, was zu einer Beschleunigung ihrer Schwerpunkte führt. Schließlich nimmt die Dehnung der Windungen wieder ab. Die Schwerpunkte werden auf die Geschwindigkeit v gebremst (siehe Abb.6).
|
Abb. 6 |
Abb. 7 |
Wir betrachten von links die ersten n Windungen im Bereich B. Wir denken uns diese von links nach rechts nummeriert. Die Nummer 1 ist gerade in B mit der Wellengeschwindigkeit v = L'/ Δt eingetreten. Auf die Windungen von 1 bis n (siehe Abb.7) wirkt insgesamt die Kraft Fn - F = mʼ·an +mʼ·an-1 + …..+mʼ·a2 + mʼ·a1 = mʼ·(an + an-1 + ….. + a2 + a1 ). F und Fn sind die Zugkräfte an der 1. und n. Windung.
Die Zugkraft auf die n. Windung ist nach dem Eintritt in den Bereich B von anfänglich F auf Fn angestiegen. Fn – F = mʼ·(an + an-1 + …..+ a2 + a1 ) ist die Zunahme ihrer Federkraft. Nach dem Federgesetz hat diese Windung somit in B eine Dehnung um ΔLʼ= (Fn – F) / Dʼ = mʼ·(an + an-1 + …..+ a2 + a1 ) / Dʼ erfahren. Dʼ ist die Federkonstante einer Windung.
Wenn in der Zeit Δt von links eine Windung mit der Geschwindigkeit v = L'/Δt in B hineingezogen wird, dann tritt an die Stelle der n.Windung die n-1. Windung und verschiebt dabei die n. Windung um Lʼ + ΔLʼ. Die zuvor n. Windung hat dann die Geschwindigkeit (Lʼ + ΔLʼ) / Δt = v + ΔL' / Δt. Somit wurde ihre Geschwindigkeit in B um ΔLʼ/Δt vergrößert.
ΔLʼ/Δt = [ Fn – F) / Dʼ ] / Δt = [mʼ·(an +an-1 + …..+a2 + a1 )/Dʼ]/ Δt
Diese Geschwindigkeitsänderung kann auch auf andere Art berechnet werden:
Die n. Windung hat als 1., 2. , 3. , ...n. Windung die Geschwindigkeitszuwächse a1· Δt, a2· Δt, a3· Δt, …... erfahren.
ΔLʼ/Δt = a1· Δt + a2· Δt + a3· Δt +...........+ an· Δt = Δt·(an +an-1 + …..+a2 + a1 )
↓
mʼ·[(an +an-1 + …..+a2 + a1 )/Dʼ] /Δt = Δt·(an +an-1 + …..+a2 + a1 )
↓
mʼ/Dʼ = Δt2 → v = Lʼ/ Δt = Lʼ · √(Dʼ/mʼ)
Dʼ und mʼ können anhand der Masse m und der Federkonstanten D der gesamten Feder berechnet werden. j sei die Zahl der Federwindungen.
m = j·mʼ → mʼ = m / j
Ist eine Windung um ΔLʼ gedehnt, dann ist die gesamte Feder bei gleichmäßiger Dehnung um j · ΔLʼ verlängert. Die Kraft einer Windung gleich der Kraft der gesamten Feder.
D·(j·ΔLʼ) = Dʼ·ΔLʼ → Dʼ = j·D
↓
v = Lʼ·√[D·j / (m / j)] = Lʼ·√(D·j2 / m) = j·Lʼ· √(D / m); j·Lʼ ist die Federlänge L
↓
v = L· √(D / m)
Einen Wellenträger können wir gedanklich in viele Abschnitte gleicher Masse einteilen und jedem dieser Abschnitte eine beschleunigende Kraft F zuordnen. Nach der Richtung von F unterscheidet man Längs- und Querwellen. Ist F wie bei der Federwelle parallel zur Ausbreitungsrichtung, dann spricht man von einer Längswelle (Longitudinalwelle) , andernfalls, z.B. im Fall der Seilwelle, von einer Querwelle (Transversalwelle). Die Kräfte F bilden ein Kraftfeld.