1.12.7   Kreisel und Kreiselkompass

1. Der Kreisel

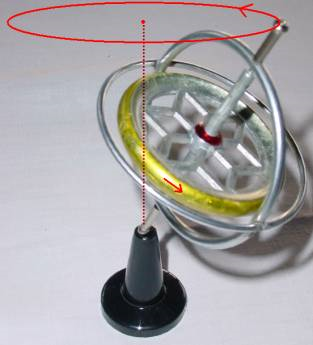
Unter einem Kreisel versteht man einen starren Körper, der um einen Punkt frei beweglich ist. Wird ein Kreisel in Schräglage in eine schnelle Drehung versetzt (siehe Abb. 1), dann dreht sich die Kreiselachse so, dass sie einen Kegelmantel beschreibt. Diese Bewegung heißt Präzession der Kreiselachse („praecedere“ (lat.) = das Vorangehen).

Abb. 1

Mit „192“ und „START“ erfolgt eine Vorführung !

Zur Erklärung dieser Erscheinung dient die Abb. 2 Der rotierende Zylinder hat den Drehimpuls L, der während eines kleinen Zeitabschnitts Δt um ΔL geändert wird. ΔL/Δt zeigt das nach unten wirkende Drehmoment m·g·r der Gewichtskraft an. Der Kreisel wirkt mit einem dem Betrage nach gleich großen Gegenmoment der Gewichtskraft entgegen und hält somit seinen Schwerpunkt auf der in der Abb. 2 angedeuteten Kreisbahn (Radius r).

Die Umlauffrequenz des Kreiselschwerpunkts heißt Präzessionsfrequenz f, ω’ ist die zugehörige Kreisfrequenz. Mit Blick auf die Abb. 2 findet man sehr schnell zu einer Gleichung für ω’.

Die Geschwindigkeit |ΔL|/ Δt, mit der sich die Vektorspitze von L bewegt, verhält sich zur Geschwindigkeit ω’ · r des Schwerpunkts S so wie |L| zu d (Strahlensatz).

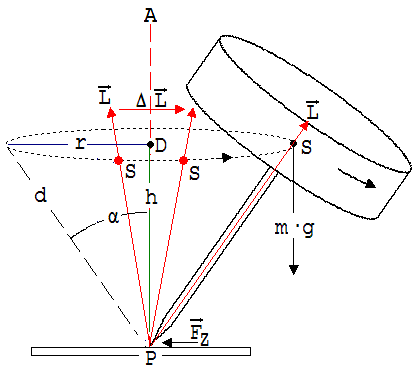
Abb. 2

(|ΔL|/ Δt)/ (ω’· r) = |L|/ d → |ΔL|/ Δt = |L| · ω’ · r/ d

|ΔL|/ Δt ist gleich dem Drehmoment m· g · r

P ist der Bezugspunkt für die Drehimpulse und Drehmomente, somit ist das zur Zentralkraft F_Z gehörende Drehmoment gleich 0 !

m· g · r = |L| · ω’ · r/ d → m· g · d = |L|· ω’; |L| = J · ω

ω ist die Winkelgeschwindigkeit des Zylinders um die präzedierende Achse.

↓

ω’ = m· g · d / (ω ·J) → f = ω’ /(2· π) = m· g · d / (ω ·J· 2 · π)

↓

f nimmt mit abnehmendem ω zu.

Das hier gewonnene Ergebnis ist nur annähernd richtig. Es beschreibt den Sachverhalt nur dann zufriedenstellend, wenn ω’ sehr klein gegenüber ω ist, denn der Drehung der Figurenachse ist auch ein Drehimpuls L' mit einer waagrechten Komponenten zuzuordnen. Diese Komponente dreht sich mit ω’, erfährt demzufolge eine Änderung, für welche das Drehmoment m· g · d verantwortlich ist. Bei waagrechter Lage der Figurenachse ist L' ein senkrecht nach oben gerichteter konstanter Vektor, weshalb ihm kein Drehmoment zugeordnet werden kann. In diesem Fall gilt die für f angegebene Gleichung genau.

Abb. 3

In Abb. 3 ist ein Kreisel mit waagrechter Rotationsachse zu sehen. Es handelt sich um den schon mehrfach erwähnten Pendelkreisel. Hier ist dieses Pendel an einem durch seinen Schwerpunkt geführten, waagrechten Rundstab aufgehängt. Die tragenden Fäden laufen nach oben hin zusammen. Wird am Pendel mit rotierendem Zylinder im Abstand d vom Schwerpunkt ein Gewicht mit der Masse m angehängt, dann dreht sich das Pendel um eine senkrechte Achse mit

ω’ = m· g · d / (ω ·J) .

Mit Versuchsanordnung der Abb. 3 können noch 2 andere interessante Phänomene gezeigt werden:

1. Die Nutation, hierunter versteht man die Kreiselbewegung, die durch einen Stoß veranlasst wird. Stößt man auf die Rückseite des in der Abb. 3 sichtbaren Kreisels, dann erhält der Zylinder zu dem vorhandenen Drehimpuls L_Z einen Zusatzimpuls L_S (siehe Abb. 4). Wirkt kein Drehmoment am Kreisel, dann bleibt der neu gewonnene Drehimpuls L (Impulssumme) konstant. Um ihn kreist nun der Drehimpuls L_Z des Zylinders und beschreibt hierbei einen Kegelmantel (Nutationskegel).

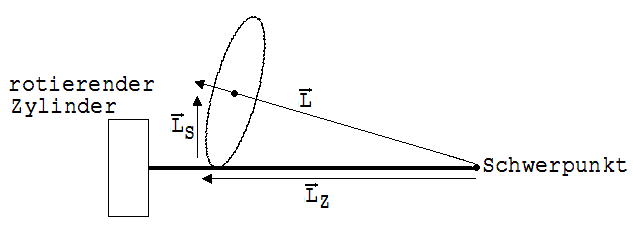
Abb. 4

2. Schwenkt man das Pendel ohne angehängtes Gewicht mit den Haltefäden hin und her, dann behält die Rotationsachse ihre Richtung. Hiermit wird deutlich, wie durch den Drehimpuls eine Richtung stabilisiert wird. So wird verständlich, dass ein rollendes Rad weniger zum Umfallen neigt als ein stehendes.

2. Der Kreiselkompass

In Abb. 5 und 6 ist der Pendelkreisel auf einer rotierenden Scheibe S zu sehen. Der durch seinen Schwerpunkt geführte Rundstab R ist in S drehbar gelagert. Während der Scheibenrotation dreht sich der Pendelkreisel um R, bis seine Rotationsachse parallel zur Scheibenachse ist.

Zur Erklärung dieses Verhaltens dient die Abb. 7. Wir setzen voraus, dass der Pendelkreisel an einer Drehung um R gehindert werde. In diesem Fall erfährt er die Drehimpulsänderung ΔL, die durch ein Drehmoment verursacht wird, welches den Pendelkreises an einer Drehung nach vorne hindert. Ohne Behinderung erfolgt demnach diese Drehung.

Der Pendelkreisel auf der rotierenden Scheibe ist mit einem Kreiselkompass auf der rotierenden Erde vergleichbar. Kernstück des Kreiselkompasses ist ein um eine waagrechte Achse rotierender Zylinder. Die waagrechte Achse kann sich um eine senkrechte Achse drehen. Ist die waagrechte Achse zunächst von Osten nach Westen gerichtet, dann dreht sie sich während der Drehung der Erde in eine Meridianebene.