1.12.1 Der Drehimpuls und Drehimpulssatz
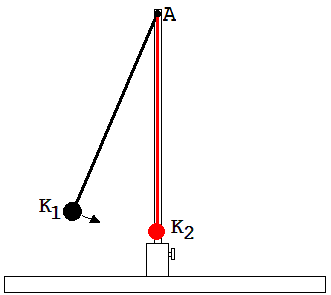
Ein Stativstab auf der Mitte der Experimentierwippe hält an einer waagrechten Achse A eine Kugel K2 der Masse m2 . Sie kann sich an einem leichten Stab S (rot) um A drehen. Stößt eine andere Pendelkugel K1 auf K2 (siehe Abb.1), dann ändert sich die Summe aus den Impulsen der beiden Kugeln während des Stoßes nicht.
Schlussfolgerung: Der Stativstab erfährt während dieses Ereignisses keine Kraft, die Kraft von K1 wird völlig auf K2 übertragen.


Abb.1 Abb.2
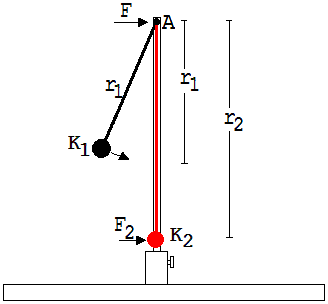
Schlägt K1 nicht auf K2 , sondern stattdessen auf den Pendelstab S mit der Kraft F1 ein (siehe Abb. 2), dann wirkt während des Stoßes eine Kraft F, ein Teil der Kraft F1 , auf die Achse A .
Schlussfolgerung: Im Zweiten Fall wirkt auf K2 eine Kraft F2 < F1 .
Dies kann mit Hinweis auf das Hebelgesetz leicht begründet werden, denn nach diesem Gesetz gilt: Wirkt auf einen Hebel im Abstand r1 vom Drehpunkt eine Kraft F1, dann übt der Hebel auf einen Körper im Abstand r2 vom Drehpunkt die Kraft F2=( r1/r2 ) · F aus.
F2 · r2 = F1 · r1 : Hebelgesetz
Was für die Kraft gilt, trifft auch für die Impulsänderungen während des Stoßes zu.
-F1 (Gegenkraft zu F1) ändert den Impuls von K1 nach -F1 = Δ(m1·v1)/ Δt und F2 den von K2 nach F2= Δ(m2·v2)/ Δt.
F1 · r1 = F2 · r2 → (-Δ(m1·v1)/ Δt) · r1 = (Δ(m2·v2)/ Δt) · r2
↓
- Δ(m1 ·v1 ) ·r1 = Δ(m2 · v2 ) · r2 → Δ(m2 · v2 ) · r2 + Δ(m1 ·v1 ) · r1 = 0
F1 , F2 , m1 ·v1 und m2 · v2 sind Kräfte und Impulse quer zum Stab. Wir vereinbaren, dass diese Größen ein positives Vorzeichen haben sollen, wenn sie zu einer Linksdrehung gehören oder im Sinne einer Linksdrehung wirken. Andernfalls sollen sie negativ sein.
Das zu einem Massepunkt gehörende Produkt m·v·r nennen wir Drehimpuls L ( v = Geschwindigkeitskomponente senkrecht zu r).
Wir vermuten: Die Summe der Drehimpulse L aller Teile eines abgeschlossenen Systems bleibt konstant (Drehimpulssatz).
Für diese Vermutung spricht auch das Ergebnis des folgenden Gedankenexperiments:
Wir lassen eine Kugel K in Gedanken reibungsfrei in einer sehr leichten, dünnwandigen Röhre gleiten, die sich um eine senkrechte Achse D reibungsfrei drehen kann (siehe Abb.3). Die Kugel bewegt sich nach dem Trägheitssatz gleichförmig und führt hierbei die Röhre mit sich, deren Masse vernachlässigbar klein ist.
|
Abb. 3 |
m·v / m ·vq = r2 / r1 ähnliche Dreiecke! ↓ r1 · m·v = r2 · m ·vq r · m ·vq ändert sich nicht ! |
Hier ist von einem Drehimpuls eines fast völlig freien Teilchens die Rede. Dieses Beispiel gibt Anlass zur Definition eines Drehimpulses für jedes beliebige Teilchen P.
Wir denken uns ein Teilchen P, welches im Augenblick den Impuls p hat, und von einem Ortsvektor r angezeigt wird, der von einem beliebig gewählten Punkt D ausgeht. P kann frei beweglich sein.
Unter dem Drehimpuls L von p verstehen wird das Produkt mit dem Betrag |r| ·|pq|. pq ist die Komponente von p senkrecht zu r in der von r und p aufgespannten Ebene (siehe Abb. 4). L hat im Fall einer Linksdrehung ein positives und andernfalls ein negatives Vorzeichen.
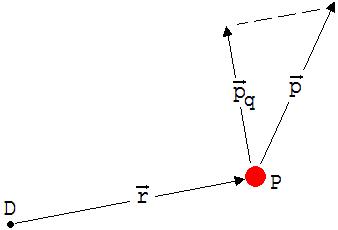
Abb. 4
Drehimpulsvektor
L erscheint zur Beschreibung des Drehimpulses nicht ausreichend. Es wird eine Angabe über die Lage der Geraden (Drehachse) vermisst, um die sich der Vektor r dreht. Diese Gerade (Achse) steht senkrecht zu der durch r und p aufgespannten Ebene. Zur Beschreibung von L und der Achsenlage definieren wir einen Drehimpulsvektor L mit folgenden Eigenschaften (siehe Abb. 5):
|L| = |L| . L steht senkrecht auf der durch r und p aufgespannten Ebene. Bei einer Linksdrehung ist L auf den Betrachter gerichtet.
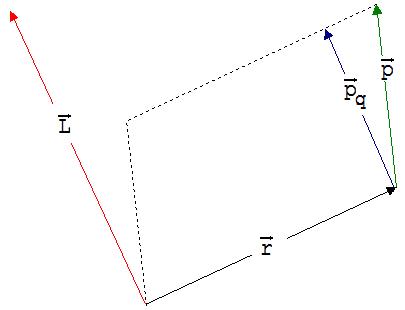
Abb. 5
Eine Methode zur Bestimmung von L kann sofort angegeben werden. L gleicht dem Kreuzprodukt r x p (siehe Kapitel Flächengeschwindigkeit).
L = r x p
Von nun an verstehen wir unter dem Drehimpuls nur noch den hier angegebenen Vektor L.
Für die Vektoren L gilt der oben angegebene Drehimpulssatz.
Beweis:
Wir denken uns ein abgeschlossenes System mit Teilchen der Impulse p1, p2, p3, p4 ....... und den Ortsvektoren r1, r2, r3, r4........ in Bezug auf einen Drehpunkt D.
Nach dem Drehimpulssatz gilt:
r1 x p1 + r2 x p2 +r3 x p3 +r4 x p4 +... =konstanter Vektor Lg
Aus der Konstanz der Vektorsumme folgt:
d Lg / dt = d( r1 x p1 + r2 x p2 +r3 x p3 +r4 x p4 +...)/ dt =0
d Lg / dt = (d r1 /dt x p1 + r1 x dp1/dt) + (d r2 /dt x p2 + r2 x dp2 /dt) + (d r3 /dt x p3 +
r3 x dp3/dt ) + (d r4 / dt x p4 + r4 x dp4/dt ) +...=0
Produktregel der Differentialrechnung !
d Lg / dt = (v1 x p1 + r1 x dp1/dt) + (v2 x p2 + r2 x dp2 /dt) + (v3 x p3 + r3 x dp3/dt ) +
(v4 x p4 + r4 x dp4/dt ) +...=0
Die Kreuzprodukte v x p sind Nullvektoren, weil v und p = m·v gleiche Richtungen haben.
d Lg / dt = (r1 x dp1/dt) + ( r2 x dp2 /dt) + ( r3 x dp3/dt ) + ( r4 x dp4/dt ) +...=0
dp1/dt, dp2 /dt, dp3/dt, dp4/dt .. sind die auf die Teilchen 1, 2, 3, 4.. wirkenden Kräfte F1 , F2 , F3 , F4 …
d Lg / dt = (r1 x F1) + ( r2 x F2) + ( r3 x F3 ) + ( r4 x F4 ) +...=0
Die letzte Gleichung kann mit Hilfe des Wechselwirkungsgesetzes bewiesen werden.
Zu jeder Kraft Fi,j eines Teilchens i auf ein Teilchen j gehört eine Gegenkraft Fj,i eines Teilchens j auf ein Teilchen i.
Fi,j = - Fj,i
rj x Fi,j +ri x Fj,i = ( rj - ri ) x Fi,j
Für Kreuzprodukte gilt auch das Distributivgesetz !
( rj - ri ) ist parallel zur Verbindungsstrecke zwischen den Teilchen i und j. Wird vorausgesetzt, dass die Kraft Fi,j parallel zur genannten Verbindungsstrecke verläuft, dann gilt:( rj - ri ) x Fi,j = 0.
Da (r1 x F1) + ( r2 x F2) + ( r3 x F3 ) + ( r4 x F4 ) +.. als eine Summe von Termen der Art ( rj - ri ) x Fi,j dargestellt werden kann und die Voraussetzung Fi,j || rj - ri den allgemeinen Erfahrungen entspricht , ist für ein abgeschlossenes System die Schlußfolgerung d Lg / dt = 0 → Lg = konstanter Vektor berechtigt
Nach dem Eintrag von „165“ und „START“ erscheint ein Programm zur Berechnung eines Kreuzproduktes.