Glasfahrbahn (Experimentierwippe) -

Ladungs-, Leistungs- und Energiemessung

F. Höhne

Mit der Glasfahrbahn nach G. Höhne können wichtige elektrische Größen auf einfache und anschauliche Weise gemessen werden (Abiturfacharbeit).

1. Ladungsmessung

1.1 Messung mit einem Ballistischen Galvanometer

1.1.1 Prinzip der Ladungsmessung

Mit Hilfe der Fahrbahn kann man leicht ein Ballistisches Galvanometer verwirklichen, das zur Ladungsmessung geeignet ist. Unter einem Ballistischen Galvanometer versteht man ein träges Galvanometer (Drehspulinstrument) mit geringer Dämpfung. Die Trägheit ist so groß, dass es bei einem kurzzeitigen Durchlauf elektrischer Ladungen (Stromstoß) fast nicht aus der Ruhelage gedreht wird. Der Stromstoß erteilt einen Impuls, der anschließend zu einem registrierbaren Ausschlag führt.

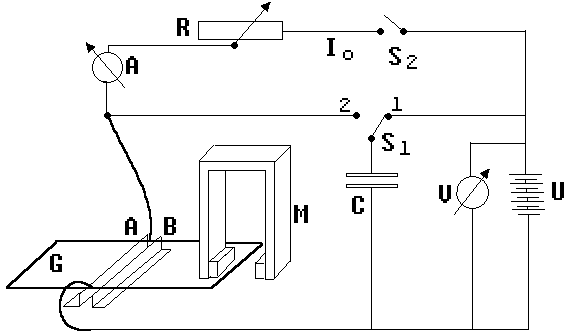
Abb.1: Versuchsanordnung zur Ladungsmessung

1.1.2 Versuchsaufbau

In einem vorangehenden Aufsatz von G. Höhne wird die Messung kleiner Kräfte mit Hilfe der Glasfahrbahn beschrieben. Auf die dort genannten Schienen E und H (hier A und B) wird nun ein mit Kupferdraht umwickelter Rahmen der Maße 20 cm ·7 cm gelegt (1550 Windungen; Durchmesser des Kupferdrahts 0,2 mm). Um die über die Fahrbahn hinausragende Schmalseite dieses Rahmens wird ein Hufeisenmagnet gestellt, dessen Polabstand man zur Verstärkung der magnetischen Feldstärke mit kleinen Magneten verkleinert. Hierbei ist Vorsicht geboten, denn der Rahmen muß noch frei schwingen können.

1.1.3 Versuchsdurchführung

Wie in der Abb. 1 angedeutet, wird ein Kondensator C mit einer bestimmten Spannung U aufgeladen. Schalter S₁ befindet sich zunächst in Stellung 1. Anschließend legt man den Schalter in Stellung 2 und entlädt den Kondensator über das Ballistische Galvanometer G. Der an die Fahrbahn angeschlossene  t-y-Schreiber zeichnet hierbei das Diagramm ( siehe Abb. 2) einer gedämpften Schwingung.

Abb. 2: Darstellung der gedämpften Schwingung

1.1.4 Versuchsauswertung

Zeichnerische Extrapolation (siehe Abb. 2) ergibt die Amplitude A, die sich ohne Dämpfung einstellen würde.

Wie kann nun anhand der Amplitude A auf die Ladung Q des Kondensators C geschlossen werden?

Es muss die Stromstärke I_o ermittelt werden, bei der sich der Ausschlag A einstellt. Zu diesem Zweck lässt man einen Strom I < 0,3 mA (Schalter S₂) durch die Apparatur fließen und misst die zugehörende Verschiebung A' des Messzeigers. Die Verhältnisgleichung I/A' = I_o/A ermöglicht die Berechnung von I_o.

Die Ladung Q erhält man nach der Gleichung: Q = I_o/ω ;   ω = Kreisfrequenz der Schwingung

 Vorsicht!

Die Stromstärke I darf nicht ruckartig verändert werden, da bei einem derartigen Vorgang der Rahmen geringfügig verschoben wird und so Messfehler entstehen.

1.1.4.1 Herleitung der Gleichung Q = I_o/ω

Damit diese Gleichung mit den schulüblichen Kenntnissen der Mechanik hergeleitet werden kann, wird die Versuchsanordnung in Gedanken abgewandelt. Nach Abb. 3 hängt der Rahmen an einer Spiralfeder zwischen. den Polen eines Hufeisenmagneten.

Abb. 3: Zur Herleitung der Beziehung Q = I_o/ω

Eine Kondensatorentladung verursacht einen kurzzeitigen Kraftstoß und erteilt damit dem Rahmen einen Impuls p = m·v_o, je nach Polung nach oben oder nach unten. Der Rahmen beginnt zu schwingen. Für die Elongation der Schwingungen gilt s =A·sin(ω·t).  Mit der ersten Ableitung erhält man v:       v = A · ω ·cos(ω·t)

Hieraus ergibt sich für die Geschwindigkeit beim Durchgang der Ruhelage ( cos (ω ·t)=1):    v_o = A· ω

Die Kraft F ist proportional der Stromstärke I und so gilt:    F = dp/dt = k·I ; k: Proportionalitätskonstante

Mit I = dQ/dt (Q: fließende Ladung) folgt: dp/dt = k·dQ/dt

Nach Integration beider Seiten ergibt sich: p = k·Q

Aus p = v_o·m und v_o = A·ω und Q = p/k folgt:   Q = v_o·m/k ;   Q = A·ω·m/k

Mit ω² = D/m     çè      m = D/ω² erhalten wir: Q = A·D/(k·ω) (1)

A·D beschreibt die Kraft, die erforderlich ist, den Rahmen um A aus der Ruhelage zu ziehen.

Bestimmung der Proportionalitätskonstanten k:

In Gedanken fließt ein Strom I_o durch den Rahmen und bewirkt den Ausschlag A.

F = D·A = k·I_o     è    k = D·A/I_o   in Gleichung (1)     è  Q = I_o/ω        q.e.d.

1.1.4.2 Meßergebnisse

Der Versuchsaufbau der Abb. 1 enthält einen 4μF-Kondensator, der nacheinander mit den Spannungen U1 = 2,5 V,   U2 = 5V und   U3 = 7,5 V aufgeladen wird. Die Auswertung der Meßdiagramme liefert die Ergebnisse der nachfolgenden Tabelle.

 Messergebnisse

Zur Prüfung der Meßgenauigkeit bildet man aus den zu 5 V gehörenden Werte den mittleren Fehler des Mittelwerts nach der Gleichung:

n: Zahl der Messwerte;       σ =0,01·10^-5 C ;     Q_5V = (1,86 ± 0,01)·10^-5 C

Dies sagt aus, dass der wahre Wert der Ladung Q mit 68 % Wahrscheinlichkeit in den angegebenen Messbereich (1,86  ±0,01)·10^-5 C fällt.

Nach der Gleichung C = Q/U wird die Kapazität berechnet. An der Tabelle kann die Proportionalität Q~U abgelesen werden.

C = 3,9 μF

Die Schwankungen der Kapazitätswerte beruhen hauptsächlich auf Ungenauigkeiten bei der Einstellung der Spannungsquelle. Die statistischen Fehler sind im Vergleich dazu geringfügig.

1.1.5 Ein weiteres Beispiel zur Ladungsmessung mit einem Ballistischen Galvanometer

1.1.5.1 Bestimmung von ε₀

Für die Kapazität eines Plattenkondensators gilt:   C = ε_o·ε_r·A/d;      ε_r (Luft ) ≈ 1     è     ε_o = C·d/A

Zur Ermittlung von ε_o dient ein Plattenkondensator d mit A = 510 cm² und d = 1 mm, der mit 1000V aufgeladen wird. Da das Galvanometer in diesem Fall auf die Ladung  nur geringfügig anspricht, werden zunächst etwa 20 Plattenkondensatorladungen auf einen 4μF-Kondensator C₂ gebracht. Anschließend entlädt man C₂ über das Ballistische Galvanometer (siehe Abb. 4).

Wenn man es genau nimmt, dann muß man feststellen, daß die Ladung des Plattenkondensators nicht vollständig zum 4μF-Kondensator fließt. Sie verteilt sich auf beide Kondensatoren. Bedenkt man jedoch (die Messung zeigt es), daß die Spannung am Plattenkondensator während der Entladung auf U ≤ 2V herabsinkt, dann kann man sagen, daß mindestens 99,8 % der Ladung an den 4μF-Kondensator abgegeben wird.

Mit dieser Meßanordnung ergaben sich für 20 Plattenkondensatorladungen (Messung wie in 1.1.1)

20 ·Q = 8,8·10^-6 C   è    Q = 4,4·10^-7 C   è   C = 4,4·10^-10 F

ε_o = 4,4·10^-10 F·1mm / 510 cm²   =   8,6·10^-12 F/m

Abb. 4: Versuchsanordnung zur Bestimmung von ε_o

1.2 Ladungsmessung im Kondensatorfeld

Abb. 5: Zur Bestimmung der Ladung auf einer Styroporkugel

Welche Ladung befindet sich auf einer ungeriebenen Styroporkugel?  Zur Beantwortung dieser Frage benutzt man den in Abb. 5 skizzierten Versuchsaufbau. Eine Styroporkugel K (Durchmesser = 6 cm) befindet sich zwischen den Platten eines Kondensators (Plattenfläche A = 20·20 cm² Abstand d =13 cm), an denen die Spannung U = 10kV während des Versuchs anliegt. Die Kugel ist am Ende eines Waagebalkens befestigt, der auf den schon mehrfach genannten Schienen A und B aufliegt. Das rechter Hand aufgelegte Gewicht dient zum Ausbalancieren des Waagebalkens. Wird die Spannungsquelle von 0 auf 10 KV eingestellt, zeichnet der  t-y-Schreiber einen 5,3 cm großen Ausschlag.

Zur Bestimmung der zugehörenden, auf die Kugel wirkenden Kraft legt man anschließend ein 50 mg-Gewicht ( 4,9·10^-4N) auf den Styroporkörper. (Ausschlag = 3,4 cm). So kann über einen Dreisatz die Kraft berechnet werden, die zu dem Ausschlag von 5,3 cm führt:

F = (4,9·10^-4 N / 3,4 cm)·5,3 cm = 7,6·10^-4 N.

Bekanntlich kann die Kraft im Kondensatorfeld (homogenes Feld!) über die Gleichung F = E · Q berechnet werden.

Unter Berücksichtigung von E = U/d ergibt sich für die Ladung Q:   Q = F·d/U = 9,9·10 ^{- 9} C

Welche Ladung hat eine geriebene Kugel?

Die Styroporkugel wird kurz mit einem Wolltuch gerieben und anschließend in das Kondensatorfeld gebracht. Nun wird unter den zuvor beschriebenen Bedingungen ein Ausschlag von 14,4 cm registriert. Dies entspricht der Ladung 2,7·10^-8 C. Die Ladung ist somit auf den fast dreifachen Wert angestiegen.

Ergänzung:

Ein weiterer Versuch dient zur Prüfung, inwieweit der Zeigerausschlag S des Schreibers der Kondensatorspannung U proportional ist. Die Messwerte sind in der folgenden Tabelle zusammengestellt.

Die Tabelle verdeutlicht: S ~ U

Die Abweichungen von S ~ U sind auf ungenaue Anzeige des Hochspannungsmeßgerätes zurückzuführen.

2. Leistungs- und Energiemessung

2.1 Leistungsmessung

2.1.1 Gleichstromkreis

2.1.1.1 Versuchsaufbau

Abb. 6: Versuchsanordnung zur Messung der elektrischen Leistung

Abb. 6 zeigt ein Wattmeter; mit diesem Versuchsaufbau wird die elektrische Leistung im Widerstand R und der Spule Sp gemessen. 1,8 Ω ·I ² und 277Ω·I ²  sind die Leistungen in  der Spule und im Verbraucher R, welcher mit der Spule in Serie geschaltet ist. Die zuerst genannte Leistung ist im Vergleich zur Leistung des Verbrauchers  R vernachlässigbar klein. Der Rahmen wird hier nicht von einem Hufeisenmagneten, sondern von der Spule S_p abgelenkt; er nimmt wegen seines relativ hohen Widerstandes wenig Energie auf.

2.1.1.2 Versuchsauswertung und Meßergebnisse

Für die Kraft auf den Rahmen G gilt:    F  ~   I_Sp·I_G

Unter Berücksichtigung von I_G ~ U folgt:      F  ~  I_Sp· U   è      F   ~   P

I_Sp: Strom durch R und Sp

I_G: Strom durch den Rahmen G

U: Spannung über R und Sp

P: In R (277Ω ) und Sp (l,8 Ω) verbrauchte Leistung

Zunächst wird S ~ P überprüft (S: Ausschlag des Schreibers ).

Hiermit ist die Proportionalität bestätigt.

Dem Ausschlag von 11,35 cm entspricht die Leistung: P = I² · R_ges;   P = 0,01 A² · 279 Ω  = 2,79 W

R_ges = R + R_Sp= 277 Ω + 1,8 Ω

2.2 Energiemessung

Abb. 7: Versuchsanordnung zur Bestimmung der elektrischen Energie

Entsprechend der Abb. 7 wird ein 40μF-Kondensator, der zuvor mit 100 V aufgeladen wurde, über das Wattmeter entladen. Hierbei zeichnet der Rechner eine gedämpfte Schwingung auf. Anhand des Diagramms kann man wieder auf die Amplitude A extrapolieren, die bei einer Schwingung ohne Dämpfung erreicht würde. A ist der bei der Entladung frei werdenden Energie proportional.

Die Energie erhält man nach: E = P_o/ω.

P_o: Leistung, die zu dem Ausschlag A führt.

Die Herleitung von E = P_o/ω. gleicht der von Q = I_o/ω. die bereits im Kapitel 1.1.4.1 beschrieben wurde. E und P_o entsprechen Q und I_o. In dem angedeuteten Experiment wird auf diese Weise E = 0,23 J gemessen. Der theoretische Wert ist bekanntlich E  =  U²·C/2 = 0,2 J.

Veröffentlichung in der Praxis der Physik PdN-Ph. 2/39. Jg. 1990