
Mechanics with the Measuring-Seesaw
by Gerhard Höhne
Preface
The Law of conservation of momentum should be known, if the concept of „Force” is introduced in Physics. Starting from this law, the definition F = d(m ·v) / dt seems to be logical and it can be explained convincingly that Δ (m · v) is a suitable measure for an outer influence. Hence, a measuring instrument is desired, which facilitates experiments to demonstrate the conservation of momentum.
The Measuring-Seesaw developed by myself is a device with the desired qualities. It is a very versatile instrument to measure displacements, forces, and torques.
Working with this instrument, I could see that pupils propose new experiments again and again and the lesson continuously proceeds.
In the following chapters the operation of the Measuring -Seesaw will be explained first and then some few applications of this instrument in lessons are described . E.g. it is shown how to introduce the “Force”.
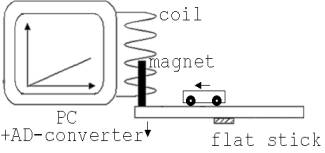
1. Construction and operation of the Measuring-Seesaw


Fig. 1
A framed glass-disk is screwed in its middle to an aluminum flat stick which is carried by an aluminum frame (Fig.1)
If e.g. a little wagon (m < 0.15 kg) rolls over the disk, then it is turned a little (<0,1°, frequency of the disk = 10 s-1) proportionally to the way of the wagon. The marginal turn cannot significantly influence the movement.
To measure this turn there ist a coil with 8000 windings at the outer frame hidden in a box. A very strong, little stick-magnet, which is fastened at the mobile seesaw, is inserted into this coil. If the seesaw is turned (less than 0.1 °), then the magnet causes an induction voltage U and a charge is going through the cross-section of the wire proportionally to the turn of the disk. This charge is measured with a PC + AD-converter. Appropriate systems are available at schools (Leybold, Phywe and Pasco..).
With these programs , belonging to the AD-converter, the integral of the induction voltage can be calculated. This integral is proportional to the charge.
If the pupils don't know the word integral yet, then the word charge should be used instead to explain the measuring principle. Although the input voltage is 0 , the AD-converter transmits a small value to the computer. To compensate this fault, a small value ε must be added to the output-value of the AD-converter. If fitting of a suitable ε seems too difficult, the voltage-integration should be done electronically. An exact integrator has to be created easily with a chopper operation amplifier (Texas - Instruments).
If someone compares the Measuring-Seesaw with similar measuring-systems, he will find out that with this device the movement of the centre of gravity, belonging to several objects, can be studied.
The Measuring-Seesaw can be used for both registrating a displacement of an object and for measuring forces.
To measure a little force, e.g. the force on an electrical current in the magnetic terrestrial field, at the right narrow side of the seesaw there are two small plates E and H. (Fig. 2). H is fastened at the frame of the rotatable glass disk and E opposite it at the solid frame.


Fig. 2 Fig. 3
A lever is laid on these two plates , so that its centre of gravity lies between E and H. If there is a force F1 on the right end of the lever, there is a greater force F2 = (a/b)·F1 on the plate H. The lever works as a force-amplifier. To depress the oscillation of the lever, there is a metal-plate in a bowl S, filled with oil. To bring H into line with E, there is a weight G(200g) on the seesaw, which can be moved on the glass.
In fig. 3 a narrow frame (50 cm· 8.5 cm) with 15 windings of wire can be seen. Instead of the lever it lies on E and H in south-north-direction. If a current of 5 A flows through the wire, the magnetic force of the magnetic terrestrial field can be measured with a fault<5%.
2. The seesaw in the lessons
2.1 Centre of gravity and centre of gravity-sentence
Imagine a teacher, who demonstrates the uniform movement with a glass-ball rolling over the horizontal seesaw. If a pupil sees another glass-ball lying next to the seesaw, he will propose the examination of the collision of two balls. If such a collision is carried out, the pupils are astonished, that a linear diagramm appears. In view of these facts they are helpless but very interested in an interpretation. Now they can learn how to come to an interpretation by variation of the experiments. At first the teacher should roll two balls with the same mass side by side over the seesaw. The pupils recognize in this case that the PC registrates the common distance of the balls to one end of the seesaw. If the teacher then rolls the two balls in constant distance over the seesaw behind each other, some pupils will recognize that the PC indicates the place between the two balls. If there are three or more equally heavy balls in the experiment, the PC indicates the place, whose coordinates are average-values of the coordinates belonging to the balls. If this is recognized, the Centre of Gravity can be defined:
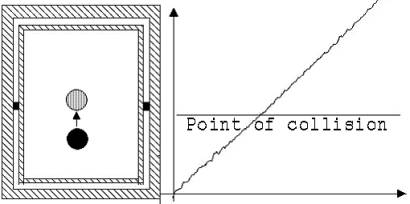
Fig. 4
We imagine a system, devided in parts of the same mass. From the coordinates of the single parts average values are formed. The point, whose coordiantes xs, ys, zs are equal to this average-values is called Centre of Gravity.
The generally known formula : xs = (x1 · m1 + x2· m2 + x3·m3 ......) / (m1 + m2 + m3....), ys = …, zs = …. can be derived now. Looking to the linear diagram drawn to the collision one can say the theorem of Centre-of -Gravity:
In a completed system the Centre of Gravity is either at rest or it moves uniformly.
For the velocity of the Centre of Gravity it can be written: vs = (v1 · m1 + v2· m2 + v3·m3 ......) / (m1 + m2 + m3....) . From the constancy of vs during the collision it can be concluded: v1·m1 + v2· m2 + v3·m3 ... = constant (theorem of momentum)..
Very impressive experiments to the theorem of Centre-of-Gravity are shown in the Figures 5 and 6.
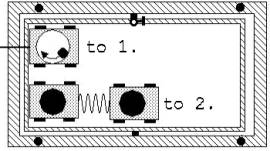
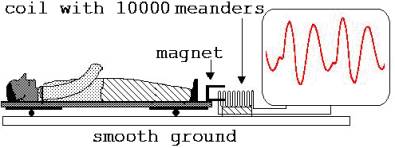
Fig. 5 Fig. 6
Fig.5:
1. A crystallizing bowl stands on a little wagon. A ball lying in the bowl is pushed into a rotation, while the wagon is held at a thread.. Then the wagon is released. It moves jerkily over the seesaw. Despite this irregular movement the PC traces a staight line diagram.
2. Two wagons are coupled with a coil spring. If the one is pushed, the two wagons change constantly their speed. The second rests while the first drives, the first rests while the second drives etc..Nevertheless a linear diagram appears.
Fig.6:
A pupil lies on a board which is kept on rolls. If blood is pumped out from a ventricle, the body moves itself to preserve the Centre-of Gravity contrary to the flow direction of the blood. The PC ist drawing a ballistocardiogram. To registrate the moving a magnet is fastened to the one end of the board, the one pole is surrounded by a coil with 10000 windings next to the board (integral of the voltage !) .
2.2 Definition of the force and the measure of force
What is a force ?
Stretching of an expander or raising a great weight are mentioned as examples. If a coil-spring ist expanded or a weight is raised, in every case there are two forces against each other. Therefore these events cannot be related to force, but to work. To avoid misunderstandings these unsuitable ideas should be replaced by better examples..
E.g. it is correct to use the word force, if a paper ball is blown away. Such and similar examples lead to the following definition:
If an object changes its velocity, after it is made mobile, one says, a force has an effect on it.
To find a useable measure of force, a movement under a definite force should be studied . Such a movement ist shown in Fig. 7.
A little wagon on the seesaw is accelerated by the stream of air coming from a hair-dryer. The hair-dryer is led behind.
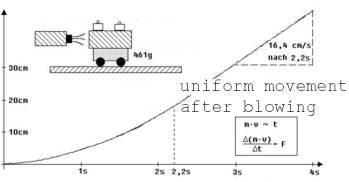
Fig. 7
2.2 seconds after the beginning of the movement, the hair-dryer is turned aside. The movement gets uniform, the continuation of the diagram gets linear. The momentary velocity at the time of 2.2 s can be determined at the linear part of the diagram.
Δ(m · v) of the air per second is constant under the described conditions . With respect to the Theorem of momentum one can say, Δ(m · v) of the wagon per second is constant too.
Therefore Δ(m · v) of the wagon is proportional to the time Δt of blowing. The quotient Δ(m·v)/Δt ( the one-second momentum). only changes, if the cause of the force (the wind) is changed. With respect to these facts Δ (m · v)/Δt is to be seen as a suitable measure of the force. The wagon (fig.7) is accelerated by the force F = Δ(m·v)/Δt = 0,034 kg·m/s².
A premise for the definition of this measure is the theorem of momentum. Every object represents a system of many atoms. If the theorem of momentum was invalid, impulse fluctuations at such an object would be possible without outer influences. In this case, it erroneously is called a force.
2.3 Introduction experiment to the topics "Centripetal Acceleration" and "Harmonic Vibration"

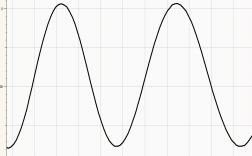
Fig. 8
A 60 g- ball rotates in a bowl standing on the seesaw.
2.4 The laws of the Throw
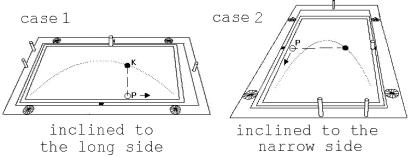
Fig. 9
The movement of a rolling ball on the seesaw inclined to the side is similar to the movement of a flying ball. The laws of the throw can be found.
2.5 Demonstration of the principle of Archimedes

Fig. 10
A tray filled with water stands on the seesaw. A little ship is pulled with a thread slowly through the water. No weight shift is measured.
2.6 Superposition of oscillations
|
Fig. 11
|
Two coil-springs oscillate at the front of the seesaw. |
|
Abb. 12 |
Demonstration of a beat |
2.7 Measuring the Centripetal Force

Fig. 13