Experimentelle Einführung in die Fehlertheorie mit dem CASSY - E
von Gerhard Höhne
Mit dem CASSE - E in Verbindung mit dem Programm MAuS (Messen, Auswerten, Simulieren) kann leicht nachgewiesen werden, daß die Gaußsche Glockenkurve die Verteilung von Meßwerten beschreibt.
Dieser Nachweis ist zum Einstieg in die Fehlertheorie sehr zu empfehlen. Die unerwartete Gesetzmäßigkeit weckt das Interesse der Schüler und auf die wichtigsten Tatsachen der Fehlertheorie kann man nach Kenntnis der Verteilungsfunktion schon nach wenigen Stunden eingehen.
1. Die Verteilung von Spannungsspitzen eines akustischen Signals
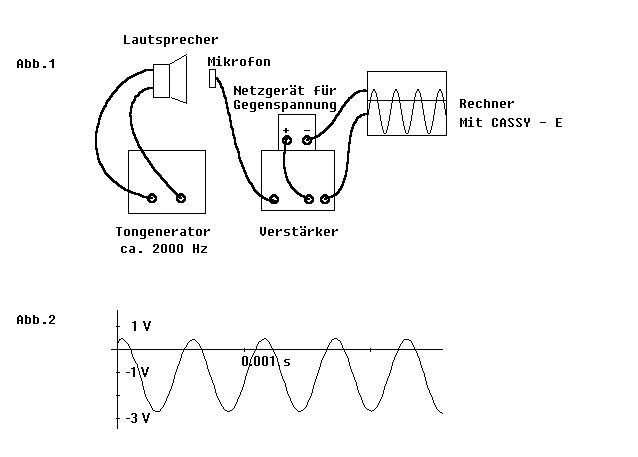
Ein 2000 Hz - Ton wird mit einem Mikrofon aufgenommen. Das verstärkte Mikrofonsignal wird mit Hilfe des CASSY - E registriert (Abb.1). Durch eine gegen das Meßsignal wirkende konstante Gegenspannung erreicht man, daß die positiven Halbwellen nicht über 0,3 V hinausgehen (siehe Abb.2 ). Deshalb können die Höhen der Spannungsspitzen in den empfindlichen Meßbereichen ± 0,3 Volt und ±1V gemessen werden, in denen die Schwankungen des Meßsignals gut erkennbar sind. Mit dem Unterprogramm „Impulse" im Meßprogramm „ MAuS " werden je Sekunde 2000 Spannungsspitzen ausgemessen. Der Meßbereich ist in 256 gleich große Intervalle aufgeteilt. Über jedem Intervall wird eine Strecke errichtet, deren Länge proportional zur Zahl der zugehörenden Meßwerte ist.
In den Abb. 3 und 4 sind Ergebnisse dargestellt, die im Meßbereich ±1V aufgenommen wurden. Deutlich ist zu sehen, wie sich die Diagramme mit zunehmender Anzahl von Messungen mehr und mehr einer Glockenkurve anpasse
.
Abb. 3
Abb. 4
2. Mathematische Untersuchung eines Verteilungsdiagramms
Eine mathematische Untersuchung soll nun an dem Diagramm in Abb. 5 durchgeführt werden. Diese Verteilungskurve zu 1000000 Messungen wurde in dem Meßbereich ±0,3 V aufgenommen.
Abb. 5
In Abb. 6 ist dieses Diagramm zusammen mit dem Graphen einer Exponentialfunktion (Glockenkurve) zu sehen, der mit dem Programm „MAuS" angepaßt wurde. Die Übereinstimmung mit dem mathematischen Graphen ist hervorragend.
Abb. 6
Der neben dem quadratischen Term (x-0,126)2 stehende Faktor ist für die Breite der Glockenkurve maßgebend. Er könnte als Maß für die Abweichungen vom Mittelwert genommen werden. Da diese Größe aber nicht veranschaulicht werden kann, sollte man einen anderen die Glockenkurve kennzeichnenden Wert suchen, welcher diesen Nachteil nicht hat. In Frage kommt der Wert m, der Abstand eines Wendepunkts von der Symmetrieachse der Glockenkurve. Im Fall (x- 0,126) = m nimmt der Exponent den Wert - 0,5 an.
Folgender Einwand erscheint gerechtfertigt:
Nur selten kann anhand der vorhandenen Meßwerte eine passende Exponentialfunktion bestimmt werden, denn es müssen hierzu sehr viele Meßwerte vorliegen. Es ist jedoch denkbar, daß man für eine geringe Zahl von Meßwerten ein Maß definieren kann, welches mit wachsender Zahl der Meßwerte gegen m strebt. Deshalb wird der Mittelwert aus den quadratischen Abweichungen (x-M)2 auf seine Eignung hin geprüft. Da m eine Länge ist, kommt nur die unter dem Namen σ bekannte Wurzel aus diesem Mittelwert in Frage. Der Rechner bestimmt σ zu jedem Verteilungsdiagramm. Für die 1000000 Meßwerte, deren Verteilung in Abb. 5 zu sehen ist, erhält man σ = 0,041. Das unter dem Namen „Mittlerer Fehler" oder „Standardabweichung" bekannte σ stimmt im Rahmen der Meßgenauigkeit mit m überein und ist somit als Streuungsmaß geeignet.
Mit welcher Wahrscheinlichkeit liegt ein Meßwert in dem Intervall [M - σ | M + σ ] ?
Diese Frage kann leicht mit Hilfe von „MAuS" beantwortet werden ?
Die gesuchte Wahrscheinlichkeit gleicht dem Verhältnis A(gepunktet)/A(gesamt) ( siehe Abb. 7).
A(gesamt): Flächeninhalt der gesamten Fläche unter der Glockenkurve .
A(gepunktet): Flächeninhalt der gepunkteten Fläche
A(gepunktet) und A(gesamt) werden durch graphische Integration mit dem Programm „MAuS" ermittelt. Für die gesuchte Wahrscheinlichkeit erhält man den Wert 0,67. 67% (genauer 68%) der Meßwerte haben von M einen Abstand ≤ σ.
Zu einem Meßwert w kann nun gesagt werden, daß der Mittelwert M sehr vieler Meßwerte (eventuell auch der wahre Wert ) mit der Wahrscheinlichkeit 68% im Bereich [w - σ| w +σ ] liegt.
Abb. 7
3. Verteilungskurve zu Zeitmeßwerten
Man könnte nun die Meinung vertreten, daß die an einem akustischen Signal gewonnenen Gesetze nicht ohne weiteres für andere Meßwerte verallgemeinert werden dürfen. Deshalb wird nun auf eine völlig andere Meßreihe eingegangen, bei der die auftretenden Schwankungen nicht am Meßsignal, sondern an der messenden Person liegen.
Abb. 8
Klickt man in den Programmen „ MAuS" unter „ Simulation" den Menüpunkt „Rotierender Zeiger zur Untersuchung einer Schwingung " an, dann erscheint ein rotierender Zeiger, der an seinem Ende ein Koordinatensystem führt. Bei einem Mausklick während der Rotation wird der Zeitunterschied zum letzten Mausklick in das Tabellenfenster II eingetragen. Der Eintragung beginnt mit dem zweiten Mausklick.
Drückt man nach jedem Umlauf auf die linke Maustaste, dann entsteht eine Tabellenspalte mit Umlaufzeiten. 2000 derartige Werte, die um den eingestellte Umlaufzeit 2 s verteilt sind - sie können von mehreren Schülern im Computerraum einer Schule schnell zusammengestellt werden - , bilden die Grundlage für die nun folgende Untersuchung mit Hilfe des in „ MAuS " integrierten Unterprogramms „ Tabellenkalkulation ".
Das Intervall [2s - 0,2 s| 2 s + 0,2 s] wird in Intervalle der Größe 0,025 s aufgeteilt. Über jedem Intervall wird eine Strecke errichtet, deren Länge proportional zur Zahl der zugehörenden Meßwerte ist. Auf diese Weise erhält man das Diagramm in Abb. 9.
Abb. 9
An den 2000 Meßwerten wird die Standardabweichung σ = 0,0343 s ermittelt. Der Graph (Glockenkurve ) zu der Funktion f(x) = 650*exp(-a *(x-2σ)2) mit a = 1/(2*σ2) [ a* σ2 = ½ ] ist ebenfalls in der Abb. 9 z u sehen. Es ist deutlich erkennbar, daß die für das akustische Signal geltenden Gesetze auch hier zutreffen. Für einen Meßwert t gilt demnach: Der wahre Wert liegt mit der Wahrscheinlichkeit 68% im Intervall [t - σ| t+σ].
Veröffentlichung in MNU 52/4 (1.6.1999 ) Seite 216 - 219