4. Lösungen zu den Aufgaben

Kapitel 1.3.4:

Zu 1.:

Der Schwerpunkt des Wagens ist in der Wagenmitte zu sehen. Zu Anfang liegt der gemeinsame Schwerpunkt von Person und Wagen rechts von der Mitte mit dem Abstand d.

d = (m_P·d_P + m_W · 0 ) / (m_W+ m_P) = 90 kg · 2,5 m / 190 kg = 1,18 m.

Die Person hat anfangs den Abstand d_P = 2,5 m von der Mitte.

Am Ende liegt der Schwerpunkt 1,18 m links von der Mitte. Da der Schwerpunkt ruht, bewegt sich der Wagen um 2·d = 2,36 m .

Zu 2.:

Der Wagen hat vor dem Ereignis in Richtung der Schiene den Impuls m₀· v₀ . Die fallenden Säcke mit je m = 50 kg haben in Schienenrichtung den Impuls 0. Somit gilt: Der Impuls des Wagens vor dem Ereignis ist gleich dem Impuls des Wagens nach dem Ereignis.

m₀ · v₀ = (m₀ + 2·m)· v   →     v = m₀· v₀/ (m₀ + 2·m)

v = 250 kg · 5m/s / (250 kg + 2·50 kg) = 3,57 m/s

Zu 3.:

Man denke sich ein Koordinatensystem, dessen x-Achse nach rechts weist. Unter dieser Voraussetzung ist v₁ = - 2 m/s und v₂ >0.

m₁· v₁+ m₂ · v₂ = 0     →     v₂ = - (m₁ / m₂) · v₁ , v₂ = 300 / 250 m/s = 1,2 m/s

Kapitel 1.3.7 :

Zu 1.:

Der Geschwindigkeitszuwachs während der Beschleunigungszeit Δt beträgt Δv =  a·Δt.

v = v₀ + Δv = v₀ + a · Δt;   a = F/m

v = v₀ + F/m · Δt     →     v = 0,5 m/s + 0,3N / 0,2 kg · 4s = 6,5 m/s

_Zu 2.:

Sofort nach dem Zusammenstoß ist der Impuls (m_B + m_W)·v des Gebildes Bremsklotz + Wagen gleich dem Impuls des Wagens vor dem Stoß. (m_B + m_W)·v = m_W · v₀. Nach dem Stoß wird der Bremsklotz mit dem Wagen unter der Kraft F = 0,5 N auf die Geschwindigkeit 0 abgebremst. Die Geschwindigkeitsänderung Δv während des Bremsens ist demnach gleich v.

v = a·Δt; a = F/(m_B + m_W )     →     Δt = v ·(m_B + m_W ) / F

v = m_W · v₀ / (m_B + m_W )     →     Δt = m_W · v₀ / F     →     Δt = 0,3 kg · 3m/s / 0,5 N = 1,8 s

Kapitel 1.4.1

Zu1.:

(m₁ +m₂) · a = m₂ · g   →   a = m₂ · g /(m₁ +m₂)

v = a · t = [m₂ · g /(m₁ +m₂)] · t ;   s = (1/2)· a · t² = ½· [m₂ · g /(m₁ +m₂)] · t²

v = 0,02 kg ·9,81 m/s² · 3 s / 0,22 kg = 2,67 m/s

s = ½ · 0,02 kg ·9,81 m/s² · 9s² / 0,22 kg = 4,01 m

Zu2.:

Der Gegenstand erreicht in der Zeit t seinen höchsten Punkt mit der Koordinaten y (am Koordinatenursprung beginnt der Wurf) und hat dann die Geschwindigkeit 0. Die Geschwindigkeitsänderung in t ist somit v₀ .

v₀ / t = g ; t = v₀ / g = 10m/s / 9,81m/s² = 1,02 s

y = - ½ · g ·t² + v₀ ·t = 5,1 m

Wurfdauer: t_W = 2·t = 2,04 s

Zu 3.:

Am Ort des Aufschlags sei der Ursprung eines Koordinatensystems, dessen y-Achse nach oben weist.

y = - ½ ·g · t² + v₀ · t + y₀ ; beim Aufschlag gilt: y = 0

- ½ · g · t² + v₀ · t + y₀ = 0     →     - ½ · 9,81m/s² · t² – 5 m/s · t + 10m = 0

Es handelt sich um eine quadratische Gleichung mit den Lösungen: t₁ = - 2s (unpassend) und t₂ = 1s

v = -g·t + v₀ ;     v = - 9,81 m/s² · 1 s – 5 m/s ;     v = - 14,81 m/s

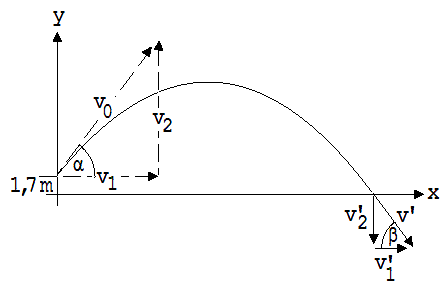
Zu 4.:

v₁ = v₀ · cos α ;     v₂ = v₀ · sin α

Wurfhöhe:

Am höchsten Punkt ist v_y = 0 ( t ist die Steigzeit)

v_y = v₂ - g · t     →     t = v₂ / g

y = - ½ ·g · t² + v₂ · t + y₀ ( y₀ = 1,7 m )

y = - ½ ·g · v₂² / g² + v₂² / g + y₀

y = ½ · v₂² / g +y₀

y = ½ · v₀² · sin²(α) / g + y₀     →     y = 7,4 m

Wurfweite : y = - ½ · g · t² + v₂ · t + y₀ ( t steht nun für die Wurfzeit ).

Beim Aufschlag gilt : y = 0

0 = - ½ · g · t² + t· v₀ · sin α + y₀ (quadratische Gleichung für t )

t₁ = - 0,15 s (unpassend) ;     t₂ = 2,3 s

Wurfweite x = v₁ · t₂ = v₀ · (cos α ) · t₂     →     x = 24,4 m

Geschwindigkeit des Aufschlags:

Vektor v der Endgeschwindigkeit: v = v₀ + a· t = {v₀ · cos(α) ; v₀ · sin(α) - g· t₂ }   ={ v’₁ ; v’₂ } = { 10,6 m/s; -12 m/s }   →   Geschwindigkeit |v| = 16 m/s

Aufschlagwinkel: tan(β)= 12 / 10,6     →     β = 48, 5°

Kapitel 1.4.2

Zu 1.:

Der Boden des Eimers und die Erde üben Kräfte auf das Wasser aus. Am höchsten Punkt ist die Summe aus der Bodenkraft F_B und der Gewichtskraft m · g die Zentripetalkraft auf das Wasser der Masse m.

m ·g + F_B = m ·v² /r

Ist F_B = 0, dann hält sich das Wasser gerade noch im Eimer.

m·g = m ·v² /r     →     g = v² /r     →     v² = g·r   →     v = 2,8 m/s

Zu 2.:

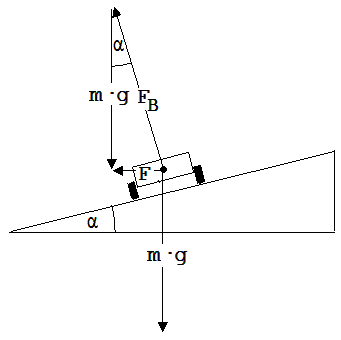
Die Straße und die Erde üben die Kräfte F_B und m·g auf das Auto aus. Die Zentripetalkraft F ist die Resultierende aus diesen beiden Kräften.

tan α = F / (m · g );   F = m ·v² /r

↓

tan α = v² /(g · r)   →   α = 57°

Zu 3.:

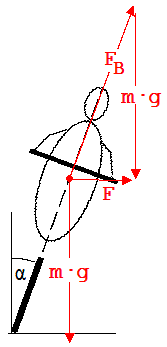
Die Straße und die Erde üben auf den Fahrer und das Fahrrad (gemeinsamer Schwerpunkt !) die Kräfte F_B und m·g aus .

m = Masse des Fahrrads + Masse des Fahrers

tan α = F / (m · g); F = m ·v² /r

↓

tan α = v² / (r · g)   →     α = 8,9 °

Zu 4. :

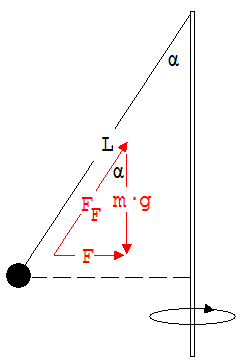
Der Faden und die Erde wirken mit den Kräften F_F und m·g auf die Kugel ein. Die Resultierende dieser beiden Kräfte wirkt als Zentripetalkraft F.

tan α = F/(m · g); F = m · ω² · r     →     tan α = ω² · r/ g

r = L · sin α; sin α / cos α = ω² · r/ g

↓

sin α / cos α = ω² · L · sin α /g     →     1/cos α = ω² · L /g

↓

cos α = g /(ω² · L )     →     α = 78°

Zu 5.:

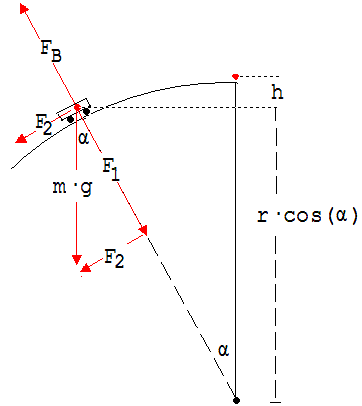
Die Gewichtskraft kann man in die zwei Komponenten F₁ und F₂ zerlegen. F₂ sorgt für die Beschleunigung entlang der Bahn. F₁ bildet mit F_B die Zentripetalkraft. F_B ist die Kraft, welche das Rohr auf das Wägelchen ausübt. An der Ablösestelle ist F_B = 0.

In diesem Fall gilt:

F₁ = m · v² /r ; F₁ = m · g · cos α

↓

m·g·cos α = m·v² /r     →     cos α = v² /(r · g)

v² ist durch die Höhenänderung

h = r - r · cos α = r·( 1 – cos α ) bestimmt.

Es gilt : v² = 2 ·g · h = 2 ·g · r · ( 1 – cos α )

cos α = v² /(r · g)

↓

cos α = 2 ·g · r · ( 1 – cos α ) / (r · g )

cos α = 2 · ( 1 – cos α )     →     cos α = 2/3     →     α = 48°

Kapitel 1.5.2

Zu 1.:

G wird von der Erde mit m₁ ·g nach unten gezogen. Dieser Kraft wirkt der Faden mit der Zugkraft F entgegen. Die resultierende Kraft ist m₁ · g – F.

a · m₁ = m₁ · g – F

Der 160 g – Körper wird vom Faden mit F nach oben gezogen. Der Kraft F wirkt die Erde mit m₂ ·g entgegen.

a· m₂ = F – m₂ ·g     →     F = a ·m₂ + g · m₂

Setzt man den letzten Term in die erste Gleichung ein, dann erhält man:

a·m₁ = m₁ ·g – a · m₂ – g ·m₂     →     a = (m₁· g – m₂ · g ) / (m₁ + m₂ )

a = 40g · 9,81 m/s² /360 g = 1,09 m/s²; v = a·t = 1,09 m/s² · 0,5 s = 54 cm

s = (a/2) · t² = 13, 6 cm

Zugkraft F des Fadens :

F = a ·m₂ + g · m₂     →     m₂ · ( a + g ) = 0,16 kg · 10,9 m/s² = 1,74 N

Kraft auf die Rolle = 2·F = 3,48 N

Diese Kraft ist kleiner als die Gewichtskraft der am Faden hängenden Gegenstände !

Zu 2.:

Auf W₂ wirkt die schiefe Ebene mit F_N (Normalkraft) und die Erde mit m· g. Die Resultierende aus diesen beiden Kräften ist die Hangabtriebskraft F_H.

F_H = m₂ ·g · sin(40°) ; F_H beschleunigt die beiden Wagen

a = m₂ ·g · sin(40°) / (m₁ + m₂ ) = 0,15 kg · 9,81 m/s² /0,35 kg = 2,7 m/s²

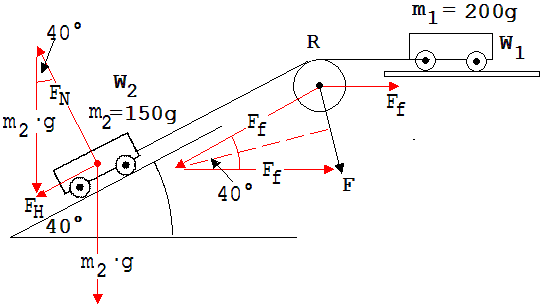
Von zwei Seiten zieht der Faden an der Rolle mit der Kraft F_f. Die beiden von links und rechts wirkenden Kräfte bilden F als Resultierende.

F_f = m₁· a

F = 2·F_f · sin(20°)

F = 2 · m₁ · a · sin(20°) = 0,36 N

Zu 3.:

Das linke Gewicht wird unter der Kraft m · g - F_f beschleunigt. F_f = Zugkraft des Fadens nach oben.

m · g – F_f = m · a₁ (a₁ = Betrag der Beschleunigung) → F_f = m · g - m · a₁

Das rechte Gewicht wird unter 2 · F_f - m · g nach oben beschleunigt.

2·F_f - m · g = m · a₂; a₂ = a₁ /2     →     2 · F_f - m · g = m · a₁ /2     →     F_f = m·g /2 + m · a₁/4

F_f = m · g - m · a₁ ;   F_f = m · g /2 + m · a₁ /4     →     m · g - m · a₁ = m · g /2 + m · a₁ /4 a₁ = (2/5) · g

Zu 4.:

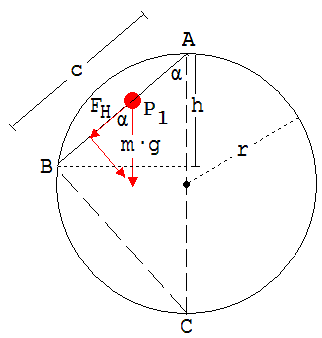
Für die Endgeschwindigkeit v der Perle am Punkt B gilt: v² = 2·g·h. Die Gleitzeit t erhält man nach v = t · a

t = v / a ( a ist die Beschleunigung der Perle).

t² = v²/a² = 2· g · h / a²

F_H = m·a; m · g / F_H = g / a = c / h → a = g ·h / c

t² = 2 · c² / (g · h)

Das Dreieck A,B,C ist nach dem Thalessatz rechtwinklig, somit gilt: h · (2r) = c² (Kathetensatz ! )

↓

t² = 4 · r/g

t² ist unabhängig vom Verlauf der Sehne immer gleich 4 · r/g.

Kapitel 1.6.3.1:

Zu 1.: Das Auto wird unter der Gleitreibungskraft F_R = F_N · µ gebremst.

F_N = m · g     →     F_R = m · g · µ

m · g · µ = m · a ( a = |a| )     →     a = g · µ

Da a der Bewegung entgegen gerichtet ist , schreiben wir a = - g · µ.

Für die Bremszeit t gilt demgemäß: v₀ / t = g · µ     →     t = v₀ /(g · µ)

Für den Bremsweg s gilt:   s = - a/2 · t² + v₀ ·t ( a ist der Bewegung entgegen gerichtet)

↓

s = (- g· µ/2) · v₀² / (g·µ)² + v₀² / (g·µ)   →   s = 0,5 · v₀² / (g·µ)

↓

s = 0,5 ·(100· 1000/3600 m/s)² / (9,81 m/s² ·0.8 ) = 49,15 m

Der Bremsweg ist dem Quadrat der Geschwindigkeit proportional !

Bei 150 km/h ist der Bremsweg 1,5² · 98,3 m = 221 m.

Es ist noch anzumerken, dass auch beim Anfahren die Beschleunigung nicht über g·µ_H hinausgehen kann. Wird die Lauffläche der Räder stärker beschleunigt, dann drehen die Reifen durch.

Zu 2.:

Sofort nach dem Stoß ist der Impuls, den der Wagen zusammen mit dem Bremsklotz hat, gleich dem Impuls des Wagens vor dem Stoß.

(m₂ + m₁ ) · v₀ = m₁ · v ; v₀ = Geschwindigkeit sofort nach dem Stoß.

Anschließend werden beide Gegenstände mit F = m₂ · g · µ abgebremst.

(m₂ + m₁ )· a = m₂ · g · µ (a = |a| )   →     a = g · [µ ·m₂ / (m₂ + m₁ )]

s = - a/2 · t² + v₀ ·t ( die Beschleunigung ist der Bewegung entgegen gerichtet) ;

t = v₀ /a     →     s = ½ · v₀² / a

↓

s = ½ · v₀² · (m₂ + m₁ )/ (g · µ ·m₂) → s = 25 cm

Zu 3.:

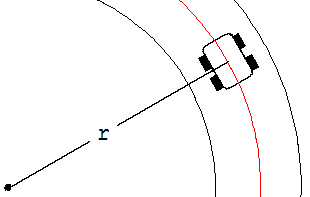
Die Zentripetalkraft geht von der Straße aus. Sie beträgt höchstens µ ·m ·g.

µ·m·g = m ·v² /r → µ ·g = v² / r

↓

v² = µ·g· r = 21 m/s = 75,6 km/h

Hinweis:

In der Aufgabenstellung wird man zunächst eine Angabe über die Masse m vermissen. Wenn eine Zahlenangabe zu fehlen scheint, dann sollte man eine Variable für sie setzten in der Hoffnung, dass diese bei der Behandlung der Aufgabe durch Kürzen herausfällt.

Kapitel 1.8:

Zu 1.:

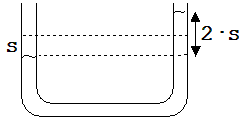
Es gilt T = 2 · π · √(m/D). D und m müssen berechnet werden.

Bläst man in einen Schenkel hinein und bewirkt damit die Auslenkung s, dann stellt sich im anderen Schenkel ein um 2·s höherer Wasserspiegel ein.

Die Gewichtskraft auf die Wassersäule der Länge 2·s ist die zurück treibende Kraft F.

F = 2·s ·A · ρ · g ( ρ = Dichte des Wassers, A = Querschnitt des Rohrs )

↓

D = F / s → D = 2 ·A · ρ · g; m = L · A · ρ

↓

T = 2· π · √[L / (2·g)]; ν = 1/(2· π) · √(2·g / L)

T = 0,77 s; ν = 1,28 Hz

Zu 2.:

Während einer ¼ - Schwingung wird beschleunigt. t = T/4 = π/2 · √(m / D) ≈ 5 ms

Zu 3.:

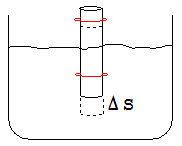
Es gilt T = 2·π · √(m/D). D und m müssen berechnet werden. Wird der Stab aus seiner Ruhestellung um Δs nach unten gedrückt, dann erfährt er eine um F = Δs · A · ρ ·g höhere Auftriebskraft (A = Querschnitt des Stabes, ρ = Dichte des Wassers). F wirkt als zurück treibende Kraft.

D = F / Δs = A · ρ ·g; m = A · L · ρ_H     →     T = 2· π · √[L· ρ_H / (g · ρ)] = 0,69 s

Zu 4.:

Der Haftvorgang ist eine Halbschwingung. Mit steigender Stoßgeschwindigkeit nimmt die Verformung s der Kugeln beim Stoß zu. F/s bleibt nicht konstant, sein mittlerer Wert wird größer. Da die Schwingungszeit mit steigendem D abnimmt, werden die Kontakte kürzer, wenn der Anfangsabstand vergrößert wird.

Zu 5.:

Es gilt: T = 2·π· √(L/g)   →     g = 4·π²· L /T² ; T = 138,8 s / 40 = 3,47 s     →     g = 9,83 m/s²

Zu 6.:

Die Erdanziehungskraft m ·g wird um die Auftriebskraft vermindert, welche die Kugel vom Wasser erfährt. In T = 2·π· √(L/g) ist für g ein kleinerer Wert einzusetzen. In vertikaler Richtung wirkt auf die Pendelkugel die Kraft F = m · g - V·ρ·g .

V = Volumen der Eisenkugel, ρ = Dichte des Wassers , ρ_E = Dichte des Eisens

V · ρ_E = m → V = m / ρ_E     →   F = m · g · (1 - ρ/ ρ_E )

In T = 2·π· √(L/g) muss für g der Wert g · (1 – ρ/ ρ_E ) eingesetzt werden.

T = 2·π· √{L/[g · (1 – ρ/ ρ_E )] }   →   T = 1,176 s

Kapitel 1.11.2:

Zu 1.:

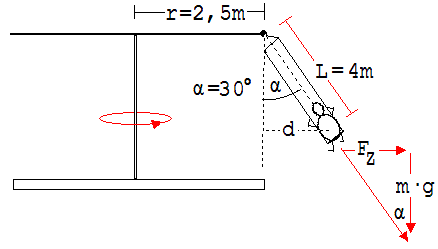
Das Kind mit der Masse m hat von der Drehachse den Abstand r + d.

d = L ·sin(α)

Bei der Winkelgeschwindigkeit ω erfährt es die Zentrifugalkraft F_Z.

F_Z = m · ω² · [ r + L ·sin(α)]

Die Resultierende aus F_Z und der auf das Kind wirkenden Gewichtskraft m · g ist parallel zu L.

m · ω² · [ r + L ·sin(α)] / (m ·g) = tan(α)     →     ω = 1,12 s^-1

Zu 2.:

Wir betrachten eine kleine Wassermenge M der Masse m auf der Wasseroberfläche. Auf M wirkt die Gewichtskraft m ·g und die Zentrifugalkraft m·ω²·x ( x = r ! ). Da M nicht entlang der Oberfläche verschoben wird, muss die Resultierende aus den beiden Kräften senkrecht zur Wasseroberfläche stehen. Die Parabeltangente durch M hat den Steigungswinkel α. tan(α) ist die Steigung y' = dy/dx = 2·k·x.

y' = m·ω²·x / (m ·g) = ω²·x / g   →     k = ½ · ω² / g → y = ½ ·ω² ·x²/g

Zu 3.:

Die linke und die rechte Feder haben die Federkonstanten D. Die zurück treibende Kraft bei einer Schwingung auf einer ruhenden Scheibe beträgt demnach F = 2·D·x. Unter ihr schwingt die Kugel auf einer ruhenden Scheibe mit der Frequenz f_R.

f_R = 1/(2·π) · √(2·D/m)     →     D = 4·π² · f_R² · m / 2     →     D = 1,97 N/m

Auf der rotierenden Scheibe wirkt der Federkraft die Zentrifugalkraft m·ω²· x entgegen.

Die zurücktreibende Kraft ist somit F = 2·D·x - m·ω²· x = (2·D - m·ω²)· x

(2·D - m·ω²) = D’     →     D’ = 3,54 N/m

↓

f = 1/(2·π) · √(D’/m)     →     f = 0,94 Hz