2.1 Das Relativitätsprinzip

In einem gleichförmig fahrenden Eisenbahnwagen fällt ein Körper so wie in einem ruhenden Raum nach Galileis Fallgesetz. Es sieht danach aus, dass eine solche Gleichartigkeit für jedes Experiment gilt und deshalb mit keinem Experiment in einem geschlossenen Raum entschieden werden kann, ob dieser Raum in Ruhe oder in gleichförmiger Bewegung ist.

Relativitätsprinzip: In gleichförmig zueinander bewegten Systemen gelten gleiche Gesetze.

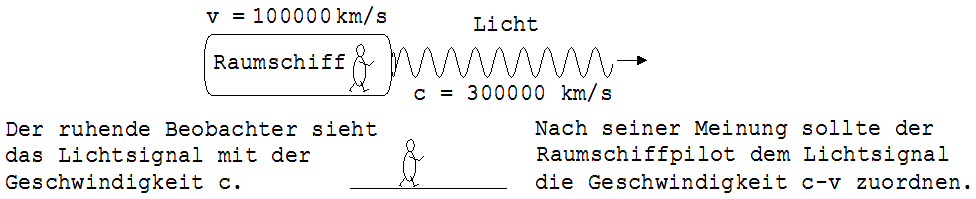
Bei Gedankenexperimenten mit Lichtsignalen hat man den Eindruck, dass dies Relativitätsprinzip zu Widersprüchen führt. In Abb. 2.1.1 ist ein mit v = 100000 km/s fliegendes Raumschiff zu sehen, von dem ein Lichtsignal ausgesandt wird. Dieses Signal hat aus der Sicht eines ruhenden Beobachters A die Geschwindigkeit c = 300000 km/s, denn die Lichtgeschwindigkeit wird nicht von der Geschwindigkeit der Lichtquelle beeinflusst. Nach dem Relativitätsprinzip ordnet ein Passagier B des Raumschiffs dem Lichtsignal auch die Geschwindigkeit c’ = 300000 km/s zu. A kann die Behauptung c = c’ zunächst nicht anerkennen, da aus seiner Sicht das Raumschiff dem Lichtsignal mit 100000 km/s folgt. In Bezug auf das Raumschiff sollte das Lichtsignal seiner Meinung nach die Geschwindigkeit 200000 km/s haben. Die Behauptung c’ = 200000 km/s ist jedoch mit dem Relativitätsprinzip unvereinbar.

Abb. 2.1.1

A hat möglicherweise nur scheinbar Recht. Er geht davon aus, dass sich die Messmittel von B so verhalten wie die eigenen. Es ist jedoch nicht auszuschließen, dass mit bewegten Messmitteln (Uhren, Messlatten....) andere Messergebnisse erhalten werden als mit ruhenden. So ist denkbar, dass die Längen-, Massen-, und Zeiteinheiten infolge schneller Bewegung aus der Sicht von A größer oder kleiner werden. Die folgende, scheinbar in sich widersprüchliche Behauptung könnte demnach doch zutreffen:

Obwohl die Relativgeschwindigkeit des Lichtes in Bezug auf das Raumschiff aus der Sicht von A 200000 km/s beträgt, misst B die nach dem Relativitätsprinzip zu erwartende Lichtgeschwindigkeit c' = 300000 km/s.

Im nächsten Kapiteln wird gezeigt, dass Anwendungen des Relativitätsprinzips auf Gedankenexperimente innerhalb eines schnell fliegenden Raumschiffs zu richtigen Schlussfolgerungen führen, was als Bestätigung des Relativitätsprinzips gelten kann. Es stellt sich die experimentell beweisbare Tatsache heraus, dass die Masse eines Teilchens bei Geschwindigkeiten nahe der Lichtgeschwindigkeit größer ist als seine Ruhemasse.

2.2 Die Änderung der Masse infolge Bewegung

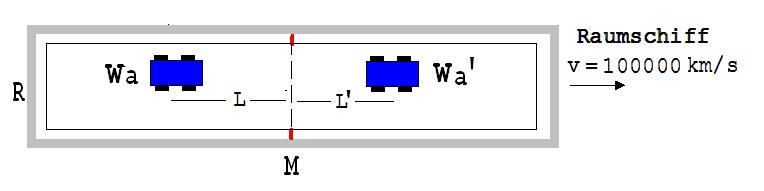
Abb. 2.2.1

In einem mit der Geschwindigkeit v = 100000 km/s fliegendem Raumschiff ( siehe Abb. 2.2.1) steht eine sich sehr weit nach links und rechts erstreckende Experimentierwippe. Ein Passagier B beschleunigt von der in der Mitte der Wippe liegenden Drehachse M aus zwei gleiche Experimentierwagen Wa und Wa’ völlig gleichartig nach links und rechts ( in und entgegen der Flugrichtung ). Nach dem Relativitätsprinzip sind die aus seiner Sicht gleichförmig dahingleitenden Wagen Wa und Wa´ zu jeder Zeit von M gleich weit entfernt.

Sind die beiden Abstände L und L’ von M auch aus der Sicht von A gleich, wenn das Relativitätsprinzip als gültig vorausgesetzt wird ?

Zunächst erscheint L = L’ selbstverständlich.

Zweifel hieran stellen sich ein, wenn man an zwei Lichtsignale denkt, die von M aus gleichzeitig den beiden Wagen nachschickt werden. Nach dem Relativitätsprinzip müssten die Signale die Wagen gleichzeitig erreichen, denn aus der Sicht von B entfernen sich die beiden Signale nach links und rechts mit gleicher Geschwindigkeit. Für A hat M von dem linken Signal einen größeren Abstand als vom rechten. Somit müsste aus seiner Sicht L’<L sein. Wenn dies zutrifft, dann muss der Beobachter A dem Wagen Wa’ eine größere Masse zuordnen als dem Wagen Wa, denn die Wippe erfährt keine Drehung, wenn B sie am Rahmen R anhebt und dabei darauf achtet, dass beide Wagen die gleiche Beschleunigung a erfahren. Unter Berücksichtigung des Hebelgesetzes schließt A daraus, dass die Masse von Wa' größer ist als die von Wa.

a·m · L = a·m’· L’    →     m / m’ = L’ / L = k < 1    →    m < m’

Zur Berechnung von L’ / L = k setzen wir voraus, dass sich Wa aus der Sicht von B genauso schnell von M entfernt wie die Erde. Wa ist dann in Bezug auf die Erde in Ruhe. A vergleicht demgemäß einen ruhenden Wagen Wa mit einem Wagen Wa', der mit der Geschwindigkeit u nach rechts gleitet. Der Experimentator B in der Rakete prüft die Entfernungen von Wa und Wa’, indem er gleichzeitig nach links und rechts Lichtsignale aussendet. Kehren diese Signale nach Reflexion an den Wagen gleichzeitig bei ihm zurück, haben somit gleiche Laufzeiten, dann sieht er die Abstände der Wagen von M als gleich an.

Es wird nun gezeigt, dass nach dem Relativitätsprinzip unter diesen Bedingungen aus der Sicht des irdischen Beobachters L’ < L zutrifft und dass sich daraus die experimentell nachprüfbare Schlussfolgerung m’ > m ergibt.

Der Ausgangspunkt für die Untersuchung mit dem Ergebnis L’ < L ist folgende Überlegung:

Die Laufzeiten der beiden Lichtsignale T_links und t_rechts stimmen auch aus der Sicht von A überein. Es ist denkbar, dass diese Zeiten T_links und t_rechts mit Hilfe von L und L’ bestimmbar sind. In diesem Fall könnte man die für T_links und t_rechts gültigen Terme einander gleich setzten und hätte somit eine Gleichung, die den Vergleich von L und L’ zulässt.

Für das auf Wa’ gerichtete Lichtsignal gilt:

Hinweg: c · t₁ = L’+ u · t₁ → t₁ = L’/(c-u)

c: Lichtgeschwindigkeit

u: Geschwindigkeit von Wa’ in Bezug auf A

L’: Abstand des Wagens Wa’ von M beim Start des Lichtsignals !!

t₁: Zeit für den Hinweg

Während der Zeit t₁ wird der Weg des Lichtes zu Wa’ um u · t₁ verlängert; somit ist der Hinweg des Lichtsignals nicht gleich L’, sondern gleich L’+u · t₁ .

Rückweg: c · t₂= L’ + u · t₁ - v · (t₁ + t₂)

t₂: Rücklaufzeit des Lichtsignals, v: Geschwindigkeit des Raumschiffs

Während des Hin- und Rücklaufs kommt M dem Lichtsignal um v·(t₁+t₂) nach, somit erhält man den Rückweg, indem man den Hinweg L’+ u ·t₁ um v·(t₁ +t₂) verkürzt.

Aus den Gleichungen für Hin- und Rückweg folgt:

c · t₁ + c · t₂ = 2 · (L’+ u · t₁) - v · (t₁ + t₂)

c · (t₁ + t₂) + v · (t₁ + t₂) = 2 · (L’+ u · t₁) → t₁ + t₂ = (L’ + u · t₁) · 2 / (c + v)

Im rechten Teil der Gleichung wird für t₁ der Term L’ /(c-u) eingesetzt.

t₁ + t₂ = [L’ + u · L’ /(c-u)] · 2 / (c + v) = [ (c ·L’- u·L’+ L’·u) /(c-u)] · 2 / (c + v)

t₁ + t₂ = L’ · c/(c-u) · 2/ (c + v)

Laufzeit t = t₁ + t₂ = L’ ·c · 2/ [(c + v) · (c - u)]

Für das nach links auf Wa gerichtete Signal gilt:

L: Abstand des Wagens Wa von M beim Start des Lichtsignals !!

Hinweg: c · T₁ = L

Rückweg: c · T₂ = L + v · (T₁+T₂); T₁: Hinlaufzeit ; T₂: Rücklaufzeit

Während des Hin- und Rücklaufs entfernt sich M von Wa zusätzlich um v·(T₁+T₂)

Aus den beiden Gleichungen für den Hin- und Rückweg folgt:

c · (T₁ + T₂) = 2·L + v · (T₁+T₂) → c · (T₁ + T₂) - v · (T₁+T₂) = 2·L

Laufzeit T = T₁+ T₂ = 2 · L / (c-v)

Wegen T₁ + T₂ = t₁ + t₂ gilt: 2·L/(c - v) = 2 · L’· c / [(c - u)·(c + v)]

L’ / L = k = (c-u) · (c + v) / [c · (c-v)]

Für L’/L schreiben wir k. Es wird eine Gleichung gewünscht, welche die Abhängigkeit des Verhältnisses k = L’/L von der Geschwindigkeit u der Kugel Wa’ zeigt. Deshalb muss die Raumschiffgeschwindigkeit v durch einen von u abhängigen Term ersetzt werden.

Es gilt:

(L + L’)/L = u / v     →     1 + L’ / L = u / v    →     v = u/ ( 1+ L’/L)    →    v = u / (1+k)

Anmerkung: L + L’ (Abstand zwischen Wa und Wa’) und L sind die Wege, welche Wa’ und M aus der Sicht des irdischen Beobachters nach dem Anstoß vor dem Aussenden des Lichtsignals zurückgelegt haben. L’+ L und L verhalten sich wie die entsprechenden Geschwindigkeiten u und v zueinander. Unter Berücksichtigung von v = u / (1+ k) kann nun geschrieben werden:

k = [(c-u) · (c+ u /(1+k)] / [c · (c-u / (1+k)]

Es wird mit (1+k) erweitert.

k = [(c-u) · (c + c · k + u)] / [c · (c + c · k - u)]

Beide Seiten werden mit [c · (c + c · k - u )] multipliziert.

k · c² + k² ·c² - k · c· u = c² + c² · k + c· u - u · c - u · c · k - u²

↓

c² · k² = c² - u² → k² = 1 – u²/c²

↓

L'/L  =  √(1- u² / c² )

Wa und Wa' sind aus der Sicht von B immer gleich weit von M entfernt. Dementsprechend dreht sich die Wippe auch nicht in ihrem Rahmen R, wenn B diesen Rahmen packt und nach oben beschleunigt, denn die von M gleich weit entfernten Wagen üben aus der Sicht von B hierbei links und rechts von M gleiche Kräfte auf die Wippe aus. Für den ruhenden Beobachter sind Wa und Wa' nicht gleich weit von M entfernt. Da auch er keine Drehung wahrnehmen kann, folgert er anhand des Hebelgesetzes L'· m' = L·m     →     L’/L = m/m’    →     m/mʼ = √(1- u² / c² ) .

↓

mʼ = m / √(1- u² / c² )

m ist die Masse des aus der Sicht von A ruhenden Wagens Wa. Diese Masse wird auch dem Wagen Wa’ in Ruhe zugeordnet, denn die beiden Wagen sind einander gleich.

Schlussfolgerung: Für die Masse m eines Körpers gilt: m= Ruhemasse/√(1- u² / c² ) . Für die Ruhemasse (u = 0) schreiben wir von nun an m_{0 .}

Mit m = m₀ / √(1- u² / c² wird die Bahn schneller Elektronen richtig berechnet. Dadurch erfährt das Ergebnis des hier durchgeführten Gedankenexperiments eine Bestätigung.

Das nachfolgende Diagramm ( Abb. 2.2.2 ) zeigt an, wie sich die Masse eines Körpers (m₀ = 1kg) mit zunehmender Geschwindigkeit ändert. Erst bei Geschwindigkeiten in der Größenordnung der Lichtgeschwindigkeit sind deutliche Abweichungen von der Ruhemasse zu erkennen.

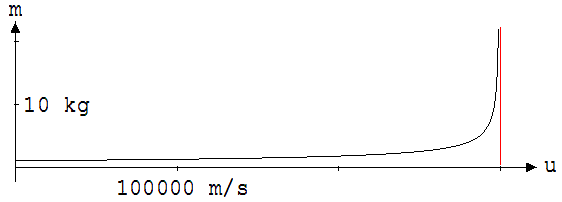
Abb. 2.2.2

2.3 Masse und Energie

Die Masse eines Körpers nimmt mit seiner kinetischen Energie zu. Anhand des im Kapitel 2.2 beschriebenen Gedankenexperiments (Abb. 2.2.1 ) kann leicht eine Beziehung zwischen dem Massenzuwachs und der kinetischen Energie hergeleitet werden .

Wenn der aus der Sicht von A ruhende Wagen W der Masse m auf das hintere Ende der Wippe stößt, dann wird er aus der Sicht von B elastisch reflektiert. A sieht diesen Vorgang als eine Beschleunigung aus der Ruhe auf die Geschwindigkeit u und ordnet ihm eine Beschleunigungsarbeit W in der Zeit Δt mit der Kraft F zu. Während der Beschleunigung des Wagenschwerpunkts am hinteren Ende der Wippe (der Wagen W wird etwas gestaucht) wird W unter der Kraft F um v · Δt verschoben.

F = [(m₀/k) ·u] /Δt ; k² = 1 – u²/c²

(m₀/k) ·u beschreibt die Impulsänderung in der Zeit Δt (Anfangsimpuls = 0, m₀ = Ruhemasse, m₀/k = m). Für die gegen den Wagen verrichtete Arbeit W gilt demnach:

W = F ·v ·Δt → W = [(m₀ ·u / k) /Δt ]·v · Δt → W = m₀ ·u ·v / k

Unter Berücksichtigung der in Kapitel 2.2 hergeleiteten Gleichung v = u / (1 + k) erhält man für W:

W = m₀·u² /[k·(1+k)]

Die Erweiterung des Bruchterms mit (1-k) führt zu:

W = m₀·u²·(1-k)/ [k·(1- k²)] ; k² = 1 – u²/c² → W = m₀·u²·(1-k) / (k·u²/c²)

↓

W = (m₀/k – m₀)·c²

m₀/k: Wagenmasse nach der Beschleunigung, m₀: Ruhemasse des Wagens

m₀/k – m₀ = m – m₀ : Massenzuwachs Δm

↓

W = Δm · c²

Die Energie des Wagens Wa nimmt um ΔE = W zu. Es wird noch bewiesen, dass die Beziehung zwischen Masse- und Energieänderung ΔE=Δm·c² nicht nur für kinetische- , sondern für jede Energieart gültig ist. So kann man mit ihr z.B. die Energie berechnen, die bei der Spaltung oder der Verschmelzung von Atomkernen frei wird. Voraussetzung für eine solche Rechnung ist die Kenntnis der Gesamtmassen von Ausgangs- und Endprodukten.

Da die Masse eines Körpers unendlich groß wird, wenn seine Geschwindigkeit der Lichtgeschwindigkeit zustrebt, kann er niemals auf Lichtgeschwindigkeit beschleunigt werden, da hierzu eine unendlich hohe Energie erforderlich wäre.

Die Lichtgeschwindigkeit ist eine Grenzgeschwindigkeit.

Mit E_kin = m₀· u²/ 2 wurde bisher die kinetische Energie eines Körpers der Masse m₀ mit der Geschwindigkeit u berechnet. Nach obiger Rechnung gilt: Δm · c² = W = m₀·u² /[k·(1+k)]. Wenn u erheblich kleiner als c ist, dann kann mit k ≈ 1 geschrieben werden: Δm · c² ≈ m₀·u²/2.

2.4 Die Zeitdilatation (Zeitdehnung)

Die Gleichungen über die Massenänderung sind experimentell bestätigt worden. Das Relativitätsprinzip kann somit als richtig gelten.

Es wurde darauf hingewiesen, dass dieses Prinzip nur dann der Wirklichkeit entsprechen kann, wenn sich Längenmaße und Uhren bei Bewegung anders verhalten als in Ruhe. In diesem Zusammenhang muss deutlich gemacht werden, dass die Feststellung, ein System sei in Ruhe, willkürlicher Natur ist. Wird ein System als Ruhesystem definiert, dann nennen wir ein davon abweichendes System bewegt.

Es soll nun der Frage nachgegangen werden: Wie ändern sich Längenmaße und Uhren , wenn sie von einem ruhenden- in ein bewegtes System gebracht werden?

Wir stellen uns während des schon mehrfach beschriebenen Gedankenexperiments (Abb. 2.2.1 ) zwei mit den Wagen Wa und Wa’ fliegende Uhren U und U’ vor , die zu Beginn des Experiments auf die Zeit 0 gestellt wurden.

Beide Uhren erreichen aus der Sicht des Raumschifffahrers B gleichzeitig das linke- und rechte Ende der Wippe und zeigen hierbei auch gleiche Zeiten t an. Der ruhende Beobachter A sieht dies anders. Wenn sich die ruhende Uhr U am linken Ende der Wippe im Abstand L von M befindet und die Zeit t anzeigt, dann ist Uʼ erst Lʼ = L·√(1- u²/c²) < L von M entfernt und hat deshalb noch nicht das rechte Wippenende erreicht. U’ gelangt später als die ruhende Uhr U zum Ende der Wippe und zeigt deshalb die Zeit t später an. Bewegte Uhren gehen für A demnach langsamer als ruhende Uhren.

Welches t’ sieht A auf der Uhr U’, wenn die Uhr U am linken Ende des Raumschiffs die Zeit t anzeigt ?

A stellt nach den Zeitangaben von U’ fest: Wenn die ruhenden U die Zeit t anzeigt, dann kann man auf der im Abstand L' von M befindlichen Uhr U' die Zeit t' ablesen. Uʼ zeigt die Zeit t erst im Abstand L von M an.

t’/t = L’ / L; L’ / L = √(1- u²/c²)    →    t’ = t ·√(1- u²/c²)    →    t = t’ /√(1- u²/c²)

Diese Gleichung lässt einen wichtigen Schluss zu:

Wenn auf einer ruhende Uhr die Zeit t abgelesen wird, dann zeigt eine bewegte Uhr, die gleichzeitig mit der ruhenden Uhr auf 0 gestellt wurde, eine kleinere Zeit t' an. Bewegte Uhren gehen langsamer.

Nach dem Relativitätsprinzip hat ein bestimmter Vorgang in einem ruhenden Laboratorium die gleiche Dauer wie in einem bewegten Laboratorium, wenn die Zeit seines Ablaufs jeweils mit der Uhr des Laboratoriums gemessen wird.

In einem Laboratorium werde t₀ als Dauer eines Vorgangs gemessen. Ein Beobachter, der das Laboratorium mit der Geschwindigkeit u sieht, ordnet mit seinen Uhren diesem Vorgang die Zeit t = t₀/√(1- u²/c²) zu. Aus seiner Sicht wird das Ereignis infolge der Bewegung zeitlich gedehnt (Zeitdilatation).

2.5 Längenkontraktion

Wir stellen uns vor, die beiden Wagen Wa und Wa’ der Abb.2.2.1 würden aus der Sicht des im Raumschiff arbeitenden Experimentators zwei gleich lange Messlatten direkt hinter sich herziehen. Die Messlatte an Wa ruht für den irdischen Beobachter. Der Messlatte an Wa’ ordnet er die Geschwindigkeit u zu.

Die Enden dieser Messlatten erreichen gleichzeitig die Mitte M der Wippe. Aus der Sicht eines ruhenden Beobachters sind sie nicht gleich lang, sondern gleichen den Abständen L und Lʼ zwischen den Wagen und M.

Lʼ = L·√(1- u²/ c² )

Wir sehen: Einem bewegten Gegenstand wird in Bewegungsrichtung eine geringere Länge zugeordnet als in Ruhe (Längenkontraktion). Dies gilt nicht für einen Stab, der mit der Geschwindigkeit u quer zur Bewegungsrichtung fliegt. Ihm werden von dem ruhenden- und mitbewegten Beobachter gleiche Längen zugeordnet.

Beweis:

Wie in Abb.2.5.1 angedeutet, misst der mitbewegte Beobachter B die Länge L’ des Stabes [EF] in folgender Weise. Er schickt von E ein Lichtsignal nach F. Bei F wird dieses Signal von einem Spiegel reflektiert und kehrt wieder zu E zurück. B gibt als Streckenlänge L’ den Wert c·t’ an. t’ ist die halbe Laufzeit des Lichtsignals.

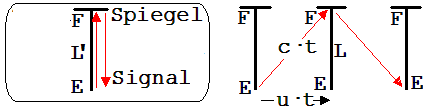
Abb. 2.5.1                                   Abb. 2.5.2

Aus der Sicht des ruhenden Beobachters A bewegt sich das Lichtsignal auf der in Abb. 2.5.2 dargestellten Bahn. Während das Lichtsignal von E nach F und wieder zurück gelangt, bewegt sich der Stab [EF] mit der Geschwindigkeit u nach rechts. A berechnet die Länge L von [EF] nach dem Lehrsatz des Pythagoras:

c² ·t² - u² ·t² = L²    →    L = c ·t ·√( 1 – u²/c² )

t ist die vom ruhenden Beobachter gemessene halbe Laufzeit des Lichtes.

Wegen t = tʼ / √( 1 – u²/c² ) gilt: L = c ·tʼ = Lʼ

2.6 Über die Einstellung von Uhren, die an verschiedenen Orten aufgestellt sind (Synchronisation)

Mehrere an verschiedenen Orten aufgestellte Uhren sollen nach einer Uhr Q eingestellt werden. Es erscheint zunächst empfehlenswert nach folgender Anweisung vorzugehen: Man nehme die Uhr Q, fahre mit ihr zu den verschiedenen Orten und stelle jeweils die dort vorhandenen Uhren nach Q ein.

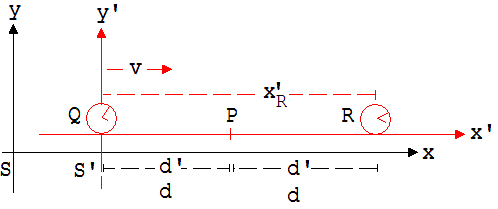
Abb. 2.6.1

Überdenkt man dieses Verfahren, dann erweist es sich als mangelhaft, da der Gang der Uhr Q von der Reisegeschwindigkeit abhängt. Besser ist folgende Methode: Zur Einstellung einer Uhr R in einem Systems S nach einer anderen am Koordinatennullpunkt von S liegenden Uhr Q wird ein Ort P in S gesucht, der genau zwischen R und Q liegt. Von diesem Ort werden Lichtblitze ausgesandt. Hierbei wird die Uhr R so eingestellt, dass ein von P kommendes Lichtsignal bei R und Q gleichzeitig eintrifft. Werden die Uhren eines zur Erde mit der Geschwindigkeit v bewegten Systems S' in gleicher Weise synchronisiert, dann wird man erfahren, dass Ereignisse, die aus der Sicht eines mitbewegten Beobachters gleichzeitig stattfinden, für einen irdischen Beobachter nicht immer gleichzeitig sind. Dieser Sachverhalt soll hier eingehend anhand der Abb. 2.6.1 untersucht werden. S sei ein in Bezug auf die Erde ruhendes, S’ ein mit der Geschwindigkeit v zur Erde bewegtes Koordinatensystem. Die beiden mitbewegten Uhren Q und R seien so eingestellt, dass ein von P ausgehendes Lichtsignal Q und R in gleicher Zeigerstellung zum Zeitpunkt t' antrifft.

d: Abstände P-Q und P-R in Bezug auf einen irdischen Beobachter A.

xʼ_R ; d’: Abstände in Bezug auf einen mitbewegten Beobachter B.

Von A aus gesehen benötigt das Lichtsignal zu der Uhr Q die Zeit t₁ und zu der Uhr R die Zeit t₂.

t₁ · c = d – v· t₁ → t₁ = d/(c + v), t₂ · c = d + v· t₂ → t₂ = d/(c-v)

Demzufolge erreicht es R um ∆t = t₂ – t₁ später als Q. Aus der Sicht des irdischen Beobachters geht infolgedessen die Uhr Q gegenüber der Uhr R vor. Wenn das Lichtsignal die Uhr Q erreicht, dann zeigt diese die Zeit t' an. Anschließend läuft Q aus der Sicht von A bis zum Eintreffen des Lichtsignals bei R um ∆t’ = ∆t· k, k = √(1 - v²/c²) weiter. Das heißt, wenn bei R die Zeit t' abgelesen wird, dann zeigt Q die Zeit t'+∆t’ an.

∆t = t₂ - t₁ = d /(c-v) – d /(c + v) = 2 ·d ·v / (c² - v²) = 2 ·d ·v / (c² ·k²)

Unter Berücksichtigung der Zeitdilatation Δt = Δt’/k und der Längenkontraktion x’_R ·k = 2 ·d finden wir:

Δt’/k = x’_R ·k · v /(c² ·k²) → Δt’ = x’_R·v/c²

2.7 Die Lorentztransformationen

Ein Flugkörper bewege sich mit der Geschwindigkeit v zur Erde. S’ ist das zu diesem Flugkörper, S das zur Erde gehörende Koordinatensystem (siehe Abb. 2.7.1). Der Flugkörper sei mit Uhren und Längeneinheiten ausgerüstet, die auch auf der Erde üblich sind. Die an den verschiedenen Stellen des Flugkörpers aufgestellten Uhren seien entsprechend den auf der Erde gültigen Vereinbarungen aufeinander abgestimmt (synchronisiert).

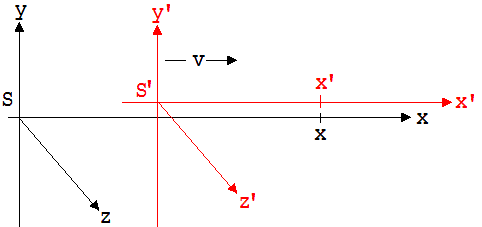
Abb. 2.7.1

Als Zeitnullpunkt gelte in beiden Systemen der Augenblick, in dem die beiden y-Achsen zusammentreffen. An einem Punkt P werde von einem mitbewegten und einem irdischen Beobachter ein Ereignis wahrgenommen, t ist die hierzu gehörende irdische Zeit, x ist der von einem irdischen Beobachter A gemessene Abszissenwert des Ereignispunktes, t’ und x’ sind die entsprechenden Werte des mitbewegten Beobachters B.

Wie können die zu einem System gehörenden Werte errechnet werden, wenn die Werte des anderen Systems bekannt sind ?

x – v · t ist der von einem irdischen Beobachter gemessene Abstand des Punktes P zu dem Koordinatenursprung des bewegten Systems. (x – v ·t) beschreibt eine durch Längenkontraktion verkleinerte Strecke mit der Ruhelänge xʼ.

xʼ · k = (x – v ·t)    →    1.) x’ = (x – v ·t)/k;   k= √( 1 – v²/c² )

Zum Zeitpunkt t liest der irdische Beobachter auf der bewegten Uhr am Ursprung von S’ die Zeit tʼ₀ ab. Unter Berücksichtigung der Zeitdilatation erhält man:

t’₀ = t · k (Die bewegte Uhr geht langsamer !)

Die Zeit t’, die er zum gleichen irdischen Zeitpunkt t auf der mitbewegten Uhr am Ort P abliest, weicht von t’₀ um x’ ·v/c² ab.

t’₀ – t’ = x’ ·v/c² ; t’₀ = t · k    →    t·k = t’ + x’ ·v/c²    →    2.) t = (t’ + x’ ·v/c²)/k

Die Gleichungen l und 2 ermöglichen auch die Berechnung von x bei Kenntnis von x’ und t’ und die von t’ bei Kenntnis von x und t. Im ersten Fall muss die Zeit t in der 1.Gleichung durch den in der 2. Gleichung für t stehenden Term ersetzt und die hiermit gewonnene Gleichung nach x aufgelöst werden. Im zweiten Fall ist x’ der 2. Gleichung gegen den rechten Term der 1. Gleichung auszutauschen. Hiernach ist nach t’ aufzulösen. Die insgesamt gewonnenen Beziehungen, Lorentztransformationen genannt, sind in der folgenden Tabelle 1 zusammengefasst.

Da die quer zur Bewegungsrichtung liegenden Strecken keine Längenkontraktionen erfahren gilt für die y – und z-Koordinaten eines abseits von der x-Achse liegenden Punktes: y = y’ und z = z’ .

Es ist nun zu prüfen, ob die Lorentztransformationen mit dem Relativitätsprinzip im Einklang sind.

Die Transformationsgleichungen sind nur dann annehmbar, wenn mit ihnen die folgenden Schlussfolgerungen aus dem Relativitätsprinzip begründet werden können:

1. Die Lorentztransformationen gelten auch dann, wenn man S’ als ruhend und S als bewegt ansieht.

2. Wenn ein Beobachter in S die Uhren in S’ langsamer laufen sieht als eine Uhr in S, dann müssen für einen Beobachter in S’ die Uhren in S langsamer gehen als die in S’.

3.Wenn der Beobachter in S einem in S’ liegenden 1m-Maßstab eine Länge < 1m zuordnet, dann muss ein Beobachter in S’ einen in S liegenden 1m-Maßstab ebenfalls verkürzt sehen.

4. Wenn sich eine Lichtwelle in S nach allen Seiten mit der Geschwindigkeit c ausbreitet, dann gilt dies auch in S’.

Zu 1.: Nach Umkehrung der x-Achsen ( S wird als bewegtes System gesehen) sollten die unter 2. angegebenen Transformationsformeln gelten:

v’ ist die Geschwindigkeit von S aus der Sicht von S’.

Beweis:

Wenn man die Achsen der Koordinatensysteme umkehrt, dann müssen in den Gleichungen unter 1. die Vorzeichen von x und x’ umgekehrt werden. Nach Umkehrung der Vorzeichen erhält man die unter 3. angegebenen 4 Transformationsgleichungen, die mit den Gleichungen unter 2. übereinstimmen, wenn die Geschwindigkeit v’ von S aus der Sicht von S' gleich v ist.

v = v’ ist noch zu beweisen !

Für das in S’ dem Koordinatenursprung von S zugeordnete x’ gilt:

x = (x’ – v ·t’)/k = 0    →    x’ – v ·t’ = 0 → x’ = v ·t’    →    v’ = x’/t’ = v

Zu 2.

In S sei eine Uhr U an einem Ort P mit der Koordinate x aufgestellt (siehe Abb. 2.7.2). Wenn diese Uhr die Zeit t₁ anzeigt, steht der Zeiger einer ihr augenblicklich benachbarten Uhr U’₁ in S’ auf t’₁. In der Folgezeit entfernt sich U’₁ von P, andere Uhren des Flugkörpers erreichen U.

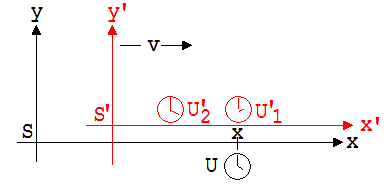
Abb. 2.7.2

Wenn U die Zeit t₂ anzeigt, dann gibt die ihr dann benachbarte Uhr U’₂ die Zeit t’₂ an. Der mit der Uhr U gemessenen Zeit t₂ – t₁ ordnet der Beobachter B in S’ die Zeit t’₂ – t’₁ zu. Es gilt:

t’₁ = (t₁ – v ·x/c²)/k, t’₂ = (t₂ – v · x/c²)/k

t’₂ - t’₁ = (t₂ – t₁ )/k    →    t’₂ – t’₁ > t₂ – t₁

Aus t’₂ - t’₁ > t₂ – t₁ folgert B: Die Uhren in S laufen langsamer als die in S’.

Aus der Sicht des ruhenden Beobachters A ist t’₂ zu groß, weil für ihn die Uhr U’₂ gegenüber der Uhr U’₁ vorgeht. Demgemäß fällt seiner Meinung nach die Zeitdifferenz t’₂ – t’₁ zu groß aus.

Es erscheint zunächst unsinnig, dass je nach Standpunkt des Beobachters die Uhren des Flugkörpers schneller oder langsamer laufen als die der Erde. Es muss hierbei bedacht werden, dass ein irdischer Beobachter beim Vergleich bewegter und ruhender Uhren jeweils eine bewegte Uhr mit zwei an verschiedenen Orten der Erde aufgestellten Uhren vergleicht. Im Gegensatz dazu vergleichen Beobachter des bewegten Systems eine irdische Uhr mit zwei bewegten Uhren, die aus der Sicht des irdischen Beobachters verschiedene Zeiten angeben.

Zu 3.

[x₁ x₂] sei eine Strecke auf der x-Achse eines ruhenden Koordinatensystems. Beobachter in einem System S’, welches sich in Achsenrichtung bewegt, messen die zu x₁ und x₂ gehörenden x’ -Werte nach ihren Uhren gleichzeitig zum Zeitpunkt t’ und ordnen der Strecke [x₁ x₂] die Länge x’₂ – x’₁ zu .

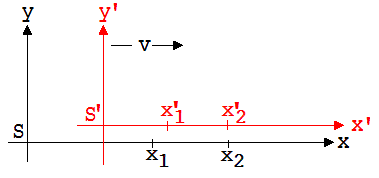
Abb. 2.7.3

Aus der Sicht eines irdischen Beobachters wird xʼ₂ nach xʼ₁ gemessen. Da in der Zwischenzeit der Punkt in S’ mit x’₁ nach rechts rückt, fällt aus seiner Sicht xʼ₂ und damit auch die Differenz x’₂ – x’₁ zu klein aus.

Nach den Lorentztransformationen gilt: x₁ = (x’₁ + v ·t’)/k ;    x₂ = (x’₂ + v ·t’)/k

↓

x₂ – x₁ = (x’₂ – x’₁)/k    →    x’₂ - x’₁ = (x₂ – x₁) · k    →    x’₂ – x’₁ < x₂ - x₁

Es wurde früher gezeigt, dass bewegte, zur Ausbreitungsrichtung parallele Strecken dem irdischen Beobachter kleiner erscheinen als gleichartige ruhende Strecken. Da dies der gerade hergeleiteten Ungleichung zu widersprechen scheint, muss darauf hingewiesen werden, dass irdische Beobachter die Anfangs- und Endkoordinaten x₁ und x₂ einer bewegten Strecke nach irdischen Uhren gleichzeitig messen, während die bewegten Beobachter die entsprechenden Koordinaten x’₁ und x’₂ einer ruhenden Strecke nach den Uhren ihres System zum gleichen Zeitpunkt bestimmen.

Zu 4.

Zum Zeitpunkt t = t’ = 0 werde an dem zu diesem Zeitpunkt gemeinsamen Koordinatenursprung von S und S’ eine kugelförmige Welle ausgesandt. P sei ein Punkt, der zu einem Zeitpunkt (t, t’) auf der Wellenfront der Kugelwelle liegt. Für seinen Abstand L vom Koordinatenursprung des Systems S gilt:

L² = x² + y² + z² = c²· t²

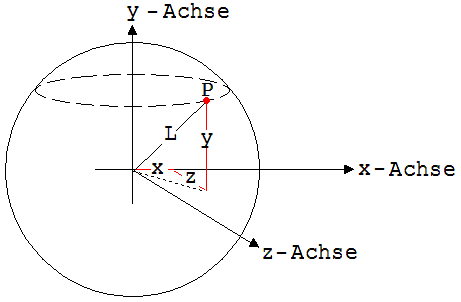
Abb. 2.7.4

Hieraus folgt unter Berücksichtigung der Lorentztransformationen:

(x’ + v ·t’)² / k² + y’² + z’² = c²· (t’ + v ·x’/c²)²/ k²

↓

x’² + v²·t’² + 2·x’·v· t’ + y’² · k² + z’² · k²   =   t’² · c² + x’² · v²/c² + 2·x’ ·v ·t’

↓

x’² - x’² · v²/c² + y’² · k² + z’² · k²   =   t’² · c² -v²·t’²

↓

x’² · (1- v²/c²) + y’² · k² + z’² · k²   =   c² · t’²· (1- v²/c²); k² =  (1- v²/c²) !

↓

x’² + y’² + z’² = c² · t’²

Hiernach entfernt sich die Welle in S’ so wie in S nach allen Seiten mit der Geschwindigkeit √(x’² + y’² + z’² ) /t’ = c vom Koordinatenursprung.

2.8 Das Additionstheorem der Geschwindigkeiten

Ein System S’ bewege sich mit der Geschwindigkeit v in Bezug auf ein ruhendes System S. Ein Gegenstand P fliege mit der Geschwindigkeit u’={u'_x, u'_y} in S’. Zum Zeitpunkt t = t’ = 0 durchlaufe P den Nullpunkt beider Systeme.

Wie kann die Geschwindigkeit u ={u_x, u_y} im System S anhand von u’ bestimmt werden ?

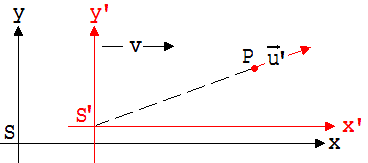
Abb. 2.8.1

1. Berechnung von u_x

u_x = x / t = [(x’ + v ·t’) / k] / [(t’ + v ·x’/ c²) / k];   k =√(1 - v² / c²)

u_x = (x’ + v · t’) / (t’ + v · x’/ c²) = (x’/ t’ + v ) / (1 + v ·(x’/ t’) / c²)

u_x = (u'_x + v) / (1 + v ·u'_x / c²)

2. Berechnung von u_y

u_y= y/t = y’/ [(t’ + v·x’ / c²) / k] = u’_y ·k / (1 + v·u'_x / c²)

Die Gleichungen zur Berechnung von u’_x und u’_y anhand von u_x und u_y werden in ähnlicher Weise hergeleitet.

Es gilt: u’_x = (u_x – v) / (1 - v ·u_x / c²);     u’_y = u_y ·k / (1 - v ·u_x / c²)

Anwendungsbeispiel: Ausbreitung von Licht in fließendem Wasser

Nach Herleitung eines Gesetzes ist ein Anwendungsbeispiel wünschenswert. Führt ein solches Beispiel zu einem nachweisbaren Ergebnis, dann hat meine einen Beleg für die Richtigkeit des Gesetzes.

Mit dem Additionsgesetz der Geschwindigkeiten kann die Geschwindigkeit berechnet werden, mit der sich Licht in fließendem Wasser in Fließrichtung ausbreitet (siehe Abb. 2.8.2).

Die Fließgeschwindigkeit des Wassers ist v. Das Licht hat in Bezug auf einen im Wasserstrom treibenden Beobachter die Geschwindigkeit c_W.

Das Verhältnis c / c_W (c = c_Vakuum) heißt Brechungsindex n des Wassers.

↓

c_W = c/n

Abb. 2.8.2

Nach dem Additionsgesetz der Geschwindigkeiten finden wir für die Lichtgeschwindigkeit im Wasser in Bezug auf einen ruhenden Beobachter:

c'_W = (c / n + v)/[1+ ( v·c / n ) / c²] = (c / n + v) / [1+ (v / c) / n]

Für die durch die Fließgeschwindigkeit v verursachte Geschwindigkeitsänderung des Lichtes erhalten wir:

Δc = c'_W – c / n = (c / n + v) / [1+ (v / c) / n] – c / n = (c / n + v – c / n – v / n²) / [1+ (v / c) / n]

Anmerkung: - c/n = {- c/n ·[1+ (v / c) / n]} / [1+ (v / c) / n]

Δc = v· (1 – 1/ n² ) / [1+ (v / c) / n]

Unter Berücksichtigung von v<<c (v gegenüber c vernachlässigbar klein) können wir auch schreiben: Δc = v· (1 – 1/n² )

Die letzte Gleichung wurde von dem französischen Physiker Fizeau im 19. Jahrhundert anhand von Messdaten aufgestellt.

2.9 Transformation der Masse und des Impulses und der Kraft

2.9.1 Transformation von Massen und Impulsen

Impulse und Massen werden wie Ortskoordinaten und Zeiten transformiert !

pʼ_y = p_y

Beweis:

In S erhalten wir die Ruhemasse m₀ nach m₀ = m · √(1 – u²/c² ) und in Sʼ nach m₀ = mʼ ·√(1– uʼ²/c² ).

Somit gilt : m · √(1 – u²/c² ) = mʼ ·√(1– uʼ²/c² )

Die Geschwindigkeitskoordinaten von u im Term 1 – u² / c² = 1 – ( u_x² + u_y² ) / c² werden nach dem Additionstheorem durch uʼ_x und uʼ_y ersetzt. Nach einer umfangreichen algebraischen Umformung findet man:

√(1 – ( u_x² + u_y^{2 )}/c² ) = √(1 – uʼ²/c² ) · √(1 – v²/c² ) / (1 - v ·uʼ_x/c²)

↓

m = (mʼ + mʼ · uʼ_x ·v /c²) /k → m = (mʼ + pʼ_x ·v /c²) /k

pʼ_x = mʼ· uʼ_x , k = √(1 – v²/ c²)

Für mʼ erhält man in ähnlicher Weise: mʼ = (m - p_x ·v /c²) /k

Aus Gleichungen für m und mʼ können die Transformationsformeln für p_x und pʼ_x hergeleitet werden.

Zum Beweis der Gleichung p_y = pʼ_y ( m·u_y = mʼ·uʼ_y ) wird m’ durch (m - p_x ·v /c²) /k und uʼ_y durch u_y ·k / (1 - v ·u_x/c²) (Additionstheorem der Geschwindigkeiten) ersetzt.

mʼ·uʼ_y = [(m - p_x ·v /c²) /k] · u_y ·k / (1 - v ·u_x/c²)

mʼ·uʼ_y = m · [(1 - u_x ·v /c²) /k] · u_y ·k / (1 - v ·u_x/c²) = m· u_y

pʼ_y = p_y

2.9.2 Transformation der Kraft

1. Kraft in x,x'-Richtung:

F_x = Δp_x / Δt = [(Δpʼ_x + v· Δmʼ )/k] /[ ( Δtʼ + Δxʼ · v / c² )/k]

F_x = (Δpʼ_x / Δtʼ + v· Δmʼ / Δtʼ ) / ( 1 + Δxʼ/ Δtʼ · v / c² ),     Δpʼ_x / Δtʼ = F'_x ,      Δxʼ / Δtʼ = u'_x

↓

F_x = ( F'_x + v· Δmʼ / Δtʼ ) / ( 1 + u'_x · v /c² )    →    F_x = {F'_x + (v / c²)· Δmʼ ·c²/Δtʼ } / (1 + u'_x · v /c² )

Δmʼ·c² ist die im xʼ ;yʼ- System gegen den Körper K verrichtete Arbeit.

Δmʼ·c² = Fʼ_x · Δxʼ + Fʼ_y · Δyʼ + Fʼ_z · Δzʼ    →     Δmʼ ·c² / Δtʼ = Fʼ_x · u'_x + Fʼ_y · u'_y + Fʼ_z · u'_z

Δyʼ / Δtʼ = u'_y ,     Δzʼ / Δtʼ = u'_z

F_x = {F'_x + (v / c²) · (Fʼ_x · u'_x + Fʼ_y · u'_y + Fʼ_z · u'_z) } / (1 + u'_x · v / c² )

F_x = {F'_x · (1+ u'_x · v / c² ) + Fʼ_y · u'_y + Fʼ_z · u'_z} / (1 + u'_x · v / c² )

F_x = F_x' + {Fʼ_y · u'_y + Fʼ_z · u'_z } / (1 + u'_x · v / c² )

Findet keine Verschiebung quer zur Bewegungsrichtung statt, dann gilt: F_x = F'_x .

2. Kraft in y,y'-Richtung:

F_y = Δp_y / Δt;    Fʼ_y = Δpʼ_y /Δtʼ

Die Impulsänderungen sind in beiden Systemen gleich groß.

F_y = Δpʼ_y / Δt, Δt = ( Δtʼ + Δxʼ · v / c² ) / k    →    F_y = Δpʼ_y / [( Δtʼ + Δxʼ · v / c² ) / k]

F_y = (Δpʼ_y / Δtʼ) / [( 1 + u'_x · v / c² ) / k]    →    F_y = F'_y / [( 1 + u'_x · v / c² )/ k]

Im Fall u'_x = 0 gilt:   F_y = Fʼ_y · k

2.10 Satz von der Erhaltung der Masse

Wir denken uns ein abgeschossenes System aus mehreren Teilchen 1, 2, ... Die x-Koordinate des i. Teilchenimpulses nennen wir p_i. Für die Summe Σp_i aus den Impulskoordinaten p_i aller Teilchen gilt:

Σp_i = (Σp’_i + v·Σm’_i) /k   →   Σm’_i = (k ·Σp_i - Σp’_i ) /v

Aus der letzten Gleichung können wir unter Berücksichtigung des Impulssatzes folgenden Schluss ziehen:

Die Gesamtmasse eines abgeschlossenen Systems bleibt konstant.

Die Gleichung E = Δm · c² ist demnach nicht nur für die kinetische Energie, sondern für jede Energieart gültig.

Wird z.B. ein fliegender Körper von einer Feder abgebremst, dann bleibt die Gesamtmasse vom fliegenden Objekt und der Feder konstant. Während die Masse des einen Gegenstandes zunimmt, nimmt die des anderen ab. Der Massenzuwachs einer Spiralfeder während einer Stauchung kann auch anhand des in der Abb. 2.10.1 dargestellten Gedankenexperiments bestimmt werden.

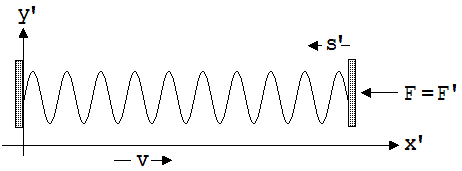
Abb. 2.10.1

In einem mit der Geschwindigkeit v gleichförmig bewegten System wird aus der Sicht eines mitbewegten Beobachters B’ in dem Zeitabschnitt Δt’ eine Spiralfeder um s’ gestaucht (siehe Abb. 2.10.1). Die dabei verrichtete Arbeit errechnet er nach F’·s’ unter der Annahme, dass s’ sehr klein ist und somit die Kraft F’ während der Verformung als konstant angesehen werden kann. F’·s’ ist die Energiezunahme ΔE’ der Feder aus der Sicht von B’. Die am linken Rand fixierte Feder erhält aus seiner Sicht im bewegten System keinen Impuls, da die auf sie von links und rechts wirkenden Kraftstöße gleich groß sind. Anders sieht dies ein ruhender Beobachter A. Für ihn sind die Wirkungszeiten Δt_L und Δt_R der links und rechts angreifenden Kräfte verschieden. Die Kräfte sind in beiden Systemen gleich groß.

Die zur Stauchung führende Kraft F wirkt aus der Sicht von A am linken Ende vom Zeitpunkt t_1L bis zum Zeitpunkt t_2L und am rechten Ende von t_1R bis t_2R. Aus der Sicht von B’ erfolgt die Stauchung zwischen den Zeitpunkten t’₁ und t’₂.

Δt_L = t_2L – t_1L ; Δt_R = t_2R – t_1R

t_1L = t’₁ /k; t_2L = t’₂ /k → Δt_L = Δt’/k

t_1R = [t’₁ + (v/c²) ·x’₁]/ k ;  t_2R = [t’₂ + (v/c²) ·x’₂]/ k

x’₁ und x’₂: x’-Werte vom rechten Ende der Feder vor und nach der Stauchung.

Δt_R = t_2R - t_1R = [(t’₂ - t’₁ ) + (v/c²) · (x’₂ - x’₁) ]/ k → Δt_R = [Δt’ – (v/c²) · s’]/ k

s’ = x’₁ – x’₂: Stauchung aus der Sicht von B’.

F = F’

Der ruhende Beobachters A registriert eine Impulsänderung Δ(m·v) an der Feder.

Δ(m·v) = F· Δt_L – F · Δt_R = F · (Δt_L – Δt_R )

F · (Δt_L – Δt_R ) = F · (v/c²) ·s’/ k

Da sich v nicht ändert gilt: Δ(m·v) = v · Δm.

v · Δm = F · (v/c²) · s’/ k   →   Δm · k = (1/c ²) · s’ ·F’

Δm · k ist die Änderung der Ruhemasse Δm’ im bewegten System.

Somit gilt: Δm’ ·c² = s’ · F’ = ΔE’

2.11 E = h·f

Herleitung der Planckschen Beziehung anhand eines Gedankenexperiments

Wir denken uns, wie in der nebenstehenden Skizze angedeutet, einen gleichförmig mit der Geschwin-digkeit v bewegten Spiegel, auf den Licht der Frequenz f fällt.

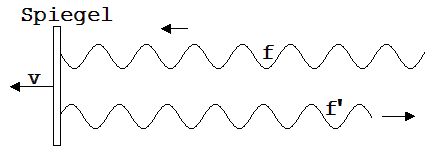
Abb. 2.11.1

Das Licht hat bekanntlich Energie und somit auch eine Masse, übt dementsprechend eine Kraft auf den bewegten Spiegel aus und verrichtet hierbei eine Arbeit, die zu einem Energieverlust des Lichtes führt. Neben der Energie nimmt auch die Frequenz ab; dies ist leicht einzusehen, wenn man bedenkt, dass durch die Bewegung des Spiegels das reflektierte Signal und somit auch die Periodenlänge gestreckt wird. Mit der größeren Wellenlänge stellt sich nach λ · f = c eine kleinere Frequenz f’ ein.

Meistens sind Energieverluste des Lichts nicht mit einer Frequenzänderung verbunden. Man denke z.B. an die Lichtschwächung durch einen Graufilter oder durch Wolken.

Warum wird im einen Fall der Energieverlust von einer Frequenzänderung begleitet, im anderen Fall aber nicht ?

Zur Beantwortung dieser Frage sollte man sich nach ähnlichen Phänomenen umschauen.

Man stelle sich ein Gas in einem senkrechten Zylinder unter einem beweglichen Kolben vor, der mit Gewichten belastet ist. Werden die Gewichte entfernt, dann dehnt sich das Gas aus, wobei seine Temperatur und seine Energie infolge der von ihm verrichteten Arbeit abnimmt. Hier ist anstelle der Frequenz die Temperatur eine energieabhängige Größe. Man kann die Energie des Gases aber auch dadurch verringern, indem man einen Teil des Gases aus seinem Behälter ausströmen lässt.

Während im ersten Fall die Zahl der Gasatome konstant bleibt und die Energie der einzelnen Atome abnimmt, verhält es sich im zweiten Fall genau umgekehrt. Die Zahl der Atome wird kleiner, die Energie der einzelnen Atome bleibt konstant.

Unter dem Eindruck der erwähnten Tatsachen erscheint nun eine Deutung des zu Anfang vorgestellten Gedankenexperiments leicht möglich.

Die Lichtenergie ist in Wirkungseinheiten (Photonen, Quanten) eingeteilt. Der bewegte Spiegel vermindert die Energie der einzelnen Photonen, ein Filter schluckt Photonen, und vermindert damit die Energie eines Lichtstrahls. Die Frequenz des Lichtes ist von der Energie der Photonen abhängig.

Welche Beziehung besteht zwischen der Frequenz und der Photonenenergie ?

Die Frequenz- und Energieänderung während der Lichtreflexion werden nun berechnet.

1. Änderung der Frequenz

Ein Wellenzug der Länge n ·λ wird in der Reflexionszeit t auf die Länge n ·λ’ gestreckt. Während der Reflexion legt das Ende des ankommenden Wellenzuges die Strecke n ·λ + v·t zurück.

n ·λ + v · t = c · t   →   t = n ·λ /(c-v)

Der Anfang des reflektierten Wellenzuges entfernt sich in dieser Zeit vom Spiegel um: c · t + v · t = t·(c + v) = n·λ’

t·(c + v) = n·λ’; t = n ·λ /(c-v)   →   (c + v)·n·λ /(c-v) = n·λ’

↓

(1.) λ/λ’ = f’/f = (c-v)/(c+v)

2. Änderung der Energie

Der Spiegel erfährt in der Reflexionszeit t die Kraft F = [ m · c - (-m’ · c)] / t = c·(m + m’) / t. m und m’ sind die Lichtmassen vor und nach der Reflexion. [ m·c - (-m’ · c)] ist die Impulsänderung während der Reflexion.

Für die Lichtarbeit gilt: W = F · v · t = [c · (m + m’) / t] · v · t = v · c · (m + m’)

v · t beschreibt die Verschiebung des Spiegels in der Zeit t.

Für die Arbeit des Lichtes gilt auch: W = (m – m’) ·c²

Somit können wir schreiben: v · c · (m + m’) = (m – m’) ·c²

v · (m + m ’) = c·(m - m’)   →   m’ · (c + v) = m · (c – v)

(2.) m’/m = (c-v)/(c+v)

(1.) f’/f = (c-v)/(c+v); (2.) m’/m = (c-v)/(c+v)   →   f’ / f = m’ /m

Die Massen m und m’ verhalten sich zueinander wie die zugehörenden Energien E und E’.

m’ / m = E’/E; f’ / f = m’ / m   →   E’/f’ = E/f

Für die Energien E_P und E_P’ der Photonen gilt dann auch: E’_P/f’ = E_P/f = Konstante

Diese Konstante heißt Wirkungsquantum h.

E_P = h · f

Mit diesem Gesetz kann der Fotoeffekt erklärt werden. Dieser Effekt ermöglicht die Bestimmung von h.

h = 6,62617·10^-34 J·s

2.12. Das Brechungsgesetz der Optik

Fällt ein Lichtstrahl auf eine Grenzfläche z.B. die zwischen Luft und Glas, dann wird er gebrochen. Das Verhältnis aus dem Sinus des Einfallswinkels α und dem Sinus des Brechungswinkels ß ist konstant. sin α / sin ß heißt Brechungsindex n. n ist von den Materialien abhängig, welche die Grenzfläche bilden. Das Brechungsgesetz kann mit Hilfe

Für sein y-Wert gilt: y = c_L ·t / cos α – x·tan α.

Wir denken uns nun noch ein in Richtung der x-Achse mit der Geschwindigkeit v bewegtes System S’. Die Achsen des zu diesem System gehörenden x’-y’-Koordinatensystem liegen zum Zeitpunkt t = t’= 0 auf denen des in der Abb. 2.12.1 sichtbaren Koordinatensystems. v kann so gewählt werden, dass die Wellenfront in S’ parallel zur x’-Achse verläuft. Dies ist dann der Fall, wenn das zu einem Punkt P der Wellenfront gehörende y' von x' unabhängig ist.

t = (t’+x’·v/c²) / k, x = (x’ + v·t) / k, y = c_L ·t / cos α – x·tan α

y = y’ = (c_L / cos α) ·(t’+x’·v/c²) / k – [(x’ + v·t’) / k ]· tan α

y’ = (c_L / cos α – v · tan α )·t’/ k + [(c_L / cos α) ·v/c² – tan α ]· x’ / k

Im Fall (c_L / cos α) ·v/c² – tan α = 0 verläuft die Wellenfront in S' parallel zur x'-Achse.

(c_L / cos α) ·v/c² – tanα = 0 → sin α = v · c_L/c²

Da in S’ die Wellenfront auch nach dem Eintritt in das Glas parallel zur x'-Achse bleibt, gilt eine entsprechende Gleichung auch für die gebrochene Welle im Glas.

sin ß = v · c_G/c² , c_G = Lichtgeschwindigkeit im Glas

sin α = v · c_L/c² ; sin ß = v · c_G/c²

↓

sin α / sin ß = c_L / c_G = n

2.13 Die Lichtinterferenz hinter einem Doppelspalt

Ein zur y-Achse paralleler Lichtstrahl ist auf einen Doppelspalt mit der Gitterkonstanten g gerichtet (siehe Abb. 2.13.1). Den beiden Spalten sind auf der x-Achse eines ruhenden Systems S die x-Werte – g/2 und + g/2 zugeordnet. Auf einem Bildschirm über den Spalten sind Lichtmaxima und Lichtminima (siehe Kapitel 1.13.5. ).

Ein zur y-Achse paralleler Lichtstrahl ist auf einen Doppelspalt mit der Gitterkonstanten g gerichtet (siehe Abb. 2.13.1). Den beiden Spalten sind auf der x-Achse eines ruhenden Systems S die x-Werte – g/2 und + g/2 zugeordnet. Auf einem Bildschirm über den Spalten sind Lichtmaxima und Lichtminima (siehe Kapitel 1.13.5. ).

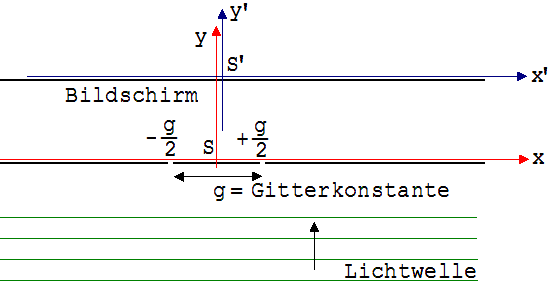
Abb. 2.13.1

Zum Verständnis dieser Erscheinung stellen wir uns ein x’; y’ - System S’ mit einer x’-Achse entlang des Bildschirms vor, welches mit der Geschwindigkeit v nach rechts fliegt. v ist so gewählt, dass die Lichtschwingungen (Schwingungszeit = T) in den beiden Spalten aus der Sicht von S’ gleiche Phasen haben.

Wellenberge, die aus der Sicht eines Beobachter in S' gleichzeitig zu einem Zeitpunkt t' im linken und rechten Spalt erscheinen, werden aus der Sicht von S als Wellenberge gesehen, die zu verschiedenen Zeitpunkten t₁ und t₂ mit dem zeitlichen Abstand n · T (n = 0; 1; 2; 3....) auf den Doppelspalt treffen.

t’ = [ t₁ – (v/c²) · (-g/2)] /k ; t’ = [ t₂ – (v/c²) · (g/2)] /k

t₁ – (v/c²) · (-g/2) = t₂ – (v/c²) · (g/2)   →   t₂ – t₁ = n · T = (v/c²) · g

c = λ/ T   →   T = λ /c

n · T = (v/c²) · g ; T = λ /c   →   n · λ = g · v/c

Aus der Sicht von S’ laufen zwei Wellenberge, die zum Zeitpunkt t’ die Spalten verlassen auf den Koordinatenursprung K₀’ des x’; y’ – Systems zu und erzeugen dort ein auch für ruhende Beobachter wahrnehmbares Intensitätsmaximum. Wenn die Wellenberge bei K₀’ eintreffen und dort ein Interferenzmaximum ausbilden, hat sich K₀’ aus der Sicht von S innerhalb einer Zeit t um x nach rechts bewegt. Das Intensitätsmaximum erscheint aus der Sicht von S deshalb im Abstand x von der y-Achse.

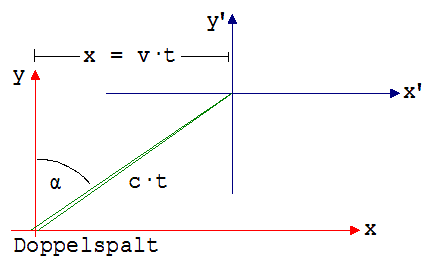
Abb. 2.13.2

n · λ = g · v/c

v/c = v·t / (c·t) = sin (α)

↓

n · λ = g · sin (α)

Für das Maximum 1. Ordnung (n = 1) gilt: λ = g · sin (α )

siehe Kapitel 1.13.5 !

2.14 Das Minkowski – Diagramm

Die Lorentztransformationen kann man so verändern, dass die Formeln für die Zeit t sich nicht mehr von denen für den Ort x unterscheiden. Man muss nur ein neues Zeitmaß einführen. Anstelle von t wird das Produkt c · t = m genommen. Mit m wird die Zeit durch den Weg beschrieben, den das Licht in dieser Zeit im Vakuum zurücklegt. Für v/c wird ß geschrieben.

Die ersten beiden Gleichungen in der dritten Spalte kann man zu der folgenden Vektorgleichung zusammenfassen.

{m; x} = m’ · (1/k)·{1; ß} + x’ · (1/k)·{ ß; 1}

(1/k)·{1; ß} = a; (1/k)·{ ß; 1} = b; |a| = |b|

Anhand dieser Gleichung kann man erkennen, wie man bei Kenntnis von m’ und x’ einen Punkt im Koordinatensystem mit den Koordinaten m und x findet. In Abb. 2.14.1 ist dies am Beispiel m’ = 4 Einheiten und x’ = 2 Einheiten dargestellt. (m; x) erreicht man vom Nullpunkt aus mit m’ Schritten der Länge |a| in Richtung von a und x’ Schritten der Länge |b| in Richtung von b. Man kann aber auch so vorgehen, wie dies in Abb. 2.14.2 angedeutet ist.

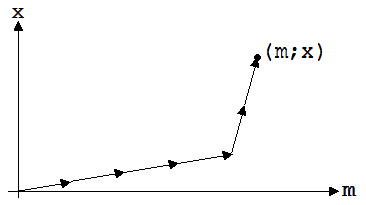
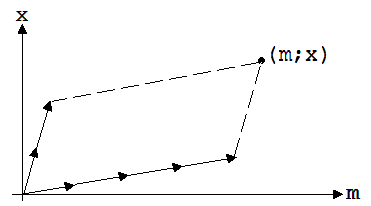
Abb. 2.14.1                                                 Abb.2.14.2

Die Abb. 2.14.2 regt zur Einführung eines schiefwinkligen Koordinatensystems an, auf deren Achsen eine Länge = |a| = |b| als Einheit betrachtet wird (siehe Abb. 2.14.3).

|a| = |b| = √[ (1 + ß²) / (1 - ß²) ]

tan α = ß = v/c; Steigung von (1/k)·{1; ß}!

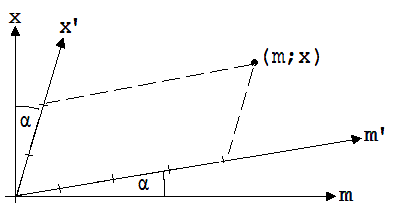
Abb. 2.14.3

Es ist erkennbar, wie zu dem Wertepaar m; x leicht die zugehörenden m’, x’ – Werte gefunden werden können. Die Punkte der x-Achse stellen Ereignisse dar, die im ruhenden System zum Zeitpunkt t = 0 stattfinden. Die Punkte der x’- Achse beschreiben Ereignisse, die sich im bewegten System zum Zeitpunkt t’ = 0 ereignen. Ereignisse am Ort x = 0 werden auf der m-Achse abgebildet, solche am Ort x’ = 0 auf der m’ –Achse.

2.15 Das Zwillingsparadoxon

Man denke sich Zwillinge A und B auf der Erde. B steige in eine Rakete und fliege mit 2/3 Lichtgeschwindigkeit durch den Weltraum. Nach einem Jahr komme er wieder nach Hause zu seinem Bruder. Da aus der Sicht von A alle Vorgänge in der Rakete zeitlich gedehnt werden, ist B dann weniger stark gealtert als A.

Man könnte nun folgende als Zwillingsparadoxon bekannte Erklärung abgeben:

A fliegt aus der Sicht von B mit 2/3 Lichtgeschwindigkeit. Was für B gilt muss auch für A gelten. Damit kommt man zu dem unsinnigen Schluss: Jeder der beiden Zwillinge ist biologisch jünger als sein Zwillingsbruder.

Die Aussage „Was für B gilt muss auch für A gelten“ trifft hier nicht zu, denn für B gehen die Uhren auf der Erde erst dann langsamer als die Raketenuhren, wenn er nach dem Beschleunigungsvorgang die Uhren in seiner Rakete synchronisiert. Zunächst sieht B nach dem Start seines Raumschiffs so wie sein Bruder die Raketenuhren in einer langsameren Gangart als die irdischen Uhren. Der Grund hierfür ist die Tatsache, dass die Uhren in der Rakete aus der Sicht von A während des Starts synchron bleiben und deshalb aus der Sicht von B nicht synchronisiert sind. Ist die Rakete in gleichförmiger Bewegung, dann kann B die Uhren in der Rakete synchronisieren. Nach einer solchen Synchronisation ordnet er beim Uhrenvergleich den Zeitangaben einer irdischen Uhr die Zeiten verschiedener Raketenuhren zu. Er liest die zugehörende Raketenzeit immer an der Uhr ab, an der die vorbeiziehende irdische Uhr gerade angelangt ist. Aus der Sicht des irdischen Beobachters ist dieser Uhrenvergleich nicht zulässig, weil nach seiner Sichtweise die zum Vergleich genommenen Raketenuhren nicht synchronisiert sind und deshalb falsche Zeiten anzeigen.

Es soll nun etwas genauer untersucht werden, wie B den Start seiner Rakete erlebt und welche Schlüsse er möglicherweise daraus zieht. Wir stellen uns einen sehr langen, rechteckigen Raum R innerhalb der Rakete vor (siehe Abb. 2.15.1), der während des Starts mit a auf die Geschwindigkeit v beschleunigt wird. In diesem Raum stehen Uhren, die unmittelbar vor der Beschleunigung zusammen mit den irdischen Uhren auf 0 eingestellt wurden. Während der Beschleunigung und danach zeigen diese Uhren aus der Sicht eines ruhenden Beobachters A gleiche Zeiten an.

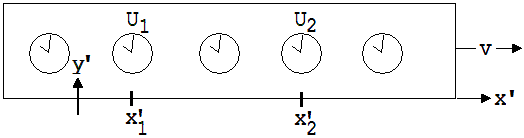
Abb. 2.15.1

Aus der Sicht von B geht nach der Beschleunigung auf die Geschwindigkeit v die Uhr bei x’₂ gegenüber der Uhr bei x’₁ um Δt’ = (v/c²)·Δx’ vor.

Δt’ = t’₂ - t’₁ ; Δx’ = x’₂ - x’₁

Beweis:

Wenn B die Uhren in der Rakete synchronisiert hat, dann gilt nach den Lorentztransformationen:

t = (t’₁ + x’₁ ·v/c²)/√(1-v²/c²);      t = (t’₂ + x’₂ ·v/c²)/√(1-v²/c²)

t’₁ und t’₂ sind die Zeiten, die der ruhende Beobachter A zu einer Zeit t seines Systems auf den Uhren U₁ und U₂ abliest.

Es werden Zeiteinstellungen und Koordinatensysteme in der Rakete und auf der Erde vorausgesetzt, wie sie den Lorentztransformationen zugrunde liegen.

(t’₁ + x’₁ ·v/c²) = (t’₂ + x’₂ ·v/c²)

Δt’ = t’₂ - t’₁ = - ( x’₂ - x’₁)·v/c²     →    Δt’ = -(v/c²)·Δx’

Aus der Sicht von A geht dann die Uhr bei x’₂ gegenüber der Uhr bei x’₁ nach. Da nach dem Start die Uhren aus der Sicht von A keine Zeitunterschiede zeigen, geht aus der Sicht von B die Uhr bei x’₂ gegenüber der Uhr bei x’₁ um (v/c²)·Δx’ vor.

Wir setzen nun voraus, dass sich B folgende Gedanken macht: Die im Raum R während des Beschleunigungsvorgangs der Dauer t’ wirkenden Kräfte sind keine Trägheitskräfte, sondern Gravitationskräfte, unter deren Wirkung der ruhende Beobachter A mit a’ in der Zeit t’ auf v = v’ beschleunigt wurde.

v = v’ = a’·t’

Diese Gravitationskraft ist für die unterschiedlichen Anzeigen der Uhren verantwortlich, sie bewirkt, dass die Uhr U₂ schneller geht als die Uhr U₁.

t’₂ = t’₁ + (v/c²) · Δx’; v = a’·t’     →     t’₂ = t’₁ · [ 1 + (a’/c²) · Δx’ ]

Für das Verhältnis der Taktfrequenzen t’₂ / t’₁ erhält er demnach:

t’₂ / t’₁ = 1 + (a’/c²) · Δx’

Geht man davon aus, dass man zwischen Trägheitskräften und Gravitationskräften hinsichtlich ihrer Wirkung keinen Unterschied feststellen kann, dann muss nach den Überlegungen von B eine Uhr U₂ die um h über einer Uhr U₁ im Gravitationsfeld der Erde aufgestellt ist, eine um t₂ / t₁ = 1 + (g/c²)·h schnellere Gangart haben als U₁.

Der in dieser Gleichung zum Ausdruck kommende Gangunterschied konnte mit hochgenauen Atomuhren nachgewiesen werden. Bei einem Höhenunterschied von 1000 m läuft die höhere Uhr während einer Stunde gegenüber der tieferen Uhr um 4·10^-10 Sekunden voraus.

Die hier beschriebene Tatsache lässt den Schluss zu, dass eine Lichtwelle eine Verminderung ihrer Frequenz erfährt (Rotverschiebung), wenn sie aus einem Gravitationsfeld aufsteigt. An höheren Orten laufen die Uhren schneller. Es wird dort eine größere Schwingungszeit und somit eine kleinere Frequenz gemessen. Auch diese Frequenzänderung konnte nachgewiesen werden.

Somit kann die Behauptung als zutreffend bezeichnet werden, dass in einem abgeschlossenen Raum zwischen Gravitations- und Trägheitskräften keine Unterschiede erkannt werden können, wenn diese durch äußere Umstände bedingt sind. Träge und schwere Masse sind äquivalent.

2.16 Historisches zur Entwicklung der Relativitätstheorie

Die Spezielle Relativitätstheorie hat viele Väter, die Allgemeine Relativitätstheorie ist das Werk Einsteins. Letztere basiert auf der schon von Ernst Mach formulierten Vorstellung, dass man Trägheitskräfte und Gravitationskräfte ohne Kenntnis ihrer Ursachen nicht unterscheiden kann. Wenn z.B. ein Mensch in einer großen Kiste aus großer Höhe frei zu Boden fällt und plötzlich eine Kraft spürt, weil er durch die Luft zu einer nahezu gleichförmigen Bewegung abgebremst wird, dann kann er in seiner Kiste nicht feststellen, ob es sich um eine Gravitations- oder eine Trägheitskraft handelt. Er kann auch die Auffassung vertreten, dass er aus einer gleichförmigen Bewegung beschleunigt wird. Demnach gelten in Räumen gleiche Gesetze, in denen weder Gravitations- noch Trägheitskräfte erfahren werden. Der letzte Satz ist eine Verallgemeinerung des schon früher formulierten Relativitätsprinzips.

Anmerkungen zur speziellen Relativitätstheorie im Lehrbuch für Theoretische Physik von Georg Joos (10. Auflage, 1959):

Die Zeittransformation hat bereits 1887 Voigt in einer wenig bekannten Arbeit vorgenommen. 1892 hat sie Lorentz für die Optik bewegter Körper aufgenommen. 1900 schrieb Lamor die Lorentz-Transformationen zuerst in der heute üblichen Form. 1904 erschien eine Arbeit von Lorentz, in der die Optik bewegter Körper ganz vom Standpunkt der Lorentztransformationen behandelt wurde. 1905 zogen unabhängig voneinander Poincarè und Einstein die folgenden Schlüsse aus den Lorentztransformationen:

1. Längenkontraktion und Zeitdilatation aus der Sicht bewegter Beobachter

2. Additionstheorem der Geschwindigkeiten

3. Dopplereffekt

Die Einsteinsche Arbeit enthielt darüber hinaus das fundamentale Gesetz der Trägheit der Energie.

Den Aussagen in dem genannten Lehrbuch ist noch hinzuzufügen, dass der österreichische Physiker Hasenöhrl schon 1904 ein auf nichtrelativistische Weise hergeleitetes Gesetz zur Trägheit der Energie veröffentlicht hat.

Das besondere Verdienst von Poincarè und Einstein für die Spezielle Relativitätstheorie ist der Beweis, dass die Lorentztransformationen im Einklang mit dem Relativitätsprinzip stehen. Erst als man sich darüber im Klaren war, was unter der Gleichzeitigkeit von Ereignissen zu verstehen ist (Synchronisation von Uhren), welche an verschiedenen Orten stattfinden, war die Voraussetzung für einen solchen Beweis gegeben. Einstein musste sich während seiner Tätigkeit im Berner Patentamt dieser Frage stellen. Anlass hierzu gaben Probleme bezüglich der Abfahrts- und Ankunftszeiten von Fernzügen -man denke an den Orientexpress.

Ausführliche Informationen über die Entwicklung der Relativitätstheorie enthält das Buch „Raffiniert ist der Herrgott ...“ von Abraham Pais (Vieweg-Verlag).

Diesem Buch ist zu entnehmen, dass Poincarè seine Arbeit am 5.6.1905 in der Académie des Sciences (Paris) vorstellte und Einstein seine Arbeit am 30.6.1905 in den Annalen der Physik veröffentlichte.