
1.9. Arbeit, Leistung, Energie
Arbeit

Abb. 1.9.1
Wird ein Gegenstand mit einer bestimmten Kraft F verschoben, dann spricht man von einer Arbeit W (work). Es erscheint sinnvoll, von einer Verdopplung der Arbeit zu sprechen, wenn entweder die Verschiebung s oder die Kraft F verdoppelt wird. Dieser Auffassung entspricht das Produkt F · s = W als Maß der Arbeit.
W = F · s; Einheit von W: N ·m = J (Joule)
Zur Verrichtung einer Arbeit können verschiedene Hilfsmittel herangezogen werden. Bekannte Hilfsmittel sind der Flaschenzug, die schiefe Ebene, der Hebel usw.. Ein Arbeitsmaß kann man nur dann als sinnvoll anerkennen, wenn sein Wert nur von den Zuständen vor und nach der Arbeit, nicht aber von der Art der Ausführung abhängt. So sollte die Arbeit W zum Anheben eines 10kg-Gewichts um 1m nicht davon abhängen ob das Gewicht mit Rolle und Seil oder stattdessen mit einem Flaschenzug hochgezogen wird. An den in der Abb. 1.9.2 skizzierten Aufzügen ist erkennbar, dass die Arbeit unabhängig vom verwendeten Hilfsmittel ist.
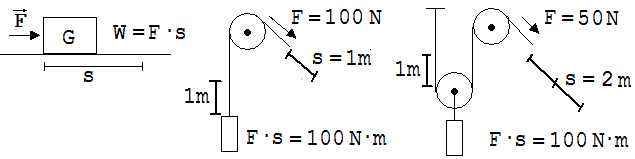
Abb. 1.9. 2
Bei der Definition des Arbeitsmaßes wurde zunächst daran gedacht, dass die Verschiebung und die Kraft gleiche Richtungen haben. Wenn die Kraft sich so verhält, wie dies in Abb.1.9.3 angedeutet ist, dann erscheint es sinnvoll zur Berechnung der Arbeit nur die Kraftkomponente Fp in Richtung der Verschiebung zu nehmen.
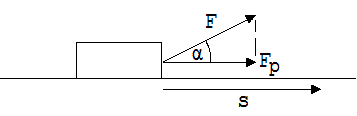
Abb. 1. 9.3
W = Fp · s ; Fp = F · cos(α)
↓
W = F · cos(α) · s = F · s· cos(α)
F · s· cos(α) ist das Skalarprodukt aus dem Kraftvektor F und dem Verschiebungsvektor s.
W = F· s = F1 · s1 + F2 · s2 + F3 · s3
Nach der hier gegebenen allgemeinen Definition des Arbeitsmaßes erhält man eine negative Arbeit, wenn die Kraft der Verschiebung entgegen gerichtet ist ( cos(α) < 0). Dies ist z.B dann der Fall, wenn jemand einen rollenden Wagen bremst.
Leistung
Eine Arbeit von z.B. 1000 J ist unterschiedlich zu bewerten, je nachdem ob sie in 10 s oder 1000 s verrichtet wird. Im ersten Fall wird von höherer Leistung gesprochen. Unter Leistung versteht man die in einer Zeiteinheit verrichtete Arbeit.
Leistung P(power) = W / t ; Einheit: Joule / Sekunde = Watt (W)
1.9.2 Energie (Perpetuum-Mobile)
Im den letzten Jahrhunderten wurde immer wieder der Bau eines „Perpetuum Mobile” versucht (manchmal geschieht dies auch heute noch)). Unter einem solchen Gerät versteht man eine periodisch arbeitende Maschine, die ohne Eingriffe von außen fortwährend Arbeit verrichtet. Bei oberflächlicher Betrachtung könnte man die in Abb. 1.9.4 skizzierte Anordnung für ein „Perpetuum Mobile” halten.
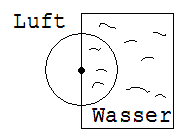
Abb. 1.9.4
Die eine Hälfte eines Holzrades befindet sich in einem mit Wasser gefüllten Behälter, die andere in Luft. Eine Gummidichtung in der Behälterwand schließt die Lücke zwischen dem Rad und der Behälterwand. Es könnte folgende Meinung vertreten werden:
Das Holzrad erfährt im Wasser einen Auftrieb, der eine Linksdrehung bewirkt. Leider ist diese Vorstellung falsch, denn bekanntlich wirken die durch den Wasserdruck bedingten Kräfte senkrecht zur Oberfläche und haben somit kein Drehmoment.
Die Erfolglosigkeit auf der Suche nach einem „Perpetuum Mobile” gab schließlich Anlass zu der Schlussfolgerung: Ein Perpetuum-Mobile ist unmöglich. Gleichwertig hiermit ist die Aussage :
Die Arbeit, die von einem System verrichtet werden kann, ist nur vom Anfangs- und Endzustand des Systems, nicht aber von der Art und Weise der Änderung abhängig. Die Arbeit, die von einem System beim Übergang von einem Zustand A in einen Zustand B verrichtet wird, nennen wir die Energie im Zustand A in Bezug auf den Zustand B. Der Satz von der Unmöglichkeit eines Perpetuum-Mobile wird immer wieder durch richtig Schlussfolgerungen bestätigt.
Ein Beispiel:
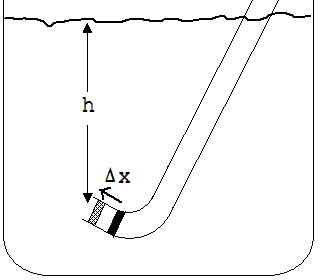
Abb. 1.9.5
Im Kapitel 1.6.4 wurde zur Berechnung des Wasserdrucks p in einer Wassertiefe h die Gleichung p = h ·g · ρ angegeben ( ρ = Dichte des Wassers). Bei der Herleitung wurde der Druck p auf eine parallel zur Wasseroberfläche liegende Fläche berechnet. Aus dieser Herleitung kann nicht geschlossen werden, dass die entwickelte Formel auch dann gilt, wenn die Fläche, die den Druck aufnimmt, eine andere Orientierung hat. Nun kann p = h·g·ρ ohne Beschränkung auf eine bestimmte Lage dieser Fläche hergeleitet werden. In ein Wasserbecken ist ein gebogenes Glasrohr eingetaucht, dessen eines Ende mit einem beweglichen Kolben (Querschnitt A ) abgeschlossen ist. Die Kraft F des Wassers auf diesen Kolben gleicht der Gegenkraft, die aufgebracht werden muss, um den Kolben in seiner Stellung zu halten. In Gedanken wird dieser Kolben bis zum Ende des Rohrs um ein kleines Stück Δx gegen das Wasser verschoben, wobei er eine geringe Wassermenge mit der Masse m verdrängt. Während die Arbeit W1 = F · Δx verrichtet wird, steigt der Wasserspiegel geringfügig an. Die gleiche Änderung des Wasserstandes ist auch in anderer Weise erreichbar: Bei festgehaltenem Kolben wird das Ende des Rohrs mit einem Schieber verschlossen und anschließend die vor dem Kolben stehende Wassermenge der Masse m mit der Arbeit W2 = m ·g · h zur Oberfläche gehoben.
Da die Arbeit nur vom Anfangs- und Endzustand abhängt gilt:
W1 = W2 → F · Δx = m ·g · h ; m = A ·Δx · ρ
↓
F · Δx = A ·Δx · ρ ·g · h → p = F/A = ρ ·g · h
Lageenergie
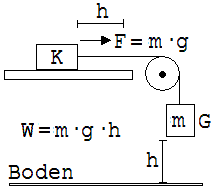

Abb. 1.9.6 Abb. 1.9.7
Ein Körper G der Masse m zieht einen Bremsklotz K gleichförmig über eine waagrechte Fläche. Die Bremskraft von K gleicht der Gewichtskraft von G. G verschiebt K nach einem leichten Stoß um die Strecke h und verrichtet hierbei die Arbeit W = m·g · h. G hat somit in Bezug auf den Boden die Energie E = m·g·h.
Spannungsenergie
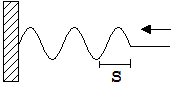

Abb. 1. 9.8 Abb. 1. 9.9
Eine um s gedehnte Schraubenfeder mit der Federkonstanten D wird mit der Hand langsam entspannt. Hierbei nimmt die Kraft von dem Wert D·s auf den Wert 0 ab. Die mittlere Kraft ist (D· s + 0)/2 = D · s/2. Während der Entspannung verrichtet die Feder die Arbeit W = (D·s/2)·s = ½·D· s2 . Sie hat demnach im gespannten Zustand die Energie E = ½·D· s2.
Bewegungsenergie (kinetische Energie)


Abb. 1. 9.10 Abb. 1. 9.11
Ein Wagen der Masse m und der Geschwindigkeit v wird mit Hilfe einer Fadenbremse -er wird durch eine Büroklammer gezogen - auf die Geschwindigkeit 0 abgebremst. Hierbei verrichtet er gegen den Faden die Arbeit W = F· s. F ist die Bremskraft und s der Bremsweg. Den Bremsweg s erhält man als Produkt aus der mittleren Geschwindigkeit v/2 und der Bremszeit t.
s = ½ · v · t; Bremskraft F = m· v/ t; → E = F · s = m ·v2/2
Ein besonders eindrucksvolles Experiment zur kinetischen Energie ist in der Abb.1.9.12 angedeutet.

Abb. 1.9.12
Ein Elektromotor dreht einen Eisenzylinder ( m = 420 g, r = 3cm) auf ca. 100 Hz. Anschließend werden die Anschlüsse des Motors mit einem Glühbirnchen verbunden. Dieses leuchtet dann ungefähr eine Minute lang. Rotierende Zylinder werden bei Experimenten zur Kernfusion zur kurzzeitigen Erzeugung derart hoher elektrischer Leistungen eingesetzt, die nicht aus dem Leitungsnetz entnommen werden können.
Welche kinetische Energie hat der in der letzten Abbildung sichtbare Zylinder bei 100 Umdrehungen pro Sekunde ?
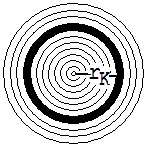
Abb. 1.9. 13
Zur Berechnung dieser Energie denken wir uns den Zylinder (siehe Abb. 1.9.13) mit dem Radius R , der Masse m und der Länge L in n konzentrische, dünnwandige Hohlzylinder mit den Radien rK und der Wanddicke d = R/n eingeteilt (Bsp.: n = 1000). Für die Rotationsenergie e eines solchen Hohlzylinders mit der Masse mK, dem Radius rK und der Rotationsgeschwindigkeit vK gilt:
e = mK · vK2/2; vK = Geschwindigkeit eines Punktes auf dem Hohlzylinder
vK = 2 ·π · rK / T ; T = Umdrehungszeit → vK = (2 ·π / T ) · rK; (2 ·π / T ) ist die Winkelgeschwindigkeit ω.
In der Zeit T dreht sich der Zylinder um den Winkel 2 ·π (Bogenmaß).
e = mK · vK2/2, vK = ω · rK → e = mK ·(ω · rK)2 / 2 = mK ·rK2 · ω2 /2
Wenn wir die Hohlzylinder mit den Zahlen von 1 bis n durchnummerieren, dann können wir für die gesamte Rotationsenergie schreiben:
ERot = (m1·r12 + m2·r22 + m3·r32 ....................+ mn·rn2 ) · ω2 /2
Die Summe (m1·r12 + m2·r22 + m3·r32 ....................+ mn·rn2 ) heißt Trägheitsmoment J.
↓
ERot = J·ω2 / 2
Für einen Zylinders mit der Masse m und dem Radius R gilt: J = ½· m · R2
Der Zylinder in der Abb.1.9.12 hat demnach das Trägheitsmoment J = 0,5·0,42kg·(0,03 m)2 = 0,000189 kg· m². Seine kinetische Energie bei 100 Hz ist J·ω2 / 2 = 0,000189 kg· m² · (2·π·100 Hz)2 / 2 = 37 Joule.
Herleitung von J = ½· m · R2
Der Zylinder wird in Gedanken in 1000 Hohlzylinder mit der Wandstärke R/1000 eingeteilt. Für das Trägheitsmoment j eines solchen dünnwandigen Hohlzylinders mit dem Radius rK und der Masse mk gilt: j = mK · rK2 ; mK = 2·π ·rK ·L· (R/1000) ·ρ; ρ = Dichte des Materials
Das Volumen eines dünnwandigen Hohlzylinders kann als Produkt von Oberfläche und Wanddicke dargestellt werden.
↓
j = 2·π·rK·L· (R/1000)·ρ·rK2 = 2·π·rK3 ·L·(R/1000)·ρ = 2·π· L·ρ·R4 ·(rK /R)3/1000
Das Gesamtträgheitsmoment J des Vollzylinders erhalten wir durch Summation der einzelnen j.
J = 2· π· L · ρ ·R4 ·[(r1/ R)3 + (r2/ R)3 + (r3/ R)3 ........] /1000 = 2· π· L · ρ ·R4 [(1/ 1000)3 + (2/1000)3 +(3/1000)3........]/1000
n = 1000; r1 = R/n ; r2 = 2· R/n; r3 = 3· R/n……
rk/ R haben die Werte 1/1000, 2/1000, 3/1000 .........1000/1000
Die Berechnung der Summe [(1/ 1000)3 + (2/1000)3 +(3/1000)3........] geschieht mit dem Open-Office-Tabellenkalkulationsprogamm ( Tabelle 13 ). 250 ist das Ergebnis . [(1/ 1000)3 + (2/1000)3 +(3/1000)3........]/1000 ist demnach 1/4.
↓
J = 2· π· L · ρ ·R4 /4 = (1/2) ·(π·R2· L · ρ) ·R2 ; π·R2· L · ρ = m → J = (½) · m · R2
Anmerkung: Zur Berechnung von J sollten statt der Innenradien rK der Hohlzylinder Werte genommen werden, der zwischen den äußeren und inneren Radien liegen. Der durch rK verursachte Fehler geht jedoch mit kleiner werdender Wanddicke gegen 0.
1.9.4 Satz von der Erhaltung der Energie
Die Arbeit, die von einem System von Gegenständen verrichtet wird, hängt nur vom Anfangs- und Endzustand dieses Systems ab.
Dies lässt folgenden Schluss zu:
In Bezug auf die Energieänderung eines Systems S ist es gleichgültig ob man S sofort von einem Zustand A in einen Zustand B überführt, oder ob man S sich einige Zeit selbst überlässt und dann in den Zustand B bringt. In beiden Fällen wird die gleiche Energie abgegeben. Daraus folgt, dass bei Wechselwirkungen innerhalb des Systems die Gesamtenergie unverändert bleibt. Somit können wir sagen:
In einem abgeschlossenen System bleibt die Energie erhalten (Satz von der Erhaltung der Energie).
Der Energieerhaltungssatz erscheint ungültig, wenn eine Bewegung durch Reibung beeinträchtigt wird. Denkt man jedoch an den atomaren Aufbau der Materie, dann liegt die Vermutung nahe: Bei Reibung wird die Energie der Atome vermehrt, die hierbei verursachte Erwärmung ist ein Zeichen für höhere Atomgeschwindigkeiten.
1.9.5 Anwendungsbeispiele zum Energieerhaltungssatz
1.9.5.1 Kinetische Energie eines fallenden Gegenstandes
Es soll unter Anwendung des Energieerhaltungssatzes die Geschwindigkeit v berechnet werden, mit der ein aus der Höhe h fallender Körper K die Erde trifft. Die Erde E und der Körper K bilden in diesem Fall ein abgeschlossenes System.
Es gilt: m ·g ·h = mK ·vK2 / 2 + mE·vE2 / 2
Gesamte kinetische Energie = kinetische Energie von K + kinetische Energie der Erde !
Die linke Seite der Gleichung steht für die Lageenergie (potentielle Energie) vor dem Fall, die rechte für die gesamte kinetische Energie danach. Unter Anwendung des Impulssatzes können wir zeigen, dass die kinetische Energie der Erde vernachlässigt werden kann.
mE · vE = mK ·vK → vE = (mK / mE ) · vK
↓
mE · vE2 / 2 = mE ·(mK / mE )2 ·vK2 / 2 = mK ·(mK / mE ) · vK2 / 2
vE und vK sind Geschwindigkeitsbeträge
mE · vE2 / 2 << mK · vK2 / 2 → mK ·h ·g = mK · vK2 / 2 → h ·g·2 = vK2
vK = √(h ·g·2)
1.9.5.2 Rollbewegung auf einer schiefen Ebene
Wir lassen einen massiven Zylinder Z ( m = 200g) mit dem Radius R und der Länge L und anschließend einen gleich schweren Wagen W die um α geneigte Experimentierwippe herab rollen. In beiden Fällen wird vor der Drehung um α ein für das Experimentierobjekt passender Reibungsausgleich durchgeführt. An den s-t-Diagrammen in Abb. 1.9.14 ist erkennbar, dass der Wagen einen Weg s in kürzerer Zeit zurücklegt als der Zylinder.
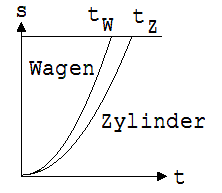
Abb. 1. 9.14
Die Momentangeschwindigkeiten am Ende des Weges erhalten wir nach v = 2·s/t (gleichförmig-beschleunigte Bewegung). t ist die Zeit zum Weg s. Aus den am Diagramm ablesbaren Werten folgt:
vZylinder / vWagen = (2· s/ tZ) / (2· s/ tW) = tW /t Z = 0,81
Diese Tatsache verleitet zu dem Schluss:
EnergieZylinder / EnergieWagen = vz2 /vW2 = 0.812 = 0,6561 ≈ 2/3
Die Zylinderenergie erscheint um 1/3 kleiner zu sein als die kinetische Energie des Wagens. Dies steht im Widerspruch zum Energieerhaltungssatz, denn die kinetischen Energien werden beim Durchlauf gleicher Höhendifferenzen angenommen.
Verständlich wird diese Tatsache dann, wenn man bedenkt, dass der Zylinder durch zwei Bewegungsformen ausgezeichnet ist. Während sich der Schwerpunkt mit v bewegt (Translation), rotiert der Zylinder um eine durch den Schwerpunkt laufende Achse. Auf diese Rotation entfällt offensichtlich 1/3 der Gesamtenergie.
Die Rotationsenergie fällt als zusätzliche Energie dann auf, wenn man den rollenden Zylinder an einer durch seine Mitte geführten Achse von der Bahn abhebt und die Achse ruhig hält. Der Zylinder rotiert nach diesem Bremsvorgang weiter.
Nach 1.9.3 gilt: ERot = J · ω2 / 2 = J · (v/R)2 / 2 = ( J/R2 ) · v2/ 2
ω = Geschwindigkeit v des Zylinderschwerpunkts / R.
Dies ist leicht einzusehen, wenn man bedenkt, dass sich der Zylinder während einer Drehung in der Zeit T um 2·π·R fortbewegt.
v = 2·π· R / T = (2·π/T) · R = ω · R.
ERot = ( J/R2 ) · v2/ 2 , J = ½ ·m·R2 → ERot = m · v2 / 4
Dies entspricht den oben angegebenen Versuchsergebnissen.
ERot = m · v2 / 4 ist 1/3 der Gesamtenergie E = ETranslation + Erot = m · v2 / 2 + m · v2 / 4.
Welchen Einfluss hat das Trägheitsmoment auf die Beschleunigung eines rollenden Gegenstands ?
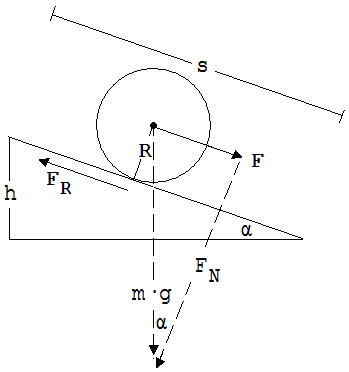
Abb. 1.9.15
Wir denken uns einen zunächst ruhenden Zylinder Z (Radius R, Masse m), der auf einer schiefen Ebene eine Strecke s herab rollt, dabei h an Höhe verliert und die Geschwindigkeit v erreicht.
m · g · h = m · v2 /2 + ( J/R2 ) · v2/ 2 ; m · g · h = v2 ·(m + J/R2 ) / 2; h = s ·sin α; m · g · h = m · g · s · sin α
m · g · sin α ist die Hangabtriebskraft F
m · g · s · sin α = F · s
F·s = v2 ·(m + J/R2 )/2; s = ½ · a · t2 ; v = a·t
↓
F ·½ · a · t2 = (a · t)2 · (m + J/R2 ) / 2
↓
F = a · (m + J/R2 ) → F - a · J/R2 = a · m
Da die Summe aller auf den Zylinder einwirkenden Kräfte gleich dem Produkt m · a ist, wird mit der letzten Gleichung angezeigt, dass der Hangabtriebskraft eine Kraft FR = a · J/R2 entgegen wirkt. Diese Kraft muss von der Rollbahn ausgehen (siehe Abb. 1. 9.15). Sie ist für die Drehung maßgebend. Man könnte sie durch Glätten der Rollbahn vermindern und hätte dann eine Rutschbewegung.
FR = a · J/R2 ; J =½ ·m·R2 → FR = ½ · m · a
Lässt man statt des Zylinders eine Eisenkugel eine schiefe Ebene hinab rollen, dann ist zu erfahren, dass FR = a · J/R2 = 2/5· m · a ist. Das Trägheitsmoment der Kugel ist nach J/R2 = 2/5· m gleich J = 2/5· mKugel · R2.
1.9.5.3 Über das Auslaufen einer Badewanne
Eine quaderförmige Badewanne mit dem Querschnitt A = 0,8 m² läuft durch eine Öffnung am Boden mit dem Querschnitt B aus.
B = 10 cm2 = 0,001 m2 Anfängliches Wasservolumen = 0,15 m³.

Abb. 1. 9.16
1. Mit welcher Geschwindigkeit tritt das Wasser aus dieser Öffnung ?
2. In welcher Zeit wird die Badewanne geleert ?
Diese beiden Fragen können mit Hilfe des Energiesatzes beantwortet werden. Auf die Frage 1 ist schnell eine Antwort gefunden. Wenn eine kleine Wassermenge der Masse m’ ausläuft, dann wird sie an der Oberfläche des Wassers vermisst. Die potentielle Energie des Wassers nimmt um m’·g ·x ab (x = Höhe des Wasserspiegels). Das unten austretende Wasser hat die kinetische Energie m’ ·v2 /2 . Nach dem Energieerhaltungssatz gilt:
m’ ·v2 /2 = m’ · g · x → v = √( 2 · g · x )
Die anfängliche kinetische Energie des Wassers infolge der Sinkgeschwindigkeit ist vernachlässigbar klein. Aus dem Wasservolumen V und dem Querschnitt A der Badewanne kann x errechnet werden.
x ·A = V → x = V/A
v = √( 2 · g · x) → v = √( 2 · g · V/A )
Nun kann auch die 2. Frage beantwortet werden.
v· Δt · B = √( 2 · g · V/ A ) · Δt · B ist das Volumen des Wassers, welches in einem kleinen Zeitabschnitt Δt aus der Wanne fließt (siehe Abb. 1.9.17).
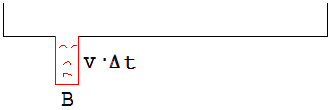
Abb. 1.9.1
Vnach Δt = Vvor Δt – √( 2 · g · VvorΔt / A ) · Δt · B
Mit dieser Gleichung kann eine Tabelle für die Volumina zu verschiedenen Zeit-punkten während der Entleerung angelegt werden.
Die Abb. 1.9.18 ist das zugehörende Diagramm. Es ist zu sehen, dass eine Wanne mit einem Querschnitt A = 0,8 m2, welche anfangs 0,15 m3 Wasser enthält, in ca. T = 156 s durch ein Loch mit dem Querschnitt B = 10 cm2 leer läuft. Vermutlich handelt es sich bei diesem Diagramm um eine Parabel, welche durch eine Funktionsgleichung der Form V= f·(t-T)2 beschrieben wird.
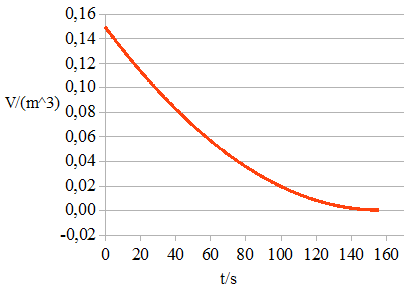
Abb. 1. 9.18: Tabelle 14
Beweis: Vnach Δt - Vvor Δt = ΔV ≈ – √( 2 · g · VvorΔt / A ) · B · Δt
dV/dt = – √( 2 · g · V / A ) · B → dt/dV = - √(A/( 2 · g· B2)) · V -½
Auf der Suche nach einer Funktion t(V) mit dt/dV = - √(A/( 2 · g· B2)) · V -½ finden wir: t = - √(A/( 2 · g· B2)) · 2 ·V ½ + Konstante C
Bei V = 0 ist t = T . Folglich gilt: C = T
t = - √(A/( 2 · g· B2)) · 2 ·V ½ + T → (t-T)2 = A/( 2 · g· B2 ) · 4·V
V = (t-T)2 · g· B2/ (A · 2) → V = f · (t-T)2, f = g· B2/ (A · 2)
V0 = f · T2 → T = √(V0 / f)
Für den hier beschriebenen Fall gilt: f = g· B2/ (A · 2) = 6,131· 10-6 m³/s2 → T = 156 s
Die hier gemachten Aussagen können leicht experimentell auf ihre Richtigkeit geprüft werden. Zu empfehlen ist eine Messanordnung, wie sie in der Abb. 1.6.15 auf der Seite 50 zu sehen ist. Statt des dort abgebildeten Gefäßes mit textilem Boden ist eine Dose mit einem Loch im Gefäßboden zu nehmen.