1.8 Schwingungen
1.8.1 Die Harmonische Schwingung

Abb. 1.8.1
Siehe https://www.youtube.com/watch?v=wlnEcwHaJmM
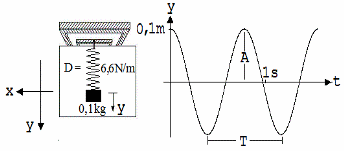
An der Vorderseite der Wippe wird eine Schraubenfeder mit einem Körper G der Masse m = 0,1 kg aufgehängt. Nachdem sich G beruhigt hat, wird er nach unten gezogen und anschließend zum Schwingen freigegeben. Mit der Wippe wird die Federkraft D·(s+y) gemessen. D ist die Federkonstante, s die Federdehnung bei ruhendem Körper, und y ist die Abweichung von der Ruhelage, die nach unten positiv und nach oben negativ gewertet wird. Als Zeitachse wird eine Gerade gewählt, die den Verlauf des Diagramms bei einer ruhenden Feder anzeigt. Damit wird ein Diagramm erhalten, welches D·y in Abhängigkeit von der Zeit darstellt. Schreibt man an die senkrechte Koordinatenachse anstelle der Kräfte die zugehörigen y-Werte, dann hat man ein Weg-Zeit-Diagramm.
G wird unter der Kraft Fy = - D·y mit ay = -D·y/m beschleunigt. Das - Zeichen zeigt an, dass die Kraft der Auslenkung entgegen gerichtet ist. Bei genauer Prüfung des Sachverhalts wird man schreiben: Fy = m·g - D·(s+y). s ist die Dehnung der Feder in ihrer Ruhelage. Fy = - D·y gilt, weil in der Ruhelage die Gewichtskraft m·g durch die Federkraft D·s ausgeglichen wird.
Fy = -D·y → - D·y = m·ay → ay = - (D/m)·y
Elongation, Amplitude, Schwingungszeit und Frequenz sind Begriffe, die bei der Behandlung von Schwingungen zu hören sind.
1. Elongation y: Sie ist die augenblickliche Abweichung von der Ruhelage.
2. Amplitude A: Sie ist der Betrag der maximalen Elongation.
3. Schwingungszeit T: Dies ist die Zeit, die während einer Schwingung vergeht.
4. Frequenz f: f = n/t, n ist die Zahl der Schwingungen in der Zeit t.
Aus t = n·T folgt: f = n/(n·T) = 1/ T. Die Frequenz gibt die Anzahl der Schwingungen pro Zeiteinheit an, sie gleicht dem Kehrwert der Schwingungsdauer. Für die zugehörende Einheit 1/s schreibt man auch Hz. Hz steht für den Nachnamen des Physikers Heinrich Hertz.
Lässt man eine Kugel K in einer auf der Wippe stehenden Schale rotieren, dann wird vom Rechner ein Diagramm gezeichnet, welches man auch einer Federschwingung zuordnen könnte (siehe Abb. 1.8.2).
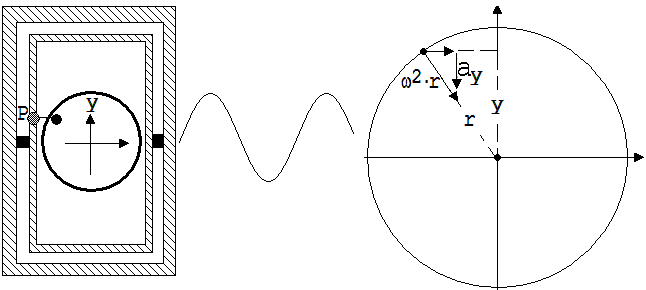
Abb. 1. 8.2 Abb. 1. 8.3
Bewegt sich die Projektion P einer gleichförmig kreisenden Kugel K auf die Längsseite der Wippe wie ein an einer Schraubenfeder hin und her schwingender Körper G ?
Wenn dies so ist, dann müsste so wie für G auch für eine gleichförmig rotierenden Kugel gelten: ay ~ y. Dies ist leicht anhand der Abb.1.8.3 beweisbar. ay ist die y-Komponente der Kreisbeschleunigung ω2·r.
-ay / (ω2 ·r) = y/r → ay = - ω2·y
Daraus folgt: Ist die Winkelgeschwindigkeit ω der kreisenden Kugel so gewählt, dass ω2 ·y = D·y/m ↔ ω2 = D/m gilt, und haben P und das an einer Feder schwingende Gewicht G gleichzeitig eine maximale Auslenkung in gleicher Größe, dann stimmen die Elongationen von P und G in jedem Augenblick infolge gleicher Beschleunigungen überein. In diesem Fall dreht sich die Kugel in der Schwingungszeit T um den Winkel 2·π.
2·π/T = ω = √(D/m) → T = 2·π ·√(m/D) → f = [1/(2·π)]·√(D/m)
Elongation, Geschwindigkeit und Beschleunigung als Funktionen der Zeit
Man kann eine Schwingung mit einem gleichförmig rotierenden Körper K beschreiben, dessen Projektion auf die Schwingungsbahn mit dem schwingenden Körper hin und her geht. Statt eines solchen Körpers K kann man auch einen mit ω = √(D/m) rotierenden Zeiger nehmen, dessen orthogonale Projektion auf die Schwingungsbahn die Elongation anzeigt (siehe Abb. 1.8.4). Die Winkelgeschwindigkeit ω des zugeordneten Zeigers heißt Kreisfrequenz der Schwingung. Wenn der mitlaufende Zeiger der Länge A den Winkel φ mit der durch den Schwingungsmittelpunkt laufenden x-Achse bildet, dann wird die Stoppuhr auf 0 gestellt. Zu einem späteren Zeitpunkt t bildet der Zeiger den Winkel ω·t + φ mit der x-Achse. Für die Auslenkung y (Elongation) gilt dann:
y = A · sin(ω·t + φ); ω·t + φ heißt Phasenwinkel (Winkel im Bogenmaß !)
Die hier aufgestellte Bewegungsgleichung ist nur dann richtig, wenn die beschleunigende Kraft F der Auslenkung proportional ist. Man spricht in diesem Fall von einer harmonischen Schwingung.
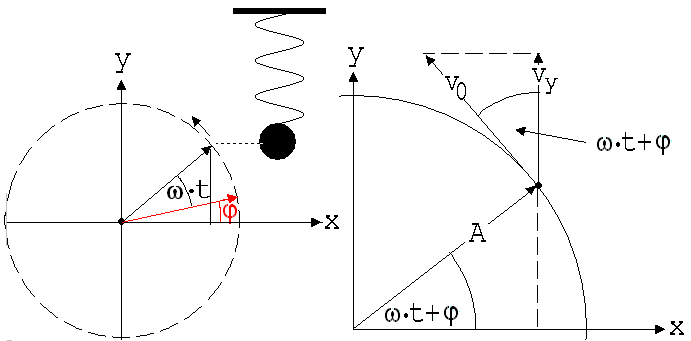
Abb. 1.8.4 Abb. 1.8.5
An der Abb. 1.8.5 ist zu sehen, wie die Geschwindigkeit des schwingenden Körpers berechnet werden kann. Diese Geschwindigkeit vy ist gleich der Vertikalkomponenten von v0, der Geschwindigkeit der rotierenden Zeigerspitze.
vy = v0 · cos(ω·t + φ); v0 = ω·A → vy = dy/dt = A ·ω· cos(ω·t + φ)
Für die Beschleunigung ay gilt: ay = - ω2·y
ay = - ω2·y; y = A · sin(ω·t + φ) → ay = dvy /dt = -A · ω2· sin(ω·t + φ)
Folgende Regeln sind erkennbar:
1. Den Differentialquotienten von einer Funktion der Form „Konstante · sin(ω·t + φ)“ erhält man, indem man sin durch cos ersetzt, und den dann vorliegenden Term mit dem bei t stehenden Faktor multipliziert.
2. Den Differentialquotienten von einer Funktion der Form „Konstante · cos(ω·t + φ)“ erhält man, indem man cos durch - sin ersetzt, und den dann vorliegenden Term mit dem bei t stehenden Faktor multipliziert.
Damit noch einmal deutlich wird, wofür ein Differentialquotient steht, wird der zur Funktion f(t) = A·cos(ω·t + φ) gehörende Differentialquotient mit Blick auf die Abb. 1.8.6 hergeleitet.
Abb. 1.8.6
A·{cos[ω · (t +Δt) + φ] – cos[ω · t + φ]} = Δf(t)
Δf(t) = -s · sin(β ) = - s·sin ( ω · t + φ)
Δf(t)= - [s/(A · ω · Δt)] · (A · ω · Δt)· sin (ω · t + φ)
Δf(t) /Δt = - [s/(A · ω · Δt)] · A ·ω ·sin (ω · t + φ)
Strebt Δt gegen 0 dann nähert sich der Quotient s/ (A · ω · Δt) dem Grenzwert 1.
A·ω· Δt ist der Bogen zum Winkel α = ω · Δt !
↓
d(f(t) / dt = lim Δt→ 0 A·{cos[ω · (t + Δt) + φ]-cos[ω · t + φ]}/ Δt = - A·ω ·sin ( ω · t + φ)
Die Glasplatte der Wippe schwingt nach einem Stoß mit T = 0,1 s bei stark abklingender Amplitude hin und her (siehe Abb. 1. 8.7). Wegen ihrer Amplitudenabnahme, sie erfolgt hier nach einer Exponentialfunktion, nennt man diese Schwingung gedämpft.
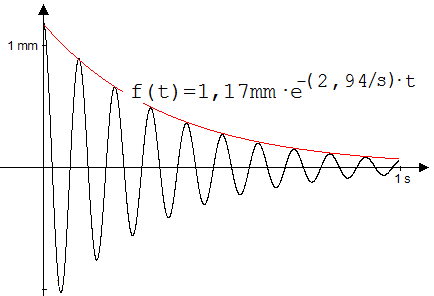
Abb. 1. 8.7
Ebenfalls stark gedämpft ist das Hin- und Herschwappen von Wasser in einer Wanne (Abb. 1.8.8) oder das Schwingen einer Wassersäule in einem U-Rohr (siehe Abb. 1.8.9 ).

Abb. 1.8.8 Abb. 1.8.9
In der Abb. 1.8.9 ist ein bis zu den weißen Markierungen mit Wasser gefülltes U-Rohr zu sehen. Auf dem rechten Schenkel sitzt ein Stopfen, durch den ein Glasrohr geführt ist. Wird mit einem an das Glasrohr angeschlossenen Schlauch in das U-Rohr hinein geblasen, dann stellt sich in den beiden Schenkeln ein verschieden hoher Wasserstand ein. Nach Freigabe der Schlauchöffnung schwingt das Wasser mit abnehmender Amplitude hin und her. Die Dämpfung der Schwingung kann mit einer am Schlauch angebrachten Klemme geregelt werden. Je mehr der Schlauch zusammen gequetscht ist, desto größer ist die Dämpfung. Bei sehr großer Dämpfung schwingt das Wasser nicht mehr um die Ruhelage, es nähert sich ihr einseitig aperiodisch an (siehe Abb. 1.8.10).
Abb. 1.8.10
Ist die aperiodische Bewegung so, dass bei geringfügiger Verminderung der Dämpfung wieder eine gedämpfte Schwingung erkennbar ist, dann spricht man vom aperiodischen Grenzfall. Für schwingungsfähige Anzeigeteile von Messinstrumenten, zum Beispiel für den Zeiger eines Amperemeters, wird dieser aperiodische Grenzfall als Bewegungsform angestrebt, weil mit ihm die schnellste Einstellung auf den Messwert erfolgt.
Das Schwingungsverhalten eines Federpendels mit einer der Geschwindigkeit proportionalen Reibungskraft FR= -k·v kann mit einem Open-Office-Tabellenkalkulationsprogramm etwas genauer untersucht werden. In der Abb. 1.8.11 sind Bewegungsdiagramme zu sehen, die mit einem solchen Programm berechnet wurden. Vorausgesetzt wurde ein 1kg-Körper an einer Feder mit D = 1kg/s2, der sich unter der Kraft Fy = -D·y - k·v entlang der y-Achse eines Koordinatensystems bewegt.
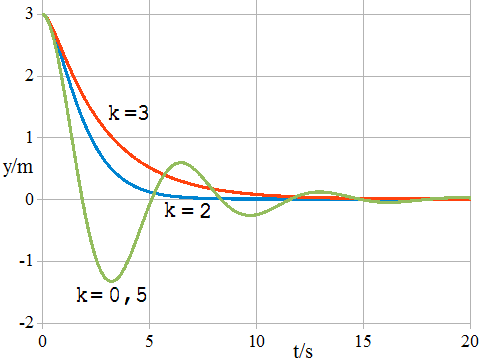
Abb.1.8.11 Tabelle 7
Für die Anfangswerte von y und v wurden die Werte 3 m, und 0 m/s bestimmt. Die Diagramme sind den k-Werten 0,5kg/s, 2 kg/s und 3kg/s zuzuordnen. k = 2 kg/s liefert den aperiodischen Grenzfall.
Zur Berechnung dieser Diagramme ist folgendes anzumerken:
Die Kraft Fy = F2 = -D·y - k·v wird unter B in die zum schiefen Wurf mit Reibung angelegte Tabelle eingetragen. In die 3. Zeile der Spalte B schreiben wir „= -$K$2*J2-$N$2*F2“ und kopieren diese Zeile in 2000 darunter liegende Zeilen dieser Spalte. Als Anfangswerte werden für y und v2 die Werte 3 (3 m) und 0 bestimmt. Für D und m werden in den Spalten K und M die Werte 1 (1kg und 1 kg/s2) eingetragen. Für k wird in der Spalte N zunächst 0,5 (0,5 kg/s) eingesetzt. Ist die Berechnung mit k=0,5 durchgeführt, dann werden die y-Werte auf folgende Weise in die Spalte Q übertragen. In die 2. Zeile von Q wird =J2 geschrieben und die Eingabe mit der Taste „Zeilenwechsel“ abgeschlossen. Anschließend wird diese Anweisung in 2000 darunter liegende Zeilen kopiert. Damit nach Wahl eines anderen k-Werts z.B. k=2 in der Spalte Q die zu k = 0,5 gehörenden Werte stehen bleiben und nicht durch die zu k=2 gehörenden Werte ersetzt werden, wird der Kopf dieser Spalte (Q) und dann unter „Daten“ die Anweisung „Text in Spalten..“ angeklickt. Auf diese Weise erreicht man, dass die Zahlen unter Q bei neuen Berechnungen keine Änderungen erfahren. So wie mit k = 0,5 verfährt man anschließend mit k = 2 und k=3. Die zu diesen k-Werten gehörenden y-Werte werden mit =J2 in die Spalten R und S übertragen. In die Spalte P werden mit =H2 die Zeitwerte übertragen.
Zum Anlegen der Weg-Zeitdiagramme werden die Spalten P,Q,R und S ausgewählt. Dann wird nach Anklicken von „Diagramm“ unter „Einfügen“ die Anweisung zum Zeichnen der Diagramme (XY, Nur Linien) gegeben.
1.8.3 Das Fadenpendel
Wie in Abb. 1.8.12 erkennbar, schwingt ein Fadenpendel über der Experimentierwippe an einem auf ihr befestigten Stab. Bewegt sich der Pendelkörper nahe der Glasplatte, dann erhält man bei kleinen Auslenkungen ein x-t-Diagramm des schwingenden Körpers. Die Schwingungszeit für kleine Amplituden kann ohne Schwierigkeiten berechnet werden (siehe Abb. 1.8.13), wenn zunächst angenommen wird, dass die Schwingung harmonisch ist. Zur Ermittlung von D muss die zurücktreibende Kraft F zu einer Auslenkung x bestimmt werden. Die für die Schwingung verantwortliche Erdanziehungskraft m · g verhält sich in Bezug auf den schwingenden Körper G wie ihre beiden in der Skizze angedeuteten Komponenten F und FL .
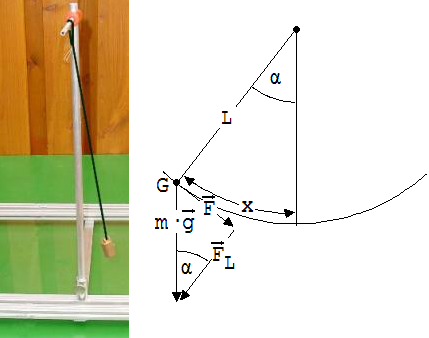
Abb. 1.8.12 Abb. 1.8.13
F ist die zurück treibende Kraft.
Für ihren Betrag gilt: F = m ·g · sin α
Als Auslenkung x (Kreisbogen) erhalten wir: x = L · α (α = Winkel im Bogenmaß)
F/x = D = m · g · sin α /(L ·α)
Die letzte Gleichung zeigt, dass die Schwingung nicht harmonisch ist. Beschränkt man sich jedoch auf kleine Auslenkungen x, dann kann sin α durch α ( Bogenmaß !) ersetzt werden. → D ≈ m·g/L. Demnach kann die Schwingung bei kleinen Auslenkungen als harmonisch bezeichnet werden.
T = 2·π·√(m/D); D = m·g/L → T = 2·π·√(L/g)
In der Abb. 1.8.14 sind drei zu den Amplituden 0,1 m, 0,5 m und 0,75 m mit dem Open - Office-Tabellenkalkulationsprogramm errechnete Schwingungsdiagramme zu sehen, welche die Elongation x eines 0,5 m langen Pendels in Abhängigkeit von der Zeit darstellen. Zur Berechnung dieser Diagramme wurde die für Federschwingung aufgestellte Tabelle geändert. Als F1= Fx wurde F = m · g · sin(x/L) eingetragen.
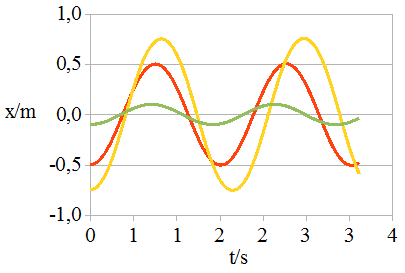
Abb. 1.8.14 Tabelle 8
Zur Verbesserung der Rechengenauigkeit wurde für Δt der Wert 0,0005 s gewählt und die Zahl der Tabellenzeilen entsprechend auf 6400 Zeilen vergrößert. Es ist zu sehen, dass mit zunehmender Amplitude die Diagramme von einer Sinusform mehr und mehr abweichen und die Schwingungszeit größer wird.
1.8.4 Die Schwebung
Lässt man zwei Fadenpendel verschiedener Frequenz am gleichen Halter über der Mitte der Experimentierwippe pendeln (siehe Abb. 1.8.15), dann wird ein Schwebungsdiagramm aufgezeichnet. Die Pendel üben auf ihren Halter periodisch schwankende Kräfte aus, die zusammen eine als Schwebung bekannte Schwingungsform ergeben. Minima und Maxima entstehen dann, wenn die Pendel gegeneinander bzw. miteinander schwingen.

Abb. 1.8.15
Im Hinblick auf diese Erscheinung ist das akustische Schwebungsphänomen (Signal mit periodisch schwankender Lautstärke) leicht verständlich. Die Pendel wirken auf den Stativstab wie die Schallwellen auf das Trommelfell. Zur genaueren Untersuchung dieses Sachverhalts denken wir uns zwei periodisch wechselnde Kräfte F1 und F2, die gemeinsam an einem Stativstab angreifen.
F1 = 1N · sin[(2 π/2) · t] ; F2 = 1N · sin[ (2 π/2,2) · t]
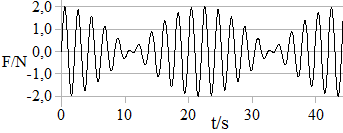
Abb. 1.8.16: Tabelle 9
Das Diagramm der Abb. 1.8.16 zeigt die Summe F = F1 + F2 der beiden Kräfte in Abhängigkeit von der Zeit. Ein Maximum tritt immer dann auf, wenn beide Schwingungen gleichsinnig sind. Wenn dies zu einem Zeitpunkt t der Fall ist, dann trifft dies wieder dann zu, wenn die Zahl der Schwingungen von F1 gegenüber der Zahl von F2 um 1 zugenommen hat.
Ist der zeitliche Abstand zweier Maxima = Ts, dann gilt demnach:
f1·Ts - f2·Ts = 1 → (f1 - f2) ·Ts = 1 → f1 - f2 = 1/Ts
f1: Frequenz von F1; f2: Frequenz von F2
Die als Schwebungsfrequenz bezeichnete Größe 1 / Ts = fs beschreibt die Zahl der in einer Zeiteinheit auftretenden Maxima. Für sie gilt: fs = f1 - f2
In dem hier beschriebenen Beispiel erhalten wir für fs:
fs = 1/(2s) - 1/(2.2 s) = 1/(22 s) → Ts = 22 s
Anmerkung zur graphischen Darstellung einer Funktion mit dem Open-Office-Tabellenkalkulationsprogramm:
In der Spalte A wird eine Tabelle mit Zeitwerten t angelegt. In der dritten Zeile wird unter A die Anweisung „= A2+$C$2“ eingetragen. $C$2 steht für ein Δt = 0,05 s. In die dritte Zeile wird unter B „= SIN($E$2*A3)+SIN((2*$E$2/$D$2)*A3)“ als Anweisung zur Berechnung des Funktionswerts geschrieben. $E$2 und $D$2 stehen für π und für die Schwingungszeit 2,2 s. Der unter A und B liegende Abschnitt der dritten Zeile wird in 2000 darunter liegende Zeilen kopiert. Anschließend wird in bekannter Weise ein x-t-Diagramm erstellt.
Wird eine von zwei einander gegenüber stehenden Stimmgabeln gleicher Frequenz angeschlagen, dann beginnt auch die zweite Gabel zu schwingen; sie empfängt einen Ton von der ersten und tönt zurück. Man spricht in diesem Fall von Resonanz (Widerhall). Die zweite Stimmgabel wird in diesem Fall von den periodisch ihre Richtung wechselnden Kräften einer Schallwelle zu Schwingungen angeregt. Das Ausmaß der Anregung ist von der Frequenz des Erregers abhängig. Vermindert man die Frequenz der ersten Stimmgabel durch Anheften eines kleinen Magneten, dann tönt nach Anschlagen dieser Gabel die zweite weit weniger stark. Abb. 1.8.7 zeigt eine Anordnung, mit der in ähnlicher Weise mit periodisch wechselnden Kräften eine Schwingung erzwungen wird. Mit ihr kann untersucht werden, wie die Amplitude der Schwingung von der Frequenz des Erregers abhängt. Ein über der Wippe aufgehängter Magnet taucht in eine auf er Wippe stehende Spule, die von einem Wechselstrom durchflossen wird, dessen Frequenz von kleinen Werten an kontinuierlich ansteigt.Der Magnet wirkt mit einer periodisch wechselnden Kraft über die Spule auf die Wippe und erregt diese zum Schwingen. Hierbei wird deutlich, dass die Schwingungsamplitude dann am größten ist, wenn die Erregerfrequenz mit der Eigenfrequenz der Wippe (10 Hz) übereinstimmt (siehe Abb. 1.8.18). In diesem Fall sagt man, die Wippe sei in Resonanz mit dem Erreger. Eine solche Resonanz wird oft als lästige Erscheinung wahrgenommen. Der Autofahrer erlebt sie manchmal als unangenehme Vibration im Fahrzeug, wenn die Reifen nicht richtig ausgewuchtet sind und infolgedessen ein Autoteil, möglicherweise das Lenkrad, dessen Eigenfrequenz der Umlauffrequenz der Reifen gleicht, zum Schwingen angeregt wird.

Abb. 1.8.17 Abb. 1.8.18
Quantitative Untersuchung einer erzwungenen Schwingung
Zur mathematischen Behandlung der erzwungenen Schwingung stellen wir uns einen Körper der Masse m vor, der an einer Feder (Federkonstante D) um den Nullpunkt eines Koordinatensystems entlang der x-Achse schwingt. Neben der Federkraft - D·x (die Federkraft ist der Auslenkung entgegen gerichtet) erfahre dieser Körper noch eine Kraft F von außen nach F = F0 ·sin(ω·t). Somit gilt: m ·a = - D · x + F0 · sin(ω·t). Wenn noch eine von der Geschwindigkeit abhängige Reibungskraft FR = - k · v zu berücksichtigen ist, dann muss die Gleichung durch - k· v ergänzt werden.
m ·a = - D · x + F0 · sin(ω·t) – k·v
In die zur Berechnung gedämpfter Schwingungen aufgestellte Tabelle wird als F1 die Kraft F1 = - D · x + F0 · sin(ω·t) – k·v eingetragen. In die dritte Zeile der Spalte A wird die Rechenanweisung „= -$K$2*I2+$O$2*SIN($P$2*H2)-$N$2*E2“ geschrieben und dann in 2000 darunter stehende Zeilen kopiert. $K$2, $O$2 und $P$2 stehen für D = 8kg/s2, F0 = 1N und ω = 6 s-1. Für die Masse m = $M$2 wird 0,2 kg eingesetzt. In Abb. 1.8.19 ist das für den reibungsfreien Fall (k = 0) erzeugte Diagramm zu sehen. Es beschreibt die nach links und rechts gehende Schwingung eines zwischen zwei nahezu waagrechten Schraubenfedern eingespannten Körpers (Eigenfrequenz fE = 1Hz), die von einer mit f = 0,95 Hz periodisch schwankenden Kraft veranlasst wird.
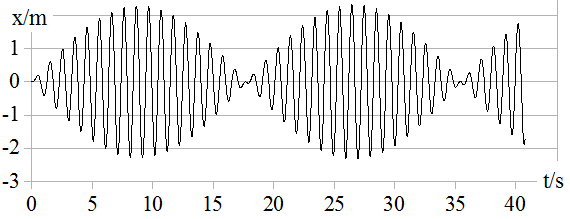
Abb. 1.8.19 Tabelle 10
Die Amplitudenschwankung werden im Hinblick auf die Abb. 1.8.20 verständlich. In dieser Abbildung ist neben dem v-t-Diagramm des schwingenden Körpers auch noch ein Diagramm zu sehen, welches die erregende Kraft F = F0 ·sin(ω·t) in Abhängigkeit von der Zeit darstellt. Zunächst hat F die Richtung von v, demzufolge wird der schwingende Körper fortwährend angetrieben und die Amplitude wächst. Ist das Amplitudenmaximum erreicht, dann hat die Kraft nur noch während zweier Viertelperioden die Richtung von v, folglich wird in gleichem Maß angetrieben wie abgebremst. Nach dem Maximum wird mehr abgebremst als angetrieben, weshalb die Amplitude abnimmt. Wenn die Geschwindigkeitsamplitude fast den Wert 0 erreicht hat, dann ist die Kraft der Geschwindigkeit während der gesamten Periodendauer entgegen gerichtet. Hiernach erfolgt eine Umkehr der Geschwindigkeitsrichtung (Phasensprung), wonach die Kraft F = F0 ·sin(ω·t) wieder mit der Bewegungsrichtung übereinstimmt und deshalb die Schwingung erneut verstärkt.
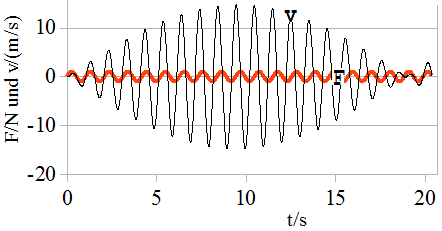
Abb. 1.8.20: v-t-Diagramm mit k = 0 ; fE = 1Hz; f = 0,95 Hz Tabelle 11
Wenn die Frequenz der Kraft gleich der Eigenfrequenz des schwingenden Körpers ist (siehe Abb. 1.8.21), dann wirkt die erregende Kraft immer in Bewegungs-richtung; die Amplitude wird bei fehlender Reibung unendlich groß .
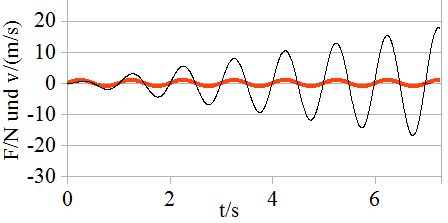
Abb. 1.8.21: v-t-Diagramm mit f = fE = 1Hz; k = 0
Das Diagramm in der Abb. 1.8.19 gleicht einem Schwebungsdiagramm, welches die Summe zweier Schwingungen anzeigt. Die eine Schwingung ist die aufgezwungene Schwingung mit der Frequenz f und die andere ist eine Eigenschwingung mit der Frequenz fE, die sich beim Anschwingen entwickelt. Wenn Reibungskräfte im Spiel sind, dann klingt die Eigenschwingung schnell ab und die Schwankungen der Amplitude unterbleiben (siehe Abb. 1.8.22).
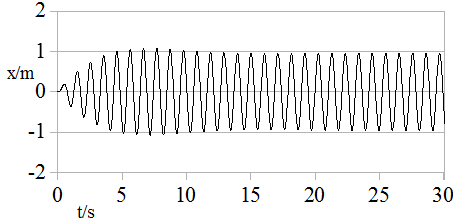
Abb. 1.8.22: x-t-Diagramm mit k = 0,1; fE = 1Hz; f = 0,95 Hz
Herleitung einer Formel für die Elongation einer erzwungenen Schwingung
Das Schwingungsdiagramm zu einer erzwungenen Schwingung ohne Reibung gleicht einem Schwebungsdiagramm, weshalb die folgende Summe für die Elongation x in Frage kommt.
x = A· sin(ω · t) + B· sin(ωE ·t)
ω = Erregerkreisfrequenz, ωE = Eigenkreisfrequenz
Die Geschwindigkeit v(0) zum Zeitpunkt t = 0 ist 0. Wie im Kapitel 1.8.1 erläutert wurde, gelten für die Geschwindigkeiten v1 und v2 der Schwingung x = A· sin(ω · t) und x = B· sin(ωE ·t):
x = A· sin(ω · t); v1 = A · ω · cos(ω ·t)
x = B· sin(ωE ·t); v2 = B·ωE· cos(ωE ·t)
↓
x = A· sin(ω · t) + B· sin(ωE ·t); v = v1 + v2 = A · ω ·cos(ω ·t) + B· ωE· cos(ωE · t)
v(0) = 0 → A · ω = - B · ωE → B = - A· ω /ωE
↓
x = A· sin(ω · t) - A· (ω /ωE) · sin(ωE ·t) → x = A· [sin(ω · t) - ω · sin(ωE ·t)/ωE]
v = v1 + v2 = A· ω · cos(ω · t) -A · ω ·cos(ωE ·t);
a = dv/dt = - A· ω2 · sin(ω · t) + A · ω ·ωE · sin(ωE ·t)
Die Gültigkeit der letzten Gleichungen kann wie folgt geprüft werden:
x =A· [sin(ω · t) - ω · sin(ωE ·t)/ωE] und die zugehörende Beschleunigung a = dv/dt werden in die Gleichung m·a = - D·x + F0 ·sin(ω·t) eingesetzt.
- m·A·ω2·sin(ω·t) + m·A·ω·ωE·sin(ωE·t) = -D·A·sin(ω·t) + D·A·ω· sin(ωE ·t)/ωE + F0·sin(ω·t)
Die fett markierten Terme heben sich wegen D = m · ωE2 auf.
- m · A· ω2 · sin(ω · t) = - D· A· sin(ω · t) + F0 ·sin(ω·t)
↓
- m · A· ω2 = - D· A + F0 → A = F0 /(D - m ·ω2) ; D/m = ωE2
↓
A = (F0/m) / (ωE2 - ω2 )
x = A·[sin(ω · t) - ω · sin(ωE ·t)/ωE] erfüllt mit A = (F0/m)/ (ωE2 - ω2 ) die Gleichung m·a = - D·x + F0 ·sin(ω·t).
Der Vorzeichenwechsel von A beim Übergang ω < ωE zu ω > ωE deutet nicht auf einen Phasensprung hin, wie dies oft fälschlicherweise sogar in manchen Lehrbüchern behauptet wird, denn mit A ändert auch die Differenz sin(ω · t) - ω · sin(ωE ·t)/ωE ihr Vorzeichen.
Wenn die Erregerfrequenz mit der Eigenfrequenz übereinstimmt (ω = ωE), dann nimmt nach Abb. 1.8.21 die Amplitude gleichmäßig mit der Zeit zu. Das muss aus x = A·[sin(ω · t) - ω · sin(ωE ·t)/ωE] hervorgehen, wenn wir ω an ωE heranrücken.
ω - ωE = Δ ω → ω = ωE + Δ ω
x = A·[sin(ωE · t + Δ ω · t) - (ωE + Δ ω) · sin(ωE ·t)/ωE]
x = A·[sin(ωE · t + Δ ω · t) - sin(ωE ·t) - Δ ω · sin(ωE ·t)/ωE]
A = (F0/m)/ (ωE2 - ω2 ) = (F0/m)/ [(ωE + ω ) ·( ωE- ω) ]= - (F0/m)/ [(ωE + ω ) · Δ ω]
x = [- (F0/m)/ (ωE + ω ) ] · {[sin(ωE · t + Δ ω · t) - sin(ωE ·t) ]/ Δ ω - sin(ωE ·t)/ωE}
x = [- (F0/m)/ (ωE + ω )] · {t·[sin(ωE · t + Δ ω · t) - sin(ωE ·t) / (Δ ω·t) - sin(ωE ·t)/ωE}
ωE · t = u, Δ ω·t = Δu
x = [- (F0/m)/ (ωE + ω )] ·{t·[sin(u+ Δ u) - sin(u) / (Δ u) - sin(ωE ·t)/ωE}
Für ω → ωE gilt : ωE + ω → 2· ωE
[sin(u+ Δ u) - sin(u)] / (Δ u) → cos u = cos ( ωE· t)
x = [- (F0/m)/ (2·ωE )] · {t· cos ( ωE· t) - sin(ωE ·t)/ωE}
↓
x = [F0/ (2·ωE · m)] · {sin(ωE ·t)/ωE - t· cos ( ωE· t)}
Ein Schüler, der mit der Differentialrechnung vertraut ist, kann mit der Regel von L'Hospital den hier gewonnenen Grenzwert ermitteln (nach ω differenzieren !) .
lim ω → ωE [sin(ω · t) - ω · sin(ωE ·t)/ωE] / (ωE2 - ω2 ) = lim ω → ωE [t · cos (ω ·t) - sin(ω ·t)/ ωE]/ (-2 ·ω )
Ist die Schwingung einer Schraubenfeder gedämpft, dann stellt sich bei einer erzwungenen Schwingung unter der Kraft F0 · sin(ω · t) ein Amplitudenmaximum ein, wenn die Erregerfrequenz f gleich der Frequenz fE = [1/(2·π)]·√(D/m) ist. fE ist die Frequenz bei fehlender Dämpfung.
Es gilt: m·a = - D·x - k·v + F0 ·sin(ω·t)
Nach dem Einschwingen kommt x = A·cos(ω·t) mit ω2 = D/m als Lösung der Gleichung in Frage.
v = -A·ω· sin(ω·t); a = -A·ω2· cos(ω·t)
-m·A·ω2· cos(ω·t) = -D·A·cos(ω·t) + k·A·ω· sin(ω·t) + F0 ·sin(ω·t)
Die fett gedruckten Terme heben sich wegen ω2 = D/m auf.
↓
k·A·ω· sin(ω·t)+ F0 ·sin(ω·t) = 0 → A = -F0 /(k· ω) → x = [-F0 /(k· ω)]·cos(ω·t)
Von einer harmonischen Schwingung spricht man, wenn die zur Ruhelage treibende Kraft F der Auslenkung x proportional ist (F = D · x , D = Konstante). Die Bewegung eines harmonisch schwingenden Körpers wird durch eine Sinusfunktion beschrieben. Bewegt sich ein schwingender Gegenstand unter einer Kraft, die einem anderen Gesetz folgt, dann hat man eine anharmonische Schwingung. Wir untersuchen nun das Verhalten eines Körpers der Masse m, der unter der Kraft F = (1-0,2·x)·x schwingt. Die Abhängigkeit der Kraft F von der Auslenkung x sehen wir in der Abb. 1.8.23. Der Betrag der zurück treibenden Kraft nimmt bei einer Bewegung nach links stärker zu als bei einer Bewegung nach rechts. Eine solche Asymmetrie der Kraft ist in der Natur häufig zu finden. Man denke z.B. an schwingende Atome an der Oberfläche eine Körpers. Schwingen diese Atome in den Körper hinein, dann erfahren sie Abstoßungskräfte von anderen Atomen. Derartige Kräfte fehlen beim Schwingen nach außen. Somit steigt die zurück treibende Kraft beim Schwingen nach außen weniger stark an als beim Schwingen in die Gegenrichtung.
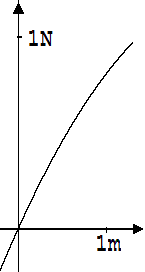
Abb. 1. 8.23
Das Diagramm in der Abb. 1. 8.24 beschreibt eine Bewegung unter der angegebenen Kraft F = (1-0,2·x)·x. An diesem Diagramm fällt auf, dass der Schwingungsmittelpunkt nach der Seite verschoben wird, von der die geringeren Gegenkräfte kommen. Diese Verschiebung nimmt mit steigender Amplitude zu. Hiermit wird die Ausdehnung von Gegenständen bei Erwärmung verständlich. Die Schwingungsmittelpunkte der nahe der Oberfläche schwingenden Atome rücken mit wachsender Amplitude (steigender Temperatur) nach außen.
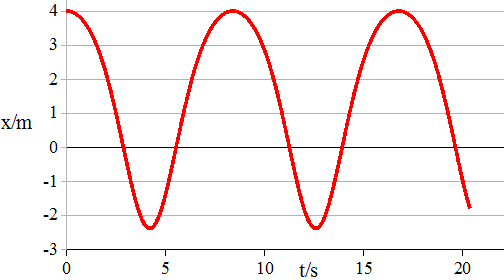
Abb. 1. 8.24 Tabelle 12
Anmerkung:
Die Elongation x jeder periodische Funktion kann, wie im Folgenden zu sehen, durch eine Summe von Sinustermen und einer Konstanten dargestellt werden. Die Methode zur Auffindung dieser Sinusterme und der zugehörenden Konstanten heißt „Fourieranalyse“ .
x = K + x01 ·sin(ω·t+α1) + x02 ·sin(2·ω·t+α2) + x03 ·sin(3·ω·t+α3) +…..
Den durch x01 ·sin(ω·t + α1) beschriebenen Anteil von x heißt Grundschwingung, die Anteile mit mehrfacher Frequenz heißen 1. , 2. , 3.Oberschwingung usw. Derartige Analysen können mit dem Programm „Mathe.-Physik“ der Firma Höhne-Messtechnik durchgeführt werden.Eine Analyse des Diagramms in der Abb. 1.8.24 ergab:
x = 1,443+3,136 * sin( 0,7396 * 1 * t + 1,609)+ 0,5879 * sin( 0,739 * 2 * t + 4,812)+ 0,071 *sin(0,739 * 3 * t + 1,720 )
Aufgaben
1. Ein U-Rohr ist in einer Länge von L = 30 cm mit Wasser gefüllt. Wird in den einen Schenkel des U-Rohrs kurzzeitig hinein geblasen, dann beginnt das Wasser zu schwingen. Wie groß ist die Schwingungszeit T ?
Abb. 1.8.25
2. Aus einer Federpistole, deren Feder die Federkonstante D = 5 N/ cm hat, wird eine 5 g schwere Kugel geschossen. In welcher Zeit t wird die Kugel auf die Geschwindigkeit beschleunigt, mit der sie die Pistole verlässt ?
3. Ein in zwei Ringen geführter Holzstab (siehe Abb. 1.8.26 ) der Länge L = 20 cm ( Dichte des Holzes ρH = 600 kg/m3) taucht in Wasser ein. Der Stab wird leicht nach unten gestoßen und beginnt dann mit kleiner Amplitude zu schwingen. Wie groß ist die Schwingungszeit T ? Die Bewegung des Wassers kann unter diesen Bedingungen außer Acht gelassen werden.
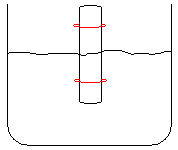
Abb. 1.8.26
4.In der folgenden Skizze sind zwei Eisenkugeln zu sehen, die mit gleich langen Fäden am gleichen Punkt aufgehängt sind. Die Kugeln lässt man aufeinander stoßen, wie dies in der Skizze angedeutet ist. Beim Zusammenstoß haften die Kugeln eine sehr kurze Zeit aneinander. Wird die Kontaktzeit größer, wenn der anfängliche Kugelabstand vergrößert wird ? Begründung der Antwort ohne Rechnung !
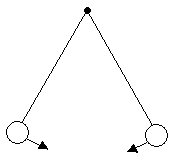
Abb. 1.8.27
5. Zur Bestimmung von g lässt man ein L = 3 m langes Pendel mit kleiner Amplitude schwingen. Mit einer Stoppuhr wird als Zeit von 40 Schwingungen 138,8 s gemessen. Welchen Wert erhält g nach diesen Daten ?
6. Eine Eisenkugel pendelt an einem 30 cm langen Faden mit kleiner Amplitude in einem mit Wasser gefüllten Becken ( Dichte ρE des Eisens = 7,86 g/cm3; Dichte ρ des Wassers = 1 g/cm3 ). Wie groß ist die Schwingungszeit ?