1.7. Bewegungen mit Reibungskräften

1.7.1 Schiefer Wurf unter Berücksichtigung der Luftreibung

Unter 1.6.3.3 wurde ein Gesetz zur Reibungskraft in Luft angegeben. Es muss berücksichtigt werden, wenn es darum geht, die Bahn einer Kanonenkugel zu bestimmen. Ein Tabellenkalkulationsprogramm macht dies möglich. Die passenden Kräfte müssen in der im Kapitel 1.4.2 aufgestellten Tabelle in den ersten beiden Spalten eingetragen werden.

Welche Kraft wirkt auf die Kugel ?

Die der Geschwindigkeit entgegen gerichtete Reibungskraft F_R ist v² proportional.

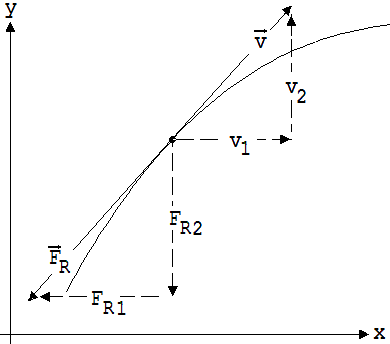
Abb. 1.7.1

F_R / v² = k; F_R = k·v² ( |v| = v ; |F_R| = F_R )

Wie die Komponenten der Reibungskraft F zu berechnen sind, erkennt man an der Abb.1.7.1. Zu sehen sind zwei ähnliche Dreiecke aus Geschwindigkeits- und Kraftvektoren.

-F_R1/ |F_R| = v₁ /|v| → F_R1 = - (v₁ /|v|) · |F_R|

- F_R2/ |F_R| = v₂ /|v| → F_R2 = - (v₂ /|v|) · |F_R|

|F_R| = k·v², v = |v| → F_R1 = - v₁ ·v · k ; F_R2 = - v₂ ·v · k

Neben der Reibungskraft wirkt noch die Gewichtskraft m·g.

F₁ = - v₁ ·v · k und F₂ = - g· m - v₂ · v · k sind die x und y- Koordinaten der auf die Kugel wirkenden Kraft.

Die im Kapitel 1.4.2 aufgestellte Tabelle kann nun zur Behandlung der Kugelbewegung hergerichtet werden. In die 1. Zeile der Spalte A schreiben wir F₁ = - v₁ ·v · k und in die 3. Zeile darunter = -E2*G2*$N$2. E2 steht für den in der zweiten Zeile unter E eingetragenen Anfangswerte von v₁ /(m/s) =15. G2 steht für die aus v₁ und v₂ gebildete anfängliche Bahngeschwindigkeit =WURZEL(E2^2+F2^2). F2 ist der Anfangswerte von v₂ /(m/s) =15 und $N$2 ist k / (kg/ m) = 0,1.

F₂ = - g· m - v₂ · v · k kommt in die 1. Zeile unter B und der entsprechende Term = -$K$2*$M$2-F2*G2*$N$2 darunter in die 3. Zeile. $K$2 und $M$2 stehen für g / (m/s²) = 9,81 und m /kg = 1 . Das Zeitintervall Δt wird als L2 eingetragen.

Anschließend werden die unter A und B liegenden Abschnitte der dritten Zeile in 2000 darunter liegende Zeilen kopiert und schließlich das in der Abb. 1.7.2 sichtbare Bewegungsdiagramm erstellt. Es ist zu sehen, dass die Bahn deutlich von einer Parabel abweicht.

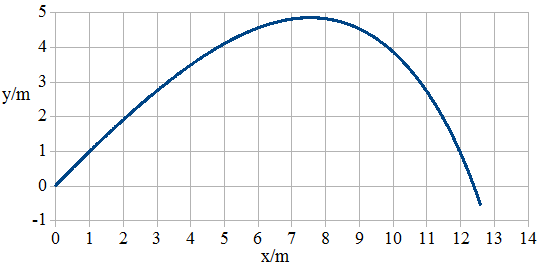
Abb. 1. 7.2 : Tabelle 4

1.7.2 Fallbewegung in einer Flüssigkeit

Wir stellen uns eine in Öl fallende Eisenkugel vor. Ihr ist ein Koordinatensystem mit einer nach unten gerichteten x-Achse zugeordnet, an deren 0-Punkt sie zum Zeitpunkt t = 0 zum Fall freigegeben wurde. Der Gewichtskraft m · g wirkt eine der Geschwindigkeit v proportionale Reibungskraft F_R = k ·v entgegen. v wächst solange bis die Gewichtskraft gleich der Reibungskraft ist.

Wie ändert sich v mit der Zeit ?

Für die Kraft F gilt: F = m· g – k · v

F₁ = m· g – k · v₁ ; F₁ = m· a₁ → a₁ = g – (k/m) · v₁

Wir tragen F₁ in die zum schiefen Wurf mit Reibung angelegte Tabelle ein. In die 3.Zeile der Spalte A schreiben wir „= $M$2*$K$2-$N$2*E2“ und kopieren diese Zeile in 2000 darunter liegende Zeilen. Als Anfangswert von v₁ wird der Wert 0 eingetragen. Für m und k werden 1 (1 kg) und 3 (3 kg/s) eingesetzt. Mit den unter H und I stehenden Zeit- und Wegwerten wird ein x-t-Diagramm (x steht für den Weg) erstellt (siehe Abb. 1.7.3).

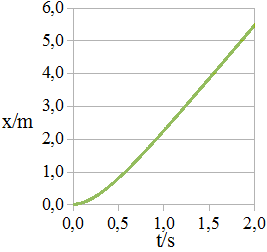
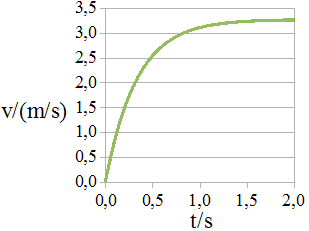
Abb. 1.7.3: Tabelle 5      Abb. 1.7.4: Tabelle 6

Zum Verständnis des Diagrammverlaufs ist ein v-t-Diagramm hilfreich. Zur seiner Darstellung wird zunächst so vorgegangen wie beim Anlegen eines x-t-Diagramms.

Zu diesem Zweck werden die Spalten G und H für ein Diagramm ausgewählt. Nach Anklicken von Diagramm- XY – Linien erscheint ein Diagramm mit einer nach oben gehenden t-Achse.

Damit diese wie in der Abb. 1.7.3 nach rechts weist, wird mit einem Rechtsklick auf dem Diagramm ein Dialogfeld mit dem Wort „Datenbereich“ aufgerufen. Nach Wahl von „Datenbereiche“ werden in „Datenreihen“ die Buchstaben G und H vertauscht. Das v-t-Diagramm zeigt eine Höchstgeschwindigkeit unter der folgender Bedingung an:

a₁ = m · g - k ·v_max = 0 ↔ v_max = m · g/k .

Die Annäherung der Geschwindigkeit an ihren Endwert ähnelt der Massenabnahme während des in der Abb. 1.6.15 skizzierten Experiments.

Vermutlich gilt: ( v_max – v) = m·g / k – v = (m·g / k)·e ^{- c· t} → v = m·g / k · (1- e ^{- c· t} )

Wir prüfen diese Gleichung mit dem noch unbekannten Faktor c auf seine Gültigkeit, indem wir die ihr entsprechende Geschwindigkeit v und Beschleunigung a₁ = dv/dt in a₁ = F₁ / m = g – (k / m) · v einsetzen.

Zur Ermittlung von dv/dt wird die unter 1.6.3.2 angegebene Regel zur Ableitung von f(t) =A·e^b·t angewandt.

a₁ = m·g/k · (- c ) · e ^{- c· t}, v = m·g/k · (1- e ^{- c· t} )

a₁ = g – (k / m) · v → m·g / k · (-c) · e ^{- c· t} = g – (k / m)· m·g / k · (1- e ^{- c· t} )

(- c) · e ^{- c· t} = k / m – (k / m) · (1- e ^{- c· t} ) → - c · e ^{- c· t} = - (k / m) · e ^{- c· t}

Mit c = k / m erfüllt v = m·g / k · (1- e ^{- c· t} ) die Gleichung a₁ = g – (k / m) · v.

Für den Ort x der Kugel zum Zeitpunkt t kommt eine Funktion in Frage, die m·g/k · (1- e ^{- (k/m)· t} ) als Ableitung hat.

Die Funktion „x = (m·g/k) ·(t + m/k· e ^{- (k/m) · t}) + Konstante“ hat diese Eigenschaft.

Beweis: dx/dt = (m·g / k) (1 + (m / k) · (- k / m) · e ^{- ( k / m ) · t} ) = m·g / k · (1- e ^{- ( k / m ) · t} )

Die Konstante muss so bestimmt werden, dass x im Fall t = 0 den Wert 0 hat.

x_(t=0) = (m·g / k) (0 + m / k ) + Konstante = 0 → Konstante = - m² ·g / k²

x = ( m · g / k ) ·( t + m / k · e ^{- (k / m) · t} ) - m² · g / k² →     x = (m·g/k) ·t - (m²·g/k² ) · (1- e^{- (k /m)· t})