1.5 Gesetze zur Kraft
1.5.1 Das Wechselwirkungsgesetz
1.5.1.1 Kräfte beim Anfahren und Bremsen eines Autos
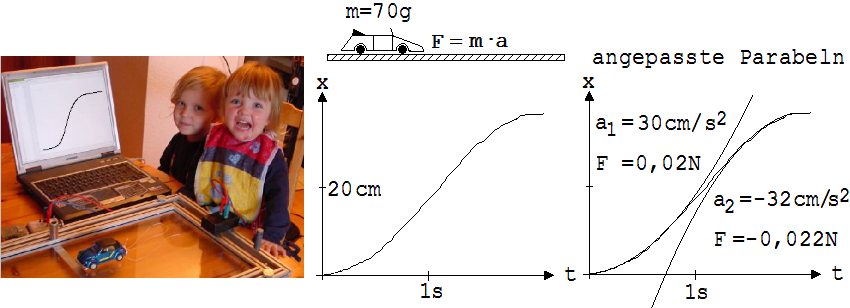
Ein Spielauto mit leicht aufgezogenem Federmotor wird zunächst am Rand der Wippe mit einem Faden festgehalten und in einem passenden Augenblick freigegeben (siehe Abb. 1.5.1 und Abb. 1.5.2).

Abb. 1.5.1 Abb. 1.5.2
Der Anfang und das Ende des hierbei aufgezeichneten s-t-Diagramms ist durch parabelförmige Abschnitte gekennzeichnet, die eine gleichförmig beschleunigte Bewegung mit positiver bzw. negativer Beschleunigung anzeigen. Wenn die Geschwindigkeit v in Richtung der x-Achse größer wird (Δv > 0), dann spricht man von einer positiven, andernfalls von einer negativen Beschleunigung. Mit Computerprogrammen (Mathe.-Physik, CASSY-LAB) können dem Bewegungsdiagramm Parabeln angepasst und die zugehörenden Terme bestimmt werden. Der Faktor vor t2 gleicht der halben Beschleunigung. Nach Kenntnis der Beschleunigung ist die Berechnung der Kraft während des Anfahrens und Bremsens möglich.
Wer beschleunigt das Auto ? Warum fährt ein Auto an ?
Der Motor kann nicht als unmittelbare Ursache angesehen werden, da nach dem Trägheitssatz nur äußere Kräfte eine Beschleunigung herbeiführen. Die Kraft muss von der Straße ausgehen. Die Räder greifen an der Straße an und verformen deren Oberfläche so, dass die Straße wie eine gestauchte Feder auf das Auto einwirkt.
Zur Überprüfung dieses Sachverhalts denken wir uns ein Spielauto auf einer beweglichen Fahrbahn (siehe Abb.1.5.3).

Abb. 1.5.3: 2 Experimentierwagen tragen eine Glasplatte
Fährt das Spielauto an, dann erfahren sowohl das Auto wie die bewegliche Fahrbahn einen Impuls. Nach dem Impulssatz müssen die beiden Impulse betragsmäßig übereinstimmen. Das Auto übt dementsprechend eine Kraft auf die bewegliche Fahrbahn aus (erteilt ihr einen Impuls entgegen der eigenen Bewegungsrichtung ), und diese wirkt mit einer gleich großen Kraft auf das Auto.
Wir schließen hieraus auf das Wechselwirkungsgesetz:
Jeder Kraft wirkt eine gleichgroße Kraft entgegen.
Immer wieder weisen alltägliche Erfahrungen auf das Wechselwirkungsgesetz hin.

Abb. 1.5.4 Abb.1.5.5
In der Abb. 1.5.4 sind Kinder auf einem Floß zu sehen. Sie ziehen an einem Seil, welches die beiden Ufer eines Flüsschens miteinander verbindet und erzeugen damit eine Gegenkraft des Seils, die ihre Bewegung veranlasst.
Die nach dem Wechselwirkungsgesetz zu erwartende Gegenkraft ist häufig Ausdruck einer Verformung. Selbst die Wand eines Klassenzimmers wird unter dem Druck einer Hand verbogen. Eine solche Wandverbiegung kann mit der Experimentierwippe nachgewiesen werden ( siehe Abb. 1. 5.5).
Zwischen dem Stativstab auf dem Rand der drehbaren Glasplatte und einer Wand (keine Betonwand) wird ein dünner Stahldraht straff aufgespannt. Eine durch Händedruck verursachte Verformung der Wand bewirkt eine geringe Drehung der Glasplatte, die in bekannter Weise von einem Rechner registriert wird.
1.5.2 Gesetz zur Addition der Kräfte
Wir stellen uns eine Glasplatte der Masse m3 vor, die auf kleinen Eisenkugeln aufliegt und somit nach allen Seiten frei beweglich ist.Auf der zunächst ruhenden Platte fährt ein Spielauto W1 mit der Masse m1 und dann in einem zweiten Versuch ein Spielauto W2 mit der Masse m2 an. Nach dem Impulssatz bleibt die Impulssumme aus den Impulsen des Glasplattenschwerpunkts und des Autos in jedem Fall konstant.

Abb. 1.5.6
Nach dem Impulssatz bleibt die Impulssumme aus den Impulsen des Glasplattenschwerpunkts und des Autos in jedem Fall konstant.
Deshalb gilt beim ersten Experiment:
d(m3· v3)/dt + d(m1· v1)/dt = 0 → d(m3· v3 )/dt = - d(m1· v1)/dt
v3: Geschwindigkeit des Schwerpunkts
und beim zweiten Experiment:
d(m3· v3)/dt + d(m2· v2)/dt = 0 → d(m3· v3)/dt = - d(m2· v2)/dt.
Wir denken uns die Platte gedanklich in viele kleine Teilchen zerlegt. Die Summe der Teilchenimpulse ist der Impuls m3· v3 des Schwerpunkts.
- d(m1· v1)/dt und - d(m2· v2)/dt sind die Kräfte F1 und F2 , welche die Autos W1 und W2 jeweils auf die Glasplatte ausüben.
Wenn W1 und W2 gleichzeitig anfahren, dann gilt: d(m3 · v3)/dt + d(m1 · v1)/dt + d(m2 · v2)/dt = 0
- d(m1 · v1)/dt - d(m2 · v2)/dt = d(m3 · v3)/dt
Der Schwerpunkt der Glasplatte verhält sich so, als ob nur die Kraft F3 = d(m3 · v3)/dt auf ihn wirke.
Diese Kraft erhalten wir durch vektorielle Addition der von W1 und W2 ausgehenden Kräfte F1 und F2.
Schlussfolgerung: Wirken auf einen Körper K (hier eine Glasplatte) zwei Kräfte F1 und F2 , dann verhält sich der Schwerpunkt von K so, als ob nur eine der Vektorsumme F1 + F2 gleichende Kraft F3 auf ihn einwirke.
a = F3 / (Masse von K) ist die Beschleunigung des Körperschwerpunkts.
Nach F = m·a wird die Schwerpunktbeschleunigung a eines Systems berechnet. Hierbei ist es ohne Bedeutung, ob zwischen den Teilen des Systems feste oder keine Bindungen bestehen. m steht für die gesamte Masse des Systems und F für die Vektorsumme aller auf das System wirkenden Kräfte.
Berechnung von resultierenden Kräften
An einem Gegenstand greifen zwei Kräfte F1 und F2 an. Der Winkel zwischen den Kraftpfeilen sei α (siehe Abb. 1.5.7). Wie groß ist der Betrag der resultierenden Kraft F ?

Abb. 1.5.7
Zur Beantwortung einer solchen Frage wird ein Dreieck aus den Kraftvektoren gebildet. F erscheint als unbekannte Seite in dem aus F1, F2 und F gebildeten Dreiecks. Für den Gegenwinkel γ zu F gilt: γ = 180° - α . |F | ist mit Hilfe des Kosinussatzes berechenbar.
|F|2 = |F1|2 + |F2|2 – 2· |F1| ·|F2|·cos γ
Anwendungen des Additionsgesetzes
Die Hangabtriebskraft
Behauptung: Ein Wagen, der auf einer schiefen Ebene die Höhendifferenz s durchläuft, erfährt eine nur von s abhängige Geschwindigkeitsänderung.
Beweis:
Die Beschleunigung eines Wagens der Masse m entlang der schiefen Ebene weist auf eine Kraft F (Hangabtriebskraft) parallel zu dieser Ebene hin; sie ist die Resultierende der auf den Wagen wirkenden Kräfte. Auf den Wagen wirkt die Erde mit ihrer Anziehungskraft FG = m·g und die schiefe Ebene mit einer Abstoßungskraft FB (siehe Abb.1.5.8). Von Reibungskräften soll abgesehen werden.

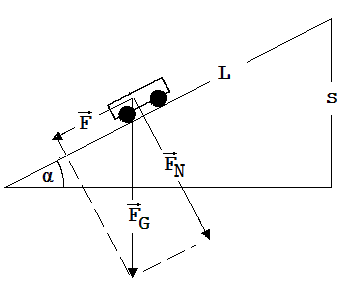
Abb.1.5.8 Abb.1.5.9
F/FG = s/L → F = (s/L) · m · g = m · a → a = (s/L)·g
↓
(v2 – v1)/t = (s/L)·g
v1: Anfangsgeschwindigkeit; v2: Endgeschwindigkeit; t: Bewegungszeit
(v2 – v1)/t = (s/L)· g → (v2 – v1) · L / t = s· g
Für die mittlere Geschwindigkeit L/t gilt: L/t = (v2 + v1)/2
(v2 – v1) · L/t = s· g → (v2 – v1) · (v2 +v1) / 2 = s· g → v22 – v12 = 2· s· g
Demnach ist die Änderung von v2 und somit auch die von v nur von der Höhenabnahme s abhängig.
Die Hangabtriebskraft F gewinnt man auch, indem man die Gewichtskraft FG wie in der Abb. 1.5.9 sichtbar in zwei Kräfte F und FN (Normalkraft) zerlegt. Erlaubt ist dies, weil nach dem Additionsgesetz der Kräfte F und FN zusammen die gleiche Wirkung auf den Wagen haben wie FG alleine.
Die anfangs stehende Behauptung über die Änderung der Geschwindigkeit gilt auch dann, wenn der Wagen eine gekrümmte Bahn hinab rollt. In diesem Fall können wir die Bahn als eine Folge von n vielen kleinen schiefen Ebenen mit der Höhendifferenz Δs sehen (siehe Abb. 1. 5.10). Für jede dieser kleinen Ebenen gilt:
vEnde2 – vAnfang2 = 2· Δs· g

Abb. 1.5.10
Für die Summe aller n Differenzen vEnde2 – vAnfang2 erhalten wir:
v22 – v12 + v32 – v22 + v42 – v32 ….+ vn2 – vn-12 = 2· Δs1 ·g + 2· Δs2· g + 2· Δs3· g.....
Auf der linken Seite heben sich vn-12, vn-22 ….... v22 gegenseitig auf.
vn2 – v12 = 2· g ·( Δs1 + Δs2 + Δs3 …...) = 2· g ·s
Experimentelle Überprüfung der letzten Aussage

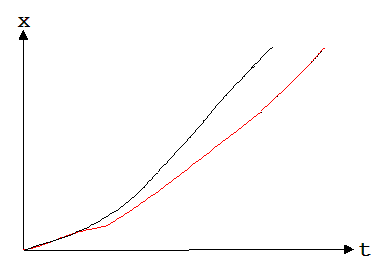
Abb. 1.5.11 Abb. 1.5.12 Abb. 1.5.13
Die Abb. 1.5.11 und 1.5.12 zeigen eine in Querrichtung geneigte Wippe (die Schmalseiten sind geneigt, die Längsseiten verlaufen waagrecht), auf der eine Kugel entlang einer vorgeschriebenen Bahn hinab rollt. Die Bahn ist jeweils durch einen Schweißdraht (Durchmesser = 4 mm) vorgegeben, der zwischen zwei diagonal gegenüber liegenden Ecken der Wippe eingespannt ist. Die in den Abbildungen erkennbaren Bahnen nehmen vor dem unteren Ende einen waagrechten Verlauf an, somit werden die mit der Geschwindigkeit 0 am oberen linken Ende der Bahn beginnende Bewegungen am Ende gleichförmig. In der Abb. 1.5.13 sind die zugehörenden Weg-Zeit-Diagramme zu sehen ( das obere ist der Abb. 1.5.11 und das untere der Abb. 1.5.12 zuzuordnen). Beide Diagramme haben am Ende gleiche Steigungen und zeigen somit gleiche Endgeschwindigkeiten an.
Kräfte an einer tragenden Leine
An einer Leine, die zwischen zwei Punkten P1 und P2 aufgespannt ist, sei eine Lampe aufgehängt (siehe Abb. 1.5.14). Man könnte meinen, dass P1 und P2 jeweils die halbe Gewichtskraft der Lampe aushalten müssen. Dies ist aber nicht der Fall. Die auf sie wirkenden Zugkräfte sind meistens erheblich größer als die halbe Gewichtskraft des aufgehängten Gegenstandes.
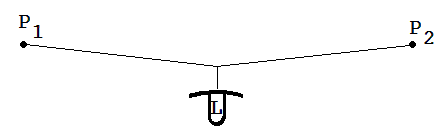
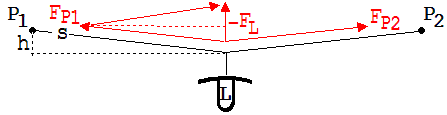
Abb. 1.5.14 Abb. 1.5.15
Warum ist dies so ?
Zum Verständnis dieses Sachverhalts dient die Abb. 1.5.15. Die von den Punkten P1 und P2 ausgehenden Kräfte FP1 und FP2 bilden als Resultierende die Gegenkraft –FL zur Gewichtskraft FL der Lampe.
Die Kräfte FP1 und FP2 ( |FP1| = |FP2|) sind größer als FL /2.
Es gilt: |FP1| / (|FL| /2) = s/h → |FP1| = (s / h) · (|FL|/2)
s: halbe Seillänge, h: Verschiebung der Seilmitte unter der Gewichtskraft der Lampe
Nach dem Wechselwirkungsgesetz haben die auf P1 und P2 wirkenden Kräfte die gleichen Beträge wie die von P1 und P2 ausgehenden Kräfte. Die Zugkraft der Lampe an einer Seilhälfte ist demnach um den Faktor s/h größer als die halbe Gewichtskraft |FL|/2 der Lampe.
Aufgaben
1. Ein Faden, an dessen Enden Gewichte mit m1 = 200 g und m2 = 160 g hängen, ist über eine feste Rolle gelegt. Wenn das 200g-Gewicht G freigegeben wird, dann bewegt es sich mit einer Beschleunigung a abwärts.
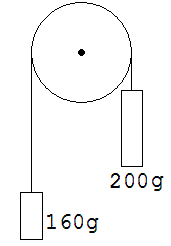
Abb. 1.5.16
Wie groß ist diese Beschleunigung a ? Welche Geschwindigkeit v hat das 200g-Gewicht 0,5 s nach seiner Freigabe ? Welchen Weg legt G in 0,5 s nach dem Start zurück ? Wie groß ist die Zugkraft F des Fadens ? Wie groß ist die Kraft auf die Rolle ?
Die Masse der Rolle sowie die Reibung der Rolle an ihrer Drehachse sei vernachlässigbar klein.
Auf einer waagrechten- und einer schiefen Ebene stehen die Wagen W1 und W2. W2 zieht W1 an einem Faden. Die Masse der Rolle R sei vernachlässigbar klein. Wie groß ist die Beschleunigung der beiden Wagen ? Wie groß ist die Kraft F auf die Umlenkrolle R ?
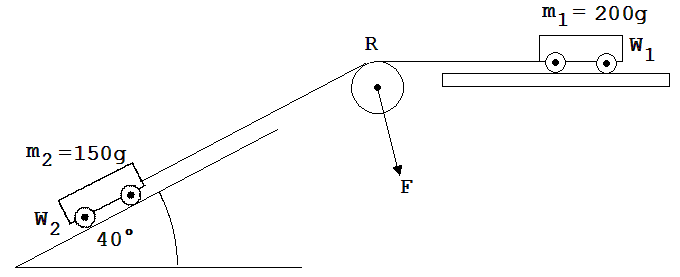
Abb. 1.5.17
3. An einem Flaschenzug hängen zwei Gewichte der Masse m =100 g. Welche Beschleunigung a1 erfährt das linke Gewicht nach seiner Freigabe ? Die Massen der Rollen sind zu vernachlässigen ! Beachte: Die Zugkräfte Ff der 3 Seilstücke sind gleich groß !
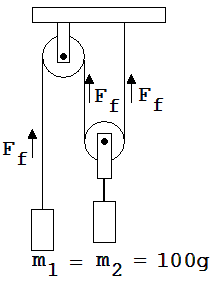
Abb. 1.5.18
4. Beweise den Galileischen Sehnensatz !
In seinem berühmten Werk „Discorsi“ behauptet Galilei Folgendes: Wenn von dem höchsten Punkt oder von dem Gipfel eines (vertikalen) Kreises (siehe Abb. 1.5.19) nach dem Horizonte hin geneigte Ebenen bis zu der Kreisperipherie errichtet werden, so sind die Fallzeiten längs derselben einander gleich (Physikaufgaben von Dr. K. Petanides, Klett-Verlag).
Nach dieser Behauptung unterscheiden sich die Zeiten t1 und t2 nicht, während der die beiden durchlochten Perlen P1 und P2 entlang gespannter Drähte von A aus reibungsfrei zum Ende des Drahtes abwärts gleiten.
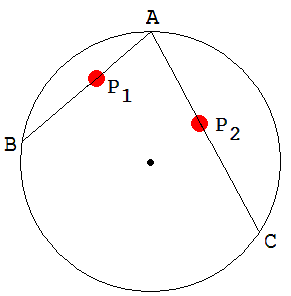
Abb. 1.5.19