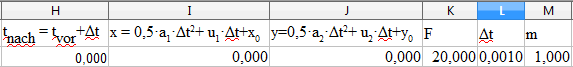1.4
Bewegung unter einer Kraft mit konstantem Betrag
1.4.1
Geradlinige Bewegung
Es
gibt eine Vielzahl von Bewegungen, die unter konstanter Kraft
ablaufen. Man denke zum Beispiel an einen Wagen auf einer schiefen
Ebene, an das Abbremsen eines Autos oder den Wurf eines Körpers.
Bei der Behandlung solcher Bewegungsarten beschränken wir uns
zunächst auf die geradlinige Bewegung.
-
|
Man
stelle sich einen Körper K der Masse m vor, der unter
einer Kraft F entlang der x-Achse bewegt wird (siehe Abb.
1.4.1). Zum Zeitpunkt t = 0 befinde er sich am Ort x0
und habe die Anfangsgeschwindigkeit v1,0.
Kräfte,
Beschleunigungen und Geschwindigkeiten in x-Richtung
erhalten den Zeiger (Index) 1!
|
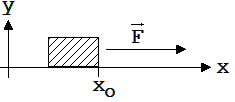
Abb.
1.4.1
|
Welche
Geschwindigkeit v1
hat
der Körper zu einem späteren Zeitpunkt t ?
Es
gilt: F1
=
m · a1
→ a1
=
F1
/m
Da
die Beschleunigung konstant ist, gehören zu gleichen Zeiten
gleiche Geschwindigkeitsänderungen. Die Änderung der
Geschwindigkeit v1 – v1;0 ist der Zeit t
proportional.
(v1
– v1,0
)/t = a1
→ v1
= a1
·t + v1,0
Welchen
x-Wert hat der Körper zum Zeitpunkt t ?
Bei
konstanter Beschleunigung ist die mittlere Geschwindigkeit gleich dem
Mittelwert aus Anfangs- und Endgeschwindigkeit.
(x
- x0)/t
= (v1
+ v1,0
)/2
v1
= a1
· t
+ v1,0
↓
(x-x0)/t
= [( a1 ·t
+ v1,0)+
v1,0 ]/2
= ½
· a1
·t + v1,0
→ x
= ½ ·
a1 ·t²
+ v1,0 ·t
+ x0
Bei
einer räumlichen Bewegung von K erhält man für dessen
Projektionen P1,
P2,
und P3
auf
die Achsen des Koordinatensystems:
|
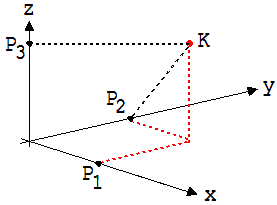
Abb.
1.4.2
|
v1
=
a1·t
+ v1,0
;
x
= ½
·
a1
·
t2
+
v1,0
·
t + x0
v2
=
a2·t
+ v2,0
;
y
= ½
·
a2
·
t2
+
v2,0
·
t + y
v3
=
a3·t
+ v3,0
;
z
= ½
·
a3
·
t2
+
v3,0
·
t + z0
v1,0
,
v2,0
,v3,0:
Geschwindigkeiten zum Zeitpunkt t = 0
x0,
y0, z0: Koordinaten
von K zum Zeitpunkt t = 0.
|
Die
Beschleunigungen können bei konstanter Masse aus den
Kraftkoordinaten F1 = m· a1 ; F2
= m· a2; F3 = m·
a3 bestimmt werden. Die zuletzt angegebenen Gleichungen
werden zu Vektorgleichungen zusammengefasst.
{v1
; v2 ; v3 } = {a1 ; a2 ;
a3 }· t + {v1,0 ; v2,0 ; v3,0
}
v
= a·t + v0
{x;
y; z } = ½ ·
{a1 ;
a2 ;
a3 }·
t2 +
{v1,0 ;
v2,0 ;
v3,0 }
·t + {x0
; y0;
z0 }
r
= ½ ·a·t2
+ v0 ·
t + r0
r
= {x; y; z }; v0
= {v1,0
; v2,0
; v3,0
}; r0
= {x0;
y0;
z0 }
Wirkt
keine Kraft ( a = 0),
dann verläuft die Bewegung gleichförmig nach
r
= v0·t
+ r0 .
K
weicht zum Zeitpunkt t um ½
·a·t2
von
dem Ort P’ ab, den K bei fehlender Kraft genau dann erreicht
hätte und hat in Bezug auf diesen Ort die Geschwindigkeit a·t.
Der
Wurf als Beispiel
Für
die Bewegung unter einer konstanten Kraft F
gelten
die folgenden Gleichungen: v
=
a·t
+
v0;
r
=
½
·a·t2
+
v0
·
t + r0;
a
=
F/m
v0:
Vektor der Anfangsgeschwindigkeit; r0: Ortsvektor
der Startpunktes
Wir
gehen davon aus, dass die Erdanziehungskraft auf einen hoch
geworfenen Körper K eine konstante, nach unten gerichtete Kraft
F ist und dass ihr demnach ein konstanter, nach unten gerichteter
Beschleunigungsvektor a zugeordnet werden kann. In einem
Koordinatensystem ( siehe Abb. 1. 4.3) mit einer nach oben
gerichteten y-Achse ist a = {0, -g, 0 }. g ist der Betrag der
Erdbeschleunigung, der in Mitteleuropa 9,81 m/s2
beträgt.
|
Das
nebenstehende Koordinatensystem zur Beschreibung des Wurfs ist
ein sogenanntes Rechtssystem. Die x-, die y- und die z-Achse
verhalten sich ihrer Richtung nach wie der Daumen, der Zeige- und
der Mittelfinger der rechten Hand, wenn der Mittelfinger von den
beiden anderen rechtwinklig abgespreizt ist.
|
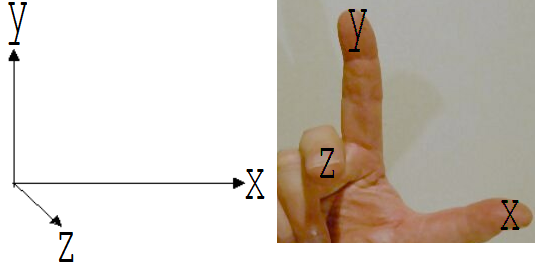
Abb.
1.4.3
|
Liegen
r0
und v0
in der x-y-Ebene dann gilt:
{x;
y; z } = ½ · {0; -g, 0} · t2
+ {v0,1;
v0,2;
0 } · t + {x0
; y0
; 0 }
{v1;
v2;
0 } = {0; -g, 0} · t + {v0,1;
v0,2;
0 }
In
diesem Fall können die z-Koordinaten unbeachtet bleiben. Für
die anderen Koordinaten gilt:
x
= v0,1·
t + x0;
y
=
-
½ · g · t2
+ v0,2
· t + y0
v1
=
v0,1
;
v2
=
-g
· t + v0,2
Bei
fehlender äußerer Kraft würde sich K nach {x; y } =
{v0,1;
v0,2
}· t + {x0
; y0
} bewegen (a = 0) und in der Zeit t mit konstanter Geschwindigkeit
einen Punkt P’ erreichen. Stattdessen gelangt K in dieser Zeit
zu einem Punkt, der g
· t2 /2 unter P’ liegt (siehe Abb. 1.4.4 ).
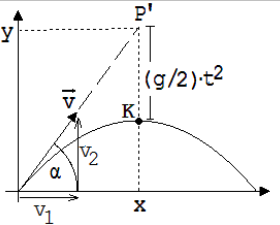
1.4.4
Die
oben angegebenen Gesetze passen auch zu einer Kugel K, die über
eine schiefe Ebene rollt. Die x und y-Achsen müssen in diesem
Fall in der schiefen Ebene liegen und zwar so, dass die x-Achse
waagrecht und die y-Achse schräg nach oben weist. Zur Berechnung
ist anstelle von g die Beschleunigung einer abwärts rollenden
Kugel einzutragen. Die Projektion der Kugel auf der x -Achse bewegt
sich gleichförmig, die Projektion auf die y-Achse
gleichförmig-beschleunigt. Die letzten Aussagen sind leicht mit
der Experimentierwippe nachprüfbar. In der Abb. 1. 4.5 auf der
sind Bewegungen auf einer schräg geneigten Wippe dargestellt. P
ist die Projektion der rollenden Kugel K auf die Längskante der
Glasplatte.
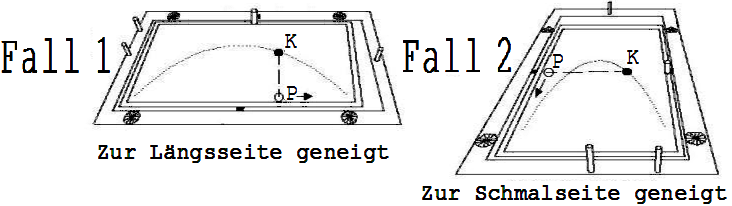
Abb.
1.4.5
Die
von dem an die Wippe angeschlossenen Rechner geschriebenen
Weg-Zeit-Diagramme sind dem Punkt P zuzuordnen.
Die
Diagramme zeigen: P
bewegt sich im Fall 1 erwartungsgemäß gleichförmig
und im Fall 2 mit einer konstanten Beschleunigung, die unabhängig
ist von der Bewegung in horizontaler Richtung.
Anmerkung
für den Experimentator: Beide Rändelschrauben der
angehobenen Längsseite sind unterlegt
Das
in Abb. 1.4.6 dargestellte Experiment dient zur Prüfung der für
einen Wurf aufgestellten Bewegungsgleichungen.
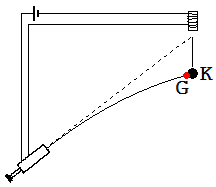
Abb.
1.4.6
Mit
einer Federkanone (siehe Abb. 1.4.6) wird eine an einem
Elektromagneten hängende Eisenkugel K anvisiert. Mit dem Schuss
wird der Strom durch den Magneten unterbrochen und die Kugel fällt.
Das Geschoss G, welches den Lauf der Kanone verlässt, trifft die
Kugel.
Erklärung:
Bei
fehlender Erdanziehungskraft würde das Geschoss G zu einem
Zeitpunkt t (Wurfbeginn bei t = 0) den Magneten erreichen. Unter der
Kraft m· g ist das Geschoss ½ ·
g ·t2 tiefer und somit am Ort der fallenden
Kugel.
Die
Gewichtskraft ist nach Richtung und Betrag konstant, sie ist
unabhängig vom Verlauf der Bewegung. Dies ist die Voraussetzung
für die Herleitung der Bewegungsgleichungen, die mit den gerade
beschriebenen Experimenten auf ihre Richtigkeit geprüft wurden.
Aufgabe:
Ein Gegenstand K werde mit der Geschwindigkeit v unter dem
Höhenwinkel α am Ort P(0;0) nach oben geworfen (siehe Abb.
1.4.4 ). Welchen Ort P(x; y) erreicht dieser Gegenstand in einer Zeit
t nach dem Abwurf ?
v1
/v =
cos(α) → v1
= v·cos(α),
v2
/v =
sin(α) → v2
= v · sin(α)
x
= t · v · cos(α) , y = t· v ·
sin(α) - (g/2) · t2
x
= t·v · cos(α) , y = t· v·sin(α)
sind die Koordinaten des Punktes P’, den K ohne Erdanziehung (
g = 0) in der Zeit t erreichen würde. Die Gleichung x = t·v
·cos(α) kann man nach t auflösen und erhält t
= x / [v · cos(α)]. Ersetzt man in der für y
gültigen Gleichung die Zeit t durch diesen Term, dann erhält
man eine quadratische Funktion, die durch eine Parabel dargestellt
wird.
y
= x · (sin α / cos α ) - g · x2
/ (2 · v2 · cos2 α )

Abb.
1.4.7
Auch
eine Wurfbahn !
Aufgaben
|
1.
Ein 200 g schwerer Wagen steht auf einer waagrechten Ebene. Vom
Wagen geht ein Faden aus, er läuft über eine Rolle
abwärts und trägt am anderen Ende ein 20g-Gewicht.
|
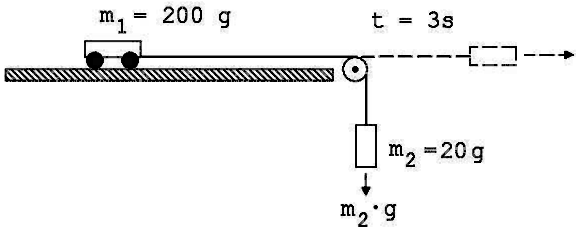
Abb.
1.4.8
|
Welche Geschwindigkeit hat der
anfänglich ruhende Wagen 3s nach seiner Freigabe ? Welchen
Weg legt er innerhalb von diesen 3 s zurück ?
Wir
gehen davon aus, dass es ohne Bedeutung für die Bewegung des
Wagens ist, ob die auf m2
wirkende
Kraft F = m2·
g nach unten oder nach rechts gerichtet ist.
2.
Ein Gegenstand wird mit v0 = 10 m/s senkrecht nach oben
geworfen.
Welche
Höhe erreicht er und wie lange dauert der Wurf ?
3.
Ein
Gegenstand wird mit v0 =
-5 m/ s von einem y0 =
10 m hohen Turm senkrecht nach unten geworfen.
Wie
lange dauert der Wurf und mit welcher Geschwindigkeit schlägt
der Gegenstand auf den Boden ?
4.
Ein Ball wird mit 15 m/s unter dem Höhenwinkel 45° aus 1,7 m
Höhe nach oben geworfen.
Welche
Höhe erreicht der Ball, wie weit fliegt er, mit welcher
Geschwindigkeit und unter welchem Winkel schlägt der Ball auf
den Boden ?
1.4.2 Bewegung auf einer
Kreisbahn
Wenn
eine Kraft auf einen Körper K wirkt, erwartet man an K eine
Veränderung des Geschwindigkeitsbetrages. Dies ist nicht immer
der Fall, z.B. dann nicht, wenn es sich um eine Normalkraft handelt,
wenn die Bewegungsrichtung mit der Richtung der Kraft einen rechten
Winkel bildet. Man denke an einen Körper der Masse m, der an
einem Faden auf einer Kreisbahn geführt wird. Wir untersuchen
nun eine Bewegung in der x-y-Ebene unter einer dem Betrage nach
konstanten Normalkraft F = {F1 ; F2 ;
0}.
In
der Schule ist die mathematische Behandlung dieser Bewegung nur mit
Hilfe eines Rechners möglich. Hierbei wird in folgender Weise
vorgegangen: Die Bewegungszeit wird in sehr kleine Zeitabschnitte Δt
zerlegt. Ein Δt ist so klein, dass innerhalb dieses Abschnitts
die Kraft nach Richtung und Betrag als konstant angesehen werden
kann. Mit den für konstante Kräfte geltenden
Bewegungsgleichungen wird die Orts- und Geschwindigkeitsänderung
während des ersten Zeitabschnitts Δt berechnet.
a1
=
F1/m,
a2 = F2/m
F1, F2 :
Kraftkomponenten in x- und y-Richtung während des Zeitabschnitts
Δt
a1, a2:
Beschleunigungen in x- und y-Richtung
v1 = a1·
Δt + u1
, v2 = a2·
Δt + u2
u1,u2 :
Geschwindigkeiten vor Δt
, v1, v2 :
Geschwindigkeiten nach Δt
x = 0,5 · a1 ·
Δt2 + u1
· Δt + x0
, y
= 0,5 · a2 · Δt2
+ u2 · Δt
+ y0
x0, y0 :
Koordinaten vor Δt
, x, y :
Ortskoordinaten nach Δt
Nach dieser Rechnung ist der Ort
und die Geschwindigkeit zu Beginn des zweiten Abschnitts Δt
bekannt. Mit diesen Werten wird daraufhin der Ort und die
Geschwindigkeit zu Beginn des dritten Abschnitts ( nach dem Ende des
2. Abschnitts) berechnet usw..
|
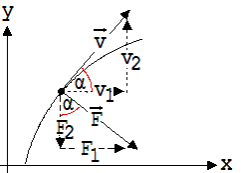
Abb. 1. 4.9
|
Die Koordinaten F1
und F2 der dem Betrage nach konstanten Kraft F
(|F| = F) werden wie folgt bestimmt:
F1 / |F| = v2
/ |v| , - F2 / |F| =
v1 / |v|
|F| = F , |v| =
v, v = √(v12
+ v22)
↓
F1
=
(v2
/v)·
F, F2
=
-(v1
/v)·
F
|
Manchmal
ist auch eine Angabe über die Bewegungszeit gewünscht. Hat
diese vor Δt den
Wert tvor
,
dann ist sie nach Δt gleich
tnach
=
tvor
+Δt.
Die
im Microsoft-Office und Open-Office (Sun) enthaltenen
Tabellenkalkulationsprogramme eignen sich zur Ausführung der
hier angegeben Berechnungsschritte.
Diese
Tabellenkalkulationsprogramme zeigen viele Spalten an, die mit
A,B,C.. überschrieben sind. Wird in der n. Zeile unter einem
Buchstaben z.B. A eine Zahl oder ein Text eingetragen, dann werden
diesem Eintrag die Variablen An und $A$n zugeordnet. Wird in ein
anderes Feld „=An“ z.B. „=A5“ eingetragen,
dann erscheint der zugehörende Eintrag nach dem Anschlag der
Taste „Zeilenwechsel“ auch in der andern Zeile. „=$A$n“
und „=An“ stehen für das Gleiche. Was sie
unterscheidet, wird der Leser bald erkennen.

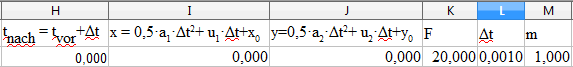
Abb. 1.4.10
Wie
ist nun bei der hier vorliegenden Augabe vorzugehen? Es
wird eine Tabelle erstellt, wie sie unter www.g-hoehne.de/T/T1.ods
heruntergeladen
werden kann. Zuallererst
werden in die erste Zeile die gerade aufgestellten Gleichungen
eingetragen. In die zweite Zeile werden die Anfangswerte von x , y,
v1,
v2
sowie die konstanten Werte F / Newton = 20, Δt
/ Sekunde = 0,001 und Masse / kg = 1 geschrieben. Die Gleichungen in
der ersten Zeile werden vom Rechner nicht als Rechenanweisungen
erkannt. Entsprechende, dem Rechner verständliche
Rechenanweisungen (siehe folgende Tabelle) werden darunter in die
dritte Zeile geschrieben.
Mit ihnen werden die Geschwindigkeiten und Ortskoordinaten am Ende
der ersten Zeitabschnitts Δt berechnet.
|
F1
=
(v2
/
v) · F → = F2/G2*$K$2
F2
=
- (v1
/v)·
F → = -E2/G2*$K$2
a1
= F1/m → = A3/$M$2
a2
= F2/m → = B3/$M$2
|
v1
= a1· Δt + u1 →
= C3*$L$2+E2
v2
= a2· Δt + u2 →
= D3*$L$2+F2
v
= √(v12+v22) →
= WURZEL(E3^2+F3^2)
tnach
= tvor+ Δt → =
H2+$L$2
|
|
x
= 0,5 · a1 · Δt2 + u1
· Δt + x0 → = 0,5*C3*$L$2^2 +
E2*$L$2 + I2
y
= 0,5 · a2 · Δt2 + u2
· Δt + y0 → = 0,5*D3*$L$2^2 +
F2*$L$2 + J2
|
Mit
der Taste „Zeilenwechsel“ wird der Eintrag einer
Rechenanweisung beendet. Es erscheint dann anstelle der eingetragenen
Formel das Rechenergebnis. Mit einem einfachen Klick auf das
Rechenergebnis kann die zugehörende Formel oben im
Tabellenfenster neben „fxΣ
=“
sichtbar gemacht werden. Bei einem Doppelklick tritt an die Stelle
des Rechenergebnisses die zugehörende Formel.
Mit
„Einfügen-Kopieren“ überträgt man nicht
das Rechenergebnis, sondern die Formel.
Zur
Berechnung der Werte am Ende des zweiten, dritten, vierten... und n.
Δt müssen weitere n Zeilen folgen, die sich von der
vorangehenden Zeile nur dadurch unterscheiden, dass die Indices der
Variablen ohne „$“ um 1 erhöht sind.
Das
Anlegen dieser Zeilen geschieht in folgender Weise:
Die
1. Spalte der dritten Zeile wird angeklickt und damit ein Rahmen um
die dort vorhandene Eintragung gesetzt. Dieser Rahmen wird
anschließend bei gedrückter Maustaste (Linkstaste) mit dem
Mauszeiger in der Rahmenmitte bis zur Spalte J geführt (siehe
Abb. 1.4.11 ).
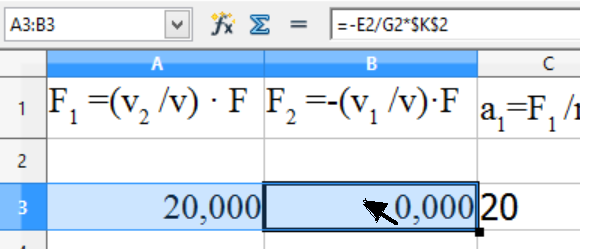
1.4.11
Danach
zieht man mit der Maus den rechten unteren Eckpunkt des Rahmens bei
gedrückter Maustaste (Linkstaste) nach unten, wobei ein roter
Rahmen aufgespannt wird. Nach der Freigabe der Maustaste wird das
umrahmte Feld mit mit den Ergebnissen der darin neu angelegten Zeilen
ausgefüllt.
Wenn
man von den Indices der Variablen ohne „$“ absieht,
könnte man die neu angelegten Zeilen als Kopien der dritten
Zeile bezeichnen. Die genannten Indices werden jedoch von Zeile zu
Zeile um 1 vergrößert. Dementsprechend sind die
Rechenergebnisse einer Zeile die Anfangswerte für die
Berechnungen in der nächsten Zeile.
In
der 3. Zeile stehen nun die Werte nach dem 1. Zeitabschnitt Δt,
in der 4. Zeile die Werte nach dem 2. Zeitabschnitt Δt usw..
Die
Spalten I(x-Werte) und J(y-Werte) werden zur grafischen Darstellung
ausgewählt. Nach Anklicken des Buchstabens I (Linkstaste)
wird der Mauszeiger bei gedrückter Maustaste nach J geführt.
Nach Wahl von „Diagramm“ unter „Einfügen“
erscheint das erste Dialogfeld der Abb. 1.4.12 und nach Anklicken von
„XY“ das nächste in dieser Abbildung gezeigte
Dialogfeld.
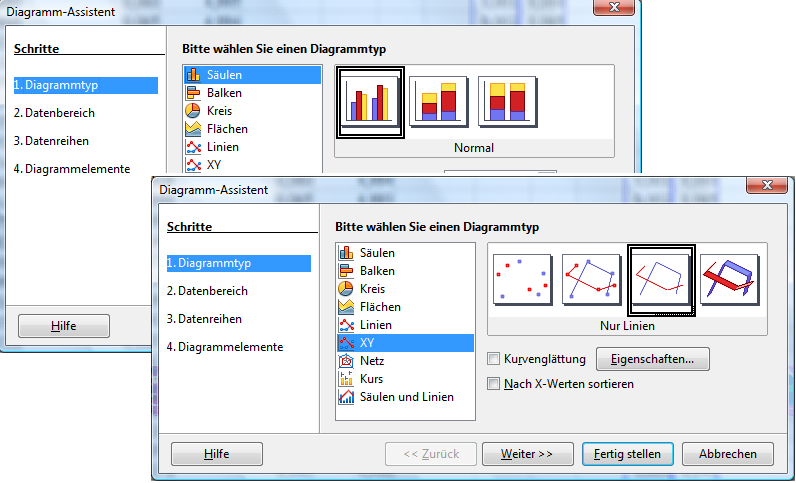
Abb.
1. 4.12
Mit
„Nur Linien“ und „Fertig stellen“
wird die in der Abb. 1.4.13 sichtbare kreisförmige Bahn gezogen.
Sie weicht etwas von einer Kreisbahn ab. Dies ist auf
Rechenungenauigkeiten zurückzuführen.
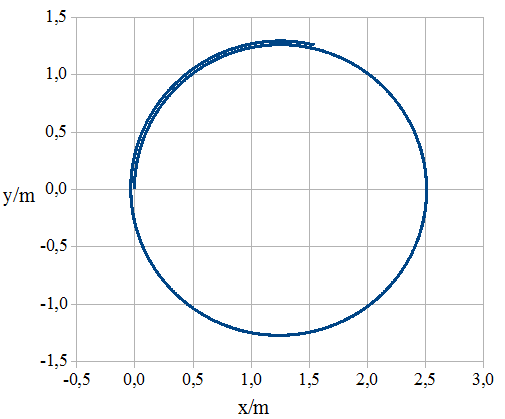
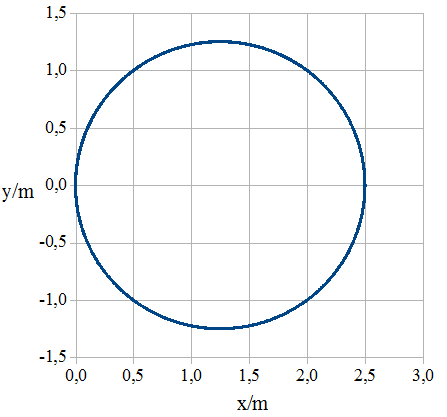
Abb.
1. 4.13 Abb.
1. 4.14
Eine
höhere Rechengenauigkeit wird erreicht, wenn statt der
Beschleunigung zu Beginn eines kleinen Zeitabschnitts Δt die
Beschleunigung in der Mitte von Δt zur Berechnung genommen
wird.
Für
die Änderung Δa der Beschleunigung in Δt/2 kann
geschrieben werden:
Δa
≈ (avor Δt
– anach
Δt ) / 2
→
aMitte
≈
avor
Δt
+
(avor
Δt
– anach
Δt
)
/ 2
Da
a nach Δt zunächst unbekannt ist, wird nicht
das Δa des aktuellen Δt, sondern das zum vorhergehenden
Δt genommen. Zur Korrektur mit Δa werden in der Tabelle
unter der 5. Zeile alle Zeilen gelöscht. Dann erhalten die unter
C und D in der fünften Zeile stehenden Anweisungen
(Beschleunigungen) als Δa die Korrekturglieder +(C4-C3)/2 und
+(D4-D3)/2. Hiernach wird die fünfte Zeile bis zur Zeile 2000
kopiert.
Die
mit den neuen Werten berechnete Bahn (siehe Abb. 1. 4.14) ist ein
Kreis mit einem 1,25 m-Radius. Die Korrektur ist so gut, dass noch
bei einem 10 fach größeren Wert von Δt ( Δt =
0,01) eine ordentliche Kreisbahn entsteht.
Ist
das Fenster, in dem das Diagramm liegt, durch Doppelklick aktiviert
(grauer Rand), dann können mit „Einfügen-Titel“
Titel hinzugefügt und die Achsen beschriftet werden ( hier y/m
und x/m). Ein Gitternetz ist mit „Einfügen-Gitter“
machbar und nach einem Rechtsklick im Diagrammbereich kann mit
„Format-Position und Größe“ die Länge und
Breite des Diagrammfeldes festgelegt werden. Die hier berechnete Bahn
ist nur dann als Kreisbahn erkennbar, wenn die Strecken gleich lang
sind, die den Einheiten auf der x- und y-Achse zugeordnet sind. Mit
einem Rechtsklick auf einer Zahl an den Koordinatenachsen werden
Möglichkeiten zur Gestaltung der Zahlenangaben angezeigt.
Der
in der Abb. 1. 4.16 ablesbare Radius r = 1,25 m ist nach der in dem
Kapitel 1.3.11 als Vermutung angegebene Gleichung F = m·v2/r
zur Kraft auf einen kreisenden Körper zu erwarten.
F
= m·v2/r →
r = m·v2/ F = 1 kg · 25 m2/ s2/
20N = 1,25 m
Die
Werte in der Spalte G zeigen an, dass die Bahngeschwindigkeit v
konstant ist.
Als
Ergebnis der hier durchgeführten Untersuchung ist festzustellen:
Ein Körper wird auf einer Ebene durch eine zur Ebene
parallele, dem Betrage nach konstante Normalkraft auf einer Kreisbahn
mit konstanter Geschwindigkeit gehalten (G= v ist konstant). Die auf
den Kreismittelpunkt gerichtete Kraft heißt Zentripetalkraft FZ
und die zugehörende Beschleunigung Zentripetalbeschleunigung.
|
Die
Beschleunigung zum Kreismittelpunkt hin wird
Zentripetalbeschleunigung genannt. Zur experimentellen Ermittlung
ihres Betrags lassen wir eine Kugel auf der Experimentierwippe
kreisen (siehe Abb. 1.4.15).
|

Abb.
1.4.15
|
Das
Diagramm beschreibt den Weg s des Punktes P, der senkrechten
Projektion des kreisenden Körpers B auf einen durch den
Kreismittelpunkt gehenden Pfeil. Dem Bewegungsdiagramm kann mit
bekannten Computerprogramm Cassy-Lab der Firma LD-DIDACTIC eine
Parabel angepasst und der zu ihr gehörende Funktionsterm
bestimmt werden. Für sehr kurze Zeiten t nach der Kehrtwende von
P am linken Umkehrpunkt gilt für den Weg s diese Punktes:
s
= ½ ·a ·t2
( a = |a|
)
Für
die Parabel in der Abb. 1.4.15 wurde s = (1,51 m/s2)
·
t2
erhalten.
Folglich hat die Zentripetalbeschleunigung den Wert 3,02 m/s2.
Nach
den am Diagramm ablesbaren Werten (Umlaufzeit
= 1,32 s , Bahnradius =14 cm) ist v2/r
= 3,1
m/s2.
Der
geringe Unterschied zwischen den beiden Werten 3,02 m/s2
und
3,1 m/s2
ist
auf Ungenauigkeiten bei der Messung zurückzuführen.
Der
Funktionsterm der Parabel, welche die Bewegung der Projektion P bei
kleinem s beschreibt, soll nun anhand der Abb. 1.4.16 hergeleitet
werden. Das der Kreisbahn zugeordnete Dreieck ABC ist nach dem Satz
des Thales ein rechtwinkliges Dreieck. Es vergeht die Zeit t, während
P den Weg s zurücklegt. Der Kreisbogen AB weicht bei kleinem t
nur sehr wenig von der Kathete AB ab. Es gilt somit nach dem
Kathetensatz:
s·
(2 · r) = ( v·t)2 → s = [(v2/r)
/2]·t2
↓
s
= (a /2) · t2
↓
a
= v2/r → |FZ| = m·
v2/r
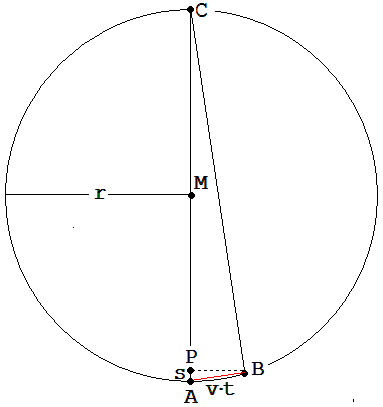
Abb.
1. 4.16
Für
die Zentripetalkraft wird oft die Gleichung F = m·ω2·r
angegeben. ω ist die
Winkelgeschwindigkeit, sie beschreibt den Winkel (im
Bogenmaß), der in einer Zeiteinheit von der Strecke
überstrichen wird , welche den kreisenden Körper mit dem
Drehpunkt verbindet.
ω
= 2·π/T , v = 2·π·r/T
→ v = ω·r;
F =
m ·
v2/r
=
m·(ω·r)2/r
=
m·ω2·r
Aufgaben
Zur Behandlung der hier gegeben
Aufgaben muss das Additionsgesetz der Kräfte bekannt sein,
welches erst in den folgenden Kapiteln behandelt wird. Dieses Gesetz
besagt: Wirken
auf einen Körper K zwei Kräfte F1
und
F2
,
dann verhält sich der Schwerpunkt von K so, als ob nur eine der
Vektorsumme von F1
und
F2
gleichende
Kraft
F3
auf
ihn einwirke.
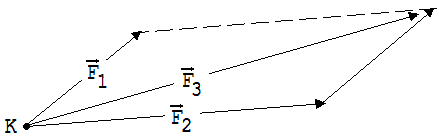
Abb.
1.4.17
1.
Ein mit Wasser gefüllter Eimer wird in einer vertikalen
Ebene auf einer Kreisbahn mit r = 0,8 m um einen Punkt M gedreht.
Welche Geschwindigkeit muss der Eimer am höchsten Punkt seiner
Bahn mindestens haben, wenn das Wasser nicht auslaufen soll ?
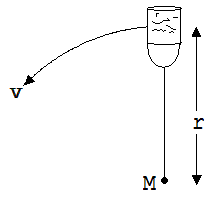
Abb.
1. 4.18
2.
Wenn die Straße glatt ist (vernachlässigbare Reibung),
dann muss sie in einer Kurve nach dem äußeren Kurvenrand
hin ansteigen, damit ein Auto nicht aus der Kurve heraus rutscht.Wie
groß muss der Anstiegswinkel α in einer Kurve mit dem
Radius r = 50 für ein Auto mit 100 km/h sein ?
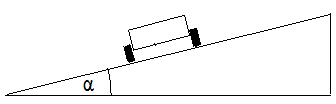
Abb.
1.4.19
3.
Mit
v = 20 km/h fährt ein Radfahrer in eine Kurve, deren Radius r =
20 m beträgt. Mit welchem Winkel α legt sich der Radfahrer
hierbei in die Kurve ?
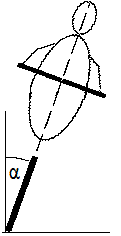
Abb.
1.4.20
4.
Am oberen Ende eines rotierenden senkrechten Stabes ist eine Kugel
mit einem Faden der Länge L = 50 cm angebunden. Sie dreht sich
mit der Winkelgeschwindigkeit ω = 10 ·1/s. Welchen
Winkel α bildet der 4Faden mit dem Stab ?
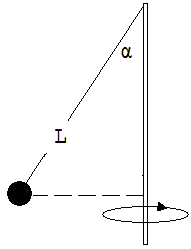
Abb.
1.4.21
5.
Auf
die höchste Stelle eines Rohres mit dem Radius r = 0,5 m wird
ein kleiner Experimentierwagen gesetzt. Nach einem ganz leichten Stoß
rollt er reibungsfrei abwärts. Bei welchem Winkel α löst
er sich vom Rohr ?
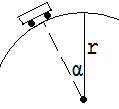
Abb.
1.4.22