1.3. Grundbegriffe der Mechanik

1.3.1 Gleichförmige Bewegung

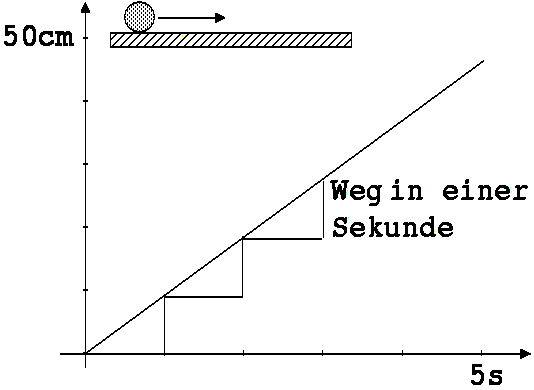
Wir lassen eine Kugel über die waagrecht eingestellte Wippe rollen. Es entsteht hierbei ein geradliniges Diagramm (siehe Abb. 1.3.1), an dem zu erkennen ist, dass in gleichen Zeiten gleiche Wege zurückgelegt werden.

Eine Bewegung mit dieser Eigenschaft heißt gleichförmig.

Abb. 1.3.1

Abb. 1.3.2: Hotelschiff auf dem Rhein bei Kaub in gleichförmiger Fahrt

Der zurückgelegte Weg s ist der Bewegungszeit t proportional. Das konstante Verhältnis aus Weg und Zeit trägt den Namen Geschwindigkeit v = s/t. Es beschreibt die Strecke, welche in einer Zeiteinheit zurückgelegt wird.

Siehe auch:

1.3.2 Der Trägheitssatz

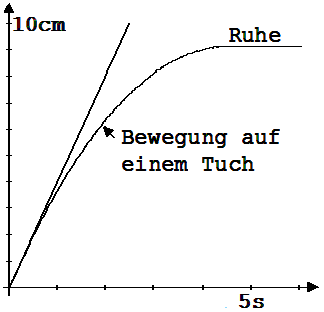
Abb. 1.3.3

Eine Eisenkugel wird auf einem Tuch angestoßen, welches zuvor auf die Glasplatte der Wippe gelegt wurde. Das s-t-Diagramm hat nun einen gekrümmten Verlauf (siehe Abb. 1.3.3). Die Krümmung der Kurve fällt geringer aus, wenn ein weniger raues Tuch gewählt wird. Die Kugelbewegung passt sich einer gleichförmigen-geradlinigen Bewegung umso mehr an, je weniger die Rollbahn durch Unebenheiten auf sie einwirkt. Hieraus folgern wir den sogenannten Trägheitssatz:

Ein Körper verharrt in Ruhe oder in gleichförmig-geradliniger Bewegung, wenn seine Umgebung nicht auf ihn einwirkt.

Die folgenden zwei Beispielen sollen zur Veranschaulichung dieses Gesetzes dienen.

1. Ein Experimentierwagen steht auf einer Glasplatte, die auf dem Experimentiertisch liegt. Wird an der Glasplatte gezogen, dann bleibt der Wagen an seinem Ort (siehe Abb. 1.3.4).

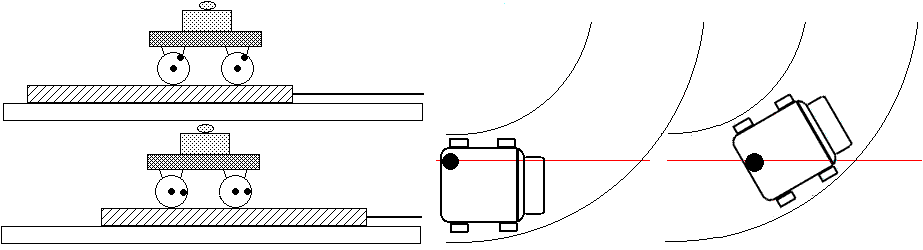
Abb. 1.3.4                                                    Abb. 1.3.5  

2. Man denke sich einen Lastwagen in einer Linkskurve. An der linken Ecke der Ladefläche steht ein einzelner Kartoffelsack. Dieser Sack verharrt ohne äußeren Zwang in einer gleichförmigen Bewegung. Infolgedessen rutscht er von der einen Ecke in die gegenüberliegende Ecke der Ladefläche (siehe Abb. 1.3.5).

1.3.3. Die Masse

Eine rollende Eisenkugel wird im Gegensatz zu einer Glaskugel gleichen Volumens bei einem Stoß auf ein Stück Kreide nur geringfügig abgelenkt. Die Eisenkugel reagiert weniger empfindlich auf ein Hindernis als die Glaskugel. Man sagt, sie sei träger als die Glaskugel.

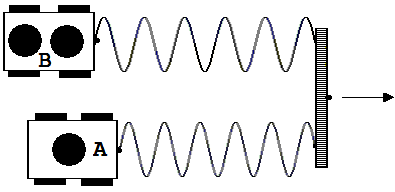
Abb.1.3.6

Abb.1.3.6 zeigt, wie man zwei Körper hinsichtlich ihrer Trägheit vergleichen kann. Zwei zunächst nebeneinander stehende Experimentierwagen mit unterschiedlicher Ladung sind mit gleichartigen Schraubenfedern an einem Stab angebunden. Wird am Stab gezogen, dann folgen die beiden Wagen, wobei der Wagen B anfangs hinter dem Wagen A zurückbleibt. B ist träger als A.

Soll die Trägheit eines Körpers K beschrieben werden, dann vergleicht man K mit einem als kg bekannten Einheitskörper. Es wird die Menge von kg-Körpern angegeben, die zusammengenommen genauso träge sind wie K. Diese Menge heißt Masse von K. In Abb. 1.3.7 ist eine Waage dargestellte, mit der normalerweise Massenvergleiche durchgeführt werden.

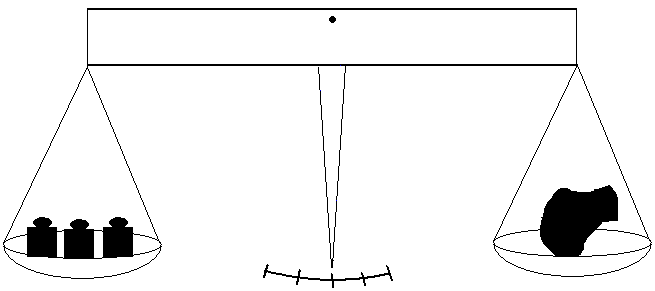
                                         Abb. 1.3.7                                                          Abb. 1.3.8

Abb. 1.3.8: Keltische Waage (Grabfund Frankfurt-Fechenheim, 2 Jhdt. v. Chr.)

Dieser Vergleich ist möglich, weil zwei Körper gleicher Masse sich in ihrer Wirkung auf einen Hebel nicht unterscheiden.

Man sagt: Die schwere Masse ist gleich der trägen Masse.

In Verbindung mit dem Wort Masse wird oft der Begriff Dichte genannt. Die Dichte ρ eines Körpers K ist durch den Quotienten Masse von K / Volumen von K definiert. Sie beschreibt die Masse einer Volumeneinheit.

Folglich gilt: Masse = Volumen · Dichte

1.3.4 Schwerpunkt und Schwerpunktsatz, Impuls und Impulssatz

Auf der waagrecht eingestellten Experimentierwippe rollt eine Glaskugel auf zwei andere ruhende Glaskugeln. Trotz des Stoßes zeichnet der Rechner ein lineares Diagramm (siehe Abb. 1.3.9).

Was wird hier angezeigt ?

Wenn die drei Kugeln gleicher Masse K₁, K₂ und K₃ an einem Punkt P (siehe Abb. 1.3.10) zusammen liegen, dann ist deren gemeinsamer Abstand x von der einen Schmalseite der Wippe maßgebend für ihre Wirkung auf die Wippe. Sind sie über die Platte verteilt, dann wird die Drehung der Wippe durch den Mittelwert x der Abstände x₁, x₂ und x₃ bestimmt. Der Punkt, dessen Koordinaten durch Mittelwertbildung aus den Koordinaten der drei Kugeln gewonnen wird, heißt Schwerpunkt (Massenmittelpunkt) P der drei Kugeln. Sein Abstand von einer Schmalseite der Wippe wird angezeigt.

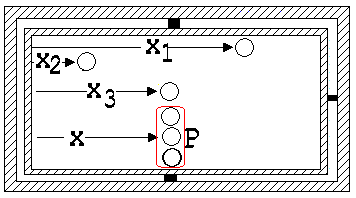
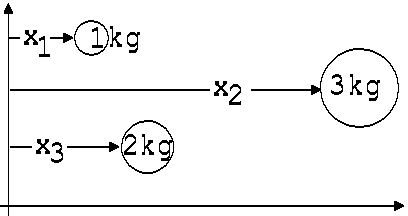
Abb. 1.3.10                                                    Abb. 1.3.11

x = (x₁ + x₂+ x₃ ) /3

Bei unterschiedlichen Massen müssen die Kugeln zunächst gedanklich in Teile gleicher Masse zerlegt werden. Erst dann können die Schwerpunktkoordinaten durch Mittelwertbildung berechnet werden (siehe Abb. 1.3.11).

x = (1· x₁ + 3· x₂ + 2 · x₃ )/ 6 = (1kg· x₁ + 3kg · x₂ + 2 kg· x₃ )/ 6 kg

x = (m₁· x₁ + m₂ · x₂ + m₃ · x₃ )/ (m₁ + m₂ + m₃)

Definition des Schwerpunkts (Massenmittelpunkts):

Wir denken uns ein System in Teile gleicher Masse eingeteilt. Aus den x-, y- und z-Koordinaten werden Mittelwerte gebildet. Der Punkt mit diesen Mittelwerten als Koordinaten heißt Schwerpunkt des Systems.

Das in Abb. 1.3.9 gezeigte Experiment lässt den Schluss zu:

In einem abgeschlossenen System (System ohne Wechselwirkung mit seiner Umgebung) ist der Schwerpunkt entweder in Ruhe oder er bewegt sich gleichförmig.

Diese als Schwerpunktsatz bekannte Aussage ist als eine Verallgemeinerung des Trägheitssatzes zu sehen. Besonders eindrucksvolle Experimente zum Schwerpunktsatz sind in den Abbildungen 1.3.12 und 1.3.13 dargestellt.

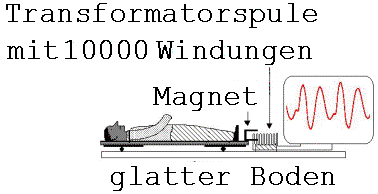
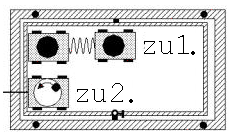
    Abb. 1.3.12                                                                   Abb. 1.3.13

Zu Abb. 1.3.12:

Ein Schüler liegt auf einem Brett, welches auf Wasserrohren aus Hartplastik gelagert ist. Zu empfehlen sind die in Baumärkten angebotenen orangefarbenen Rohre, welche in der Erde verlegt werden. Wenn Blut aus einer Herzkammer gepumpt wird, dann bewegt sich der Körper zur Erhaltung des Schwerpunkts entgegen der Strömungsrichtung. Diese Bewegung wird von einem Rechner in einem Ballistokardiogramm dargestellt. Zur Registrierung der Verschiebung ist am einen Ende des Bretts ein Hufeisenmagnet befestigt, dessen einer Pol in eine Transformatorspule mit 10000 Windungen hineinragt.

Zu Abb. 1.3.13:

1. Zwei Experimentierwagen sind mit einer Schraubenfeder gekoppelt. Wird der eine angestoßen, dann wechseln die beiden fortwährend ihre Geschwindigkeiten. Der zweite ruht, der erste fährt, dann ruht der erste und der zweite fährt usw.. Trotzdem entsteht ein lineares Diagramm.

2. Auf einem Experimentierwagen steht eine Kristallisierschale. Während der Wagen an einem Faden festgehalten wird, stößt der Experimentator eine in ihr liegende Kugel zur Rotation an. Der Wagen bewegt sich nach seiner Freigabe ruckartig über die Bahn, wobei ein lineares Diagramm zur Bewegung des Schwerpunkts geschrieben wird. Der Wagen ist beim Rücklauf der Kugel schneller als beim Vorlauf der Kugel. Die Geschwindigkeit des Schwerpunkts bleibt trotz der schwankenden Wagengeschwindigkeit konstant.

Kann anhand des Schwerpunktsatzes auf die Wagengeschwindigkeit geschlossen werden?

Es ist davon auszugehen, dass man die Schwerpunktgeschwindigkeit bei Kenntnis der Geschwindigkeiten vom Wagen und der Kugel berechnen kann. An einer Gleichung zur Berechnung der Schwerpunktgeschwindigkeit v_S wird man wegen v_S = konstant sehen können, wie die Wagengeschwindigkeit v_W von der Geschwindigkeit der Kugel v_K abhängt. Zur Berechnung von v_S muss zunächst die Verschiebung Δx bestimmt werden, die der Schwerpunkt in einem kleinen Zeitabschnitt Δt erfährt.

Δx = (m_K · Δx_K + m_W · Δx_W) / (m_K + m_W )

Um Δx_K und Δx_W ändern sich in der Zeit Δt die Abstände der Kugel und des Wagens vom linken Ende der Wippe. Folglich gilt für die Schwerpunktgeschwindigkeit v_S:  v_S = Δx/ Δt = (m_K · Δx_K/ Δt + m_W · Δx_W / Δt) / (m_K + m_W )

Δx_K / Δt = Geschwindigkeit v_K, mit der sich die Kugel von der Schmalseite der Wippe entfernt, Δx_W / Δt = Wagengeschwindigkeit v_W

v_S = (m_K · v_K + m_W · v_W) / (m_K + m_W )

Wegen v_S= Konstante können wir schreiben:

Die Summe m_K · v_K + m_W · v_W ist konstant.

Wegen der Konstanz dieser Summe kommt der Wagen bei einer zurück rollenden Kugel (v_K < 0) schneller voran, als bei einer vorwärts rollenden Kugel.

Das Produkt aus einer Masse m und deren Geschwindigkeit v trägt den Namen Impuls oder Bewegungsgröße. Nach dem Schwerpunktsatz gilt für jedes abgeschlossene System das als Impulssatz bekannte Gesetz:

Die Summe aus den Impulsen seiner Teile ist konstant.

Experimente zum Impulssatz

In Abb. 1.3.14 sehen wir auf der Wippe einen zunächst ruhenden Wagen mit einem darauf befestigten Tafelschwamm (Gesamtmasse m = 200g ). Die Wippe ist zum Reibungsausgleich so aufgestellt, dass sie nach rechts geringfügig abfällt. Wird mit einem Luftgewehr in den Schwamm geschossen, dann bewegt sich der Wagen anschließend gleichförmig mit der Geschwindigkeit v_W. v_W = Δx_W/ Δt kann anhand des Diagramms in der Abb. 1.3.15 bestimmt werden.

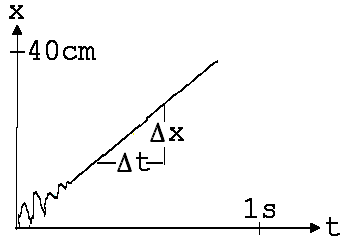
                                              Abb. 1.3.14                                                                   Abb. 1.3.15

Der Impulssatz ermöglicht die Berechnung der Geschossgeschwindigkeit.

Die Impulssumme vor dem Einschuss ist gleich dem Impuls m_G · v_G des Geschosses, denn anfangs steht der Wagen. Danach ist die Impulssumme gleich dem Impuls des Wagens mit Schwamm und dem in ihm steckenden Geschoss.

m_G · v_G = (m_W + m_G )· v_W

Ist m_G erheblich kleiner als m_W dann gilt: m_G · v_G ≈ m_W · v_W   →   v_G ≈  m_W · v_W /m_G

m_G · v_G ist maßgebend für die Stärke des Stoßes (Impulses), den die Luftgewehrkugel dem Wagen erteilt. Der Name „Impuls“ für das Produkt m·v erscheint mit Blick auf das hier beschriebene Experiment angemessen.

Eine eindrucksvolle Demonstration zum Impulssatz ist mit dem in Abb. 1.3.16 sichtbaren Raketenwagen möglich. Auf einem insgesamt 200 g schweren Experimentierwagen ist ein sogenannter Heuler (Feuerwerkskörper) befestigt. Wird der Heuler angezündet, dann stößt er nach hinten heißes Gas aus und der Wagen rollt nach vorne. Das zugehörige s-t-Diagramm ist eine Parabel (Versuch auf der Wippe ).

Abb. 1.3.16

Wenn die Rollreibung des Wagens ausgeschlossen werden kann, dann ist die Summe aus dem Impuls des Gases und dem Impuls des Wagens gleich 0, denn das als Gas entweichende Material und der Wagen waren anfangs in Ruhe. Beide Impulse stimmen in ihren Beträgen überein, haben aber verschiedene Vorzeichen.

Aufgaben

1. Auf einem ruhenden, m_W = 100 kg schweren Wagen steht eine m_P = 90 kg schwere Person. Diese Person geht 5m von dem einen Ende des Wagens zum anderen.

Welchen Weg legt hierbei der Wagen auf einer waagrechten Bahn zurück, wenn von der Rollreibung abgesehen wird ?

Abb. 1.3.17

Anmerkung zur Lösung:

Den gemeinsamen Schwerpunkt x des Wagens W und der Person P erhält man nach: x = (x_w· m_w+ x_P· m_P) / (m_W + m_P), x_W und x_P sind Schwerpunktkoordinaten des Wagens und der Person.

2. Über eine horizontale Schiene rollt ein mit Kartoffeln beladener Wagen mit der Geschwindigkeit v₀ = 5 m/s. Die gesamte Masse des Wagens m₀ beträgt 250 kg. In den rollenden Wagen fallen zwei Säcke Kartoffeln mit je m = 50 kg. Welche Geschwindigkeit v hat der Wagen nach diesem Ereignis, wenn die Rollreibung vernachlässigbar ist ?

3. Auf einer horizontalen ebenen Fläche stehen zwei Experimentierwagen mit den Massen m₁ = 150 g und m₂ = 250 g (siehe Abb. 1.3.18 ). Am Wagen der Masse m₁ ist eine gestauchte Schraubenfeder befestigt, welche gegen den schwereren Wagen drückt und dabei einen Faden straff hält, der zwischen den beiden Wagen aufgespannt ist. Wenn der Faden zerschnitten wird, dann löst sich der leichtere Wagen mit der Geschwindigkeit v₁ = 2m/s vom anderen Wagen.

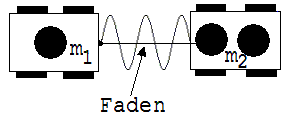
Abb. 1.3.18

Welche Geschwindigkeit v₂ hat der Wagen mit der Masse m₂ nach der Trennung der Fahrzeuge ?

1.3.5 Vektoren

Man stelle sich nun einen mit der Geschwindigkeit v rollenden Wagen vor (siehe Abb. 1.3.19), der wie ein Rollbrett nach allen Seiten frei beweglich ist. In den auf diesem Wagen liegenden Schwamm schlage von der Seite her ein Luftgewehrgeschoss der Masse m_G mit der Geschwindigkeit u ein. Der Einschlag des Geschosses ändert in diesem Fall auch die Bewegungsrichtung des Wagens. Damit die Anwendung der an eindimensionalen Bewegungen gewonnenen Gesetze möglich ist, wird das Geschoss und der Experimentierwagen auf die beiden Achsen des Koordinatensystems senkrecht projiziert. Die Projektionen bewegen sich vor dem Einschlag der Kugel in x-Richtung mit u₁ und v₁ und in y-Richtung mit u₂ und v₂. Nach dem Einschlag der Kugel bewegt sich der Wagen zusammen mit der Kugel mit der Geschwindigkeit w₁ in x- und w₂ in y-Richtung.

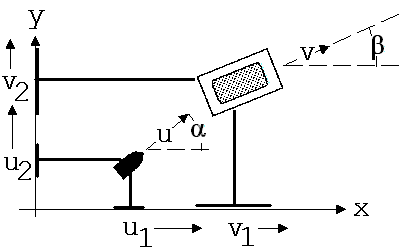
Abb. 1.3.19: Draufsicht     

Der Impulssatz gilt für beide Bewegungsrichtungen !

m_G · u₁ + m_W · v₁ = (m_G + m_W) · w₁;        m_G · u₂ + m_G · v₂ = (m_G + m_W) · w₂

Aufgabe: Gegeben sei m_G = 0,5 g,  α = 30°,   u = 60 m/s und  m_W = 200g,   β = 20°,    v = 0,5 m/s

Welche Geschwindigkeit und welche Bewegungsrichtung hat der Schwerpunkt des Wagens nach dem Stoß durch die Kugel ?

Zur Anwendung des Impulssatzes müssen anhand der Angaben die Geschwindigkeiten u₁, u₂, v₁, v₂ beider Gegenstände in x und y-Richtung berechnet werden. Zu diesem Zweck werden die Geschwindigkeiten vor dem Stoß durch Pfeile veranschaulicht. Die Pfeile werden so angelegt, dass sie nicht nur die Bewegungsrichtungen der Gegenstände, sondern auch noch deren Geschwindigkeiten mit ihren Längen anzeigen (siehe Abb. 1.3.20). Die Länge L eines Pfeils kann z.B. gleich dem Weg sein, den ein Körper in 1s, in 0,1s oder in 0,01s zurücklegt. Je nach gewählter Zeit repräsentiert ein solcher Pfeil die Geschwindigkeiten v = L/1 s bzw. v = L/0,1 s bzw. v = L/0,01 s. Man sollte sich den Pfeil wie einen Zahlenstrahl skaliert vorstellen, so dass man an der Spitze den zugeordneten Wert ablesen kann.

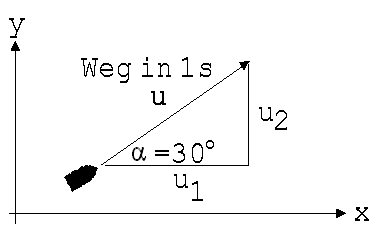
Abb. 1.3.20

Derartige Pfeile setzt man immer dann ein, wenn neben der Angabe eines Maßes noch eine Richtungsbeschreibung nötig ist, man nennt sie Vektoren.

u₁ = u · cos α;    u₂ = u · sin α

Auf gleiche Weise erhält man für den Wagen: v₁ = v · cos β;    v₂ = v · sin β

Für die Geschwindigkeiten des Wagens nach dem Stoß in x- und y-Richtung gilt:

(m_W + m_G ) · w₁ = m_G· u · cos α + m_W · v · cos β

(m_W + m_G ) · w₂ = m_G· u · sin α + m_W · v · sin β

↓

w₁ = ( m_G· u · cos α + m_W · v · cos β ) / (m_W + m_G) = 0,598 m/s

w₂ = ( m_G · u · sin α + m_W · v · sin β ) / ( m_W +m_G ) = 0,245 m/s

Mit den Ergebnissen für w₁ und w₂ ist die Aufgabe fast gelöst. Es fehlen nur noch Angaben über die Bewegungsrichtung und die Gesamtgeschwindigkeit w des Wagens nach dem Stoß. Zu diesem Zweck wird der zu w₁ und w₂ passende Geschwindigkeitsvektor dargestellt (siehe Abb. 1.3.21). Die Gesamtgeschwindigkeit w (Länge des Pfeils = Betrag des Vektors ) erhält man mit Hilfe des Satzes von Pythagoras. w₁ und w₂ beschreiben die Wege, die nach dem Einschlag der Kugel vom Wagen in einer Sekunde in x- und y-Richtung zurückgelegt werden. Der Pfeil zeigt die Gesamtgeschwindigkeit nach Größe und Richtung an.

w² = w₁² + w₂²  →   w = √ (w₁² +w₂²) = 0,646 m/s

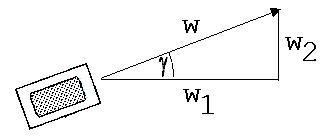
Abb. 1.3.21

Die Bewegungsrichtung des Wagens nach dem Stoß bildet mit der x-Richtung den Winkel γ .

tan(γ) = w₂ / w₁ = 0,4096, γ = 22,27°

Vektorkoordinaten und Vektorkomponenten

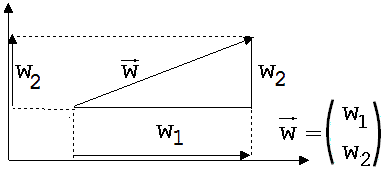
Abb. 1.3.22

Die Geschwindigkeiten in x und y - Richtung werden Vektorkoordinaten genannt. Allgemein versteht man unter den Koordinaten eines Vektors die Größen, die den senkrechten Projektionen des Vektors auf die Achsen des Koordinatensystems zugeordnet werden (siehe Abb. 1.3.22 ). Ist eine solche Projektion der Koordinatenachse entgegen gerichtet, dann ist die zugehörende Vektorkoordinate negativ. Die genannten Projektionen heißen Vektorkomponenten.

Die Beschreibung eines Vektors geschieht meistens mit der Angabe seiner Koordinaten, die man normalerweise zu einer mit Klammern eingefassten Säule (oben die x-Koordinate, dann die y-Koordinate und schließlich bei räumlichen Vorgängen noch die z-Koordinate ), manchmal aber auch aus drucktechnischen Gründen in einer Reihe anordnet, z.B. {w₁ ; w₂ ; w₃}. Aus dieser Beschreibungsform geht hervor, dass man Vektoren dann als einander gleich ansieht, wenn sie in diesen Koordinaten übereinstimmen. Dies bedeutet Übereinstimmung in Richtung und Länge, nicht jedoch im Anfangspunkt. Als Zeichen für Vektoren sind Buchstaben mit einem kleinen aufgesetzten Pfeil oder fett gedruckte Buchstaben üblich. Wird ein solcher Buchstabe in Betragszeichen gesetzt, dann meint man das dem Vektor zugeordnete Maß (Vektorbetrag). Dieser entspricht seiner Länge.

Beispiel: |w| = √ (w₁² +w₂² ).

Vektorsumme und Vektordifferenz

Zu dem in der Abb. 3.19 skizzierten Experiment werden die Geschwindigkeiten u, v und w angegeben. Ihnen werden Geschwindigkeitsvektoren u ={u₁; u₂}; v ={v₁; v₂}; w ={w₁; w₂} und Impulsvektoren {m_G·u₁; m_G·u₂}; { m_W ·v₁; m_W · v₂}_; {(m_G+m_W)·w₁; (m_G+m_W)·w₂} zugeordnet.

{(m_G+m_W) ·w₁; (m_G+m_W) ·w₂} = { m_G·u₁ + m_W·v₁; m_G·u₂ + m_W·v₂} wird Summe der Vektoren {m_G·u₁;  m_G·u₂} und { m_W ·v₁;  m_W ·v₂} genannt.

Die Vektorsumme zweier Vektoren a und b erhält man demnach, indem man die entsprechenden Koordinaten von a ={a₁; a₂; a₃} und b ={b₁; b₂; b₃}addiert.

a + b = {a₁ + b₁ ; a₂ + b₂ ; a₃ + b₃}

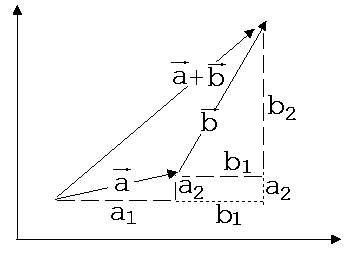
Abb. 1.3.23

Der Summenvektor zeigt vom Fuß des Vektors a zur Spitze des Vektors b, wenn der Fuß von b die Spitze von a berührt (siehe Abb.1.3.23).

a - b = {a₁- b₁ ; a₂ - b₂ ; a₃ - b₃} heißt Vektordifferenz. Man erhält den Differenzvektor, indem man b mit seiner Spitze an die Spitze von a fügt (siehe Abb.1.3.24). Der Vektor vom Fuß des Vektors a zum Fuß des Vektors b ist a – b.

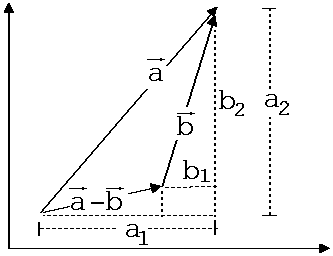
Abb. 1.3.24

Das Produkt und der Quotient eines Vektors mit einer Zahl

Anstelle von {m_G · u₁; m_G · u₂} und { m_W · v₁; m_W · v₂} schreiben wir m_G · {u₁; u₂} und m_W · {v₁; v₂}. Hieran ist erkennbar, wie das Produkt aus einem Vektor a und einer Zahl m definiert ist.

m · a = m·{a₁ ; a₂ ; a₃} = {m · a₁ ; m · a₂ ; m · a₃}

Man nennt die hier beschriebene Multiplikation eines Vektors mit einer Zahl skalare Multiplikation. Sie bewirkt eine Streckung des Vektors a um m (siehe Abb. 1.3.25).

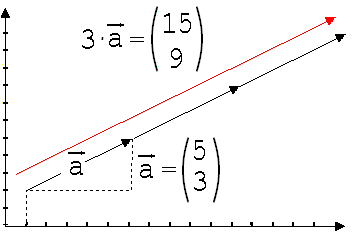
Abb. 1.3.25

Bei Anwendung des Impulssatzes auf den Zusammenstoß zweier Körper mit den Massen m₁ und m₂ im Raum mussten bisher drei Gleichungen geschrieben werden:

Von nun an soll das Wort Impuls für den Impulsvektor stehen. Nach der Definition des hier beschriebenen Produkts m · a ist man geneigt, nach einem entsprechenden Quotienten zu fragen. Ein Quotient a /m (Vektor a durch eine Zahl m) soll so beschaffen sein, dass folgendes gilt: (a/m) · m = a. Dementsprechend gilt: a/ m = (1/m) · a. Teilt man einen Vektor a durch seinen Betrag |a|, dann erhält man einen Einheitsvektor, einen Vektor mit dem Betrag 1. Beispiel: a = {4; 3 }; |a| = √ (16 + 9) = 5 → a / |a| = { 4/5; 3/ 5}

Das Skalarprodukt

Bei dem in der Abb. 1.3.19 skizzierten Experiment hat der Wagen vor dem Einschlag der Kugel die Geschwindigkeit v und nach dem Einschlag die Geschwindigkeit w. Der Winkel γ, den die Vektoren w und v einschließen, beschreibt die Richtungsänderung des Wagens infolge des Einschlags.

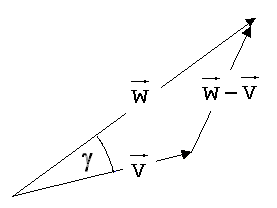
Abb. 1.3.26

Wie groß ist γ ?

Nach dem Kosinussatz gilt: |w-v|² = |w|² + |v|² – 2·|w| · |v| · cos(γ)

(w₁ - v₁)² + (w₂ - v₂)² + (w₃ - v₃)² = w₁² + w₂² + w₃² + v₁² + v₂² + v₃² - 2·|w| · |v| · cos(γ)

↓

{w₁² + w₂² + w₃² +v₁² + v₂² +v₃² } - 2·w₁ · v₁ - 2·w₂ · v₂ - 2·w₃ · v₃ =

={w₁² + w₂² + w₃² + v₁² + v₂² + v₃² } -2·|w|·|v|·cos(γ)

↓

w₁·v₁ + w₂·v₂ + w₃·v₃ = |w|·|v|·cos(γ) → cos(γ) = (w₁·v₁ + w₂·v₂ + w₃·v₃) / (|w|·|v|)

w₁ · v₁ + w₂ · v₂ + w₃ · v₃ heißt Skalarprodukt w · v der Vektoren w und v.

Unter dem Skalarprodukt zweier beliebiger Vektoren a und b versteht man die Summe aus den Produkten entsprechender Koordinaten.

a · b = a₁ ·b₁ + a₂ ·b₂ + a₃ ·b₃

Das Skalarprodukt gleicht dem Produkt der Vektorbeträge und dem Kosinus des eingeschlossenen Winkels (w₁ · v₁ + w₂ · v₂ + w₃ · v₃ )= |w| · |v| · cos(γ) !.

Anmerkung: Der Kosinussatz kann als eine Verallgemeinerung des Satzes von Pythagoras a² + b² = c² aufgefasst werden. Zieht man von a² + b² das Produkt 2·a·b· cos(γ) ab, dann erhält man eine Gleichung, die auch dann gilt, wenn a und b keinen Winkel γ = 90° miteinander bilden.

1.3.6 Definition der Kraft und des Kraftmaßes

Da in einem abgeschlossenen System die Summe aus den Impulsen der Systemteile konstant ist, erscheint eine Änderung dieser Summe als Maß für eine äußere Einwirkung geeignet. Handelt es sich um ein einziges Teilchen, dann ist nur dessen Impulsänderung Δ(m· v) als Merkmal einer äußeren Kraft zu sehen.

Erfährt ein Gegenstand A unter Einwirkung eines Gebildes B eine Impulsänderung, wenn keine Bewegungshemmnisse vorhanden sind, dann sagt man, B übe eine Kraft F (Force) auf A aus.

In dem in Abb. 1.3.27 skizzierten Experiment wird der Impuls eines Teilchens K auf seinem Weg von A nach B während eines Zeitabschnitts Δt unter einem seitlich wirkenden Luftstrom um Δ(m·v) = m·v₂ - m·v₁ geändert. Die Einwirkung ist am besten an der Bewegung der orthogonalen Projektion P der Kugel K auf eine zu Δ(m· v) parallele Gerade zu erkennen (siehe Abb. 1. 3.27).

Abb. 1.3.27

Es gilt: |m· v_P2 - m· v_P1| = Δ|(m·v)|

v_P1 und v_P2 sind die Geschwindigkeiten der Projektion P zu Beginn und am Ende von Δt.

Es ist noch anzumerken, dass die Projektion Pʼ auf eine zu Δ(m·v) senkrechte Gerade eine konstante Geschwindigkeit v_P' hat und demnach keine Impulsänderung erfährt.

Wenn es um ein geeignetes Maß für die Stärke des Windes geht, dann muss man feststellen, dass die Impulsänderung von K allein als Maß für die Stärke des Windes ungeeignet ist, denn bei schwachem Wind erreicht man auch eine große Impulsänderung, wenn man sich genügend Zeit lässt. Je kürzer die Zeit Δt für ein bestimmtes Δ(m· v) ist, desto stärker ist der Wind. |Δ(m· v)|/ Δt = Δ(m· v_P)/ Δt erscheint somit als passendes Maß für die Kraft F.

F = |Δ(m· v_P) / Δt|= |Δ(m· v)| / Δt steht für die Änderung des Impulsbetrags während einer Zeiteinheit unter der Bedingung, dass Δ(m· v) / Δt in dieser Zeit konstant gehalten wird. Ihr ordnen wir den Vektor F =Δ(m· v) / Δt zu.

F = Δ(m·v) /Δ t = {Δ(m·v₁) /Δ t; Δ(m·v₂) /Δ t; Δ (m·v₃) /Δ t }

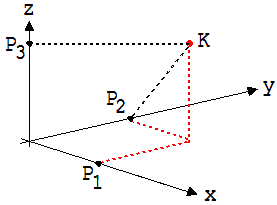
Abb. 1.3.28

m·v₁, m·v₂, und m·v₃ sind die Impulse von P₁ P₂ und P₃ , den Projektionen von K auf die drei Achsen des Koordinatensystems (siehe Abb. 1.3.28 ). Die Projektionslinien bilden mit den Achsen des Koordinatensystems rechte Winkel ! Δ(m· v)/ Δt = Δ(m· v_P)/ Δt steht für die Impulsänderung, die während einer Sekunde bei Konstanz dieses Terms zu erwarten ist.

Ist die Masse m konstant, dann können wir die Impulsvektoren in der Abb. 1.3.27 auch als Geschwindigkeitsvektoren auffassen. Die in der Abbildung sichtbaren Vektoren müssen nur anders skaliert werden. Dem Vektor Δ(m·v) entspricht die Änderung Δv des Geschwindigkeitsvektors. |Δv| / Δt heißt Beschleunigung a (acceleleration) des Teilchens K. |Δv| gleicht der Geschwindigkeitsänderung Δv_P , welche die orthogonale Projektion von K auf eine zum Beschleunigungsvektor a = Δv/ Δt parallele Gerade in der Zeit Δt erfährt.

Die Beschleunigung Δv_P/Δt steht für eine Geschwindigkeitsänderung während einer Zeiteinheit unter der Bedingung, dass Δv_P/Δt in dieser Zeiteinheit konstant bleibt. Bei konstanter Masse kann unter Berücksichtigung von Δ(m· v) = m·Δv geschrieben werden:

F = m ·{Δv₁/Δ t; Δv₂/Δ t; Δv₃/Δ t}= m · a.

a_1, a₂ und a₃ sind die Beschleunigungen von P₁ , P₂ und P₃ (siehe Abb.1.3.28)

1.3.6.1 Messung einer Kraft

Auf der ebenen Glasplatte der Wippe wird ein Experimentierwagen vom Luftstrom eines Föhns angetrieben (siehe Abb. 1.3.29 ).

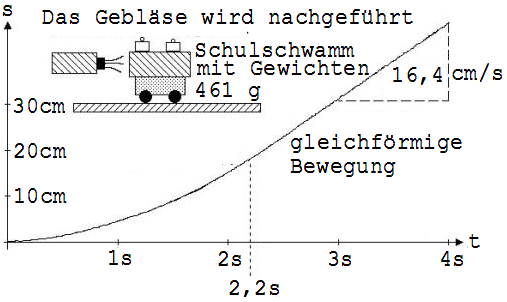
Abb. 1.3.29                                                                                           Abb. 1.3.30

2,2 Sekunden nach Beginn der Bewegung, wird der Föhn vom Wagen abgedreht, die Bewegung wird gleichförmig, was an der linearen Fortsetzung des s-t-Diagramms (Abb. 1.3.30) erkennbar ist. An dem linearen Teil des Diagramms kann die Geschwindigkeit zum Zeitpunkt 2,2 s bestimmt werden. Unter der Einwirkung des Föhns ist die Impulsänderung des Wagens der Zeit des Anblasens proportional, denn die Luft erfährt bei Nachführung des Föhns am Wagen in gleichen Zeiten gleiche Impulsänderungen. F =Δ(m·v)/Δt ist deshalb konstant. Auf den Wagen wirkt nach der Definitionsgleichung F = |Δ(m · v)|/ Δt die Kraft:

F = (0,461 kg ·0,164 m/s) / 2,2 s = 0,034 kg · m/ s²

In 2,2 s hat der Wagen die Impulsänderung 0,461 kg ·0,164 m/s erfahren.

Mit dem Anhängsel (Einheit der Kraft) kg · m/s² wird zum Ausdruck gebracht, wie und in welchen Einheiten die zugehörigen Größen verrechnet werden. Der Leser sollte nicht versuchen, diese Einheit zu veranschaulichen, wie dies zum Beispiel bei den Grundeinheiten Meter oder Kilogramm möglich ist.

1 kg·m/s² wird 1N (Newton ) genannt.

Die Kraft einer gedehnten Schraubenfeder (eines gedehnten Gummifadens)

Nach Einführung des Kraftmaßes ist man geneigt, nach den Kräften zu fragen, die von verschiedenen Dingen z.B. von gedehnten Schraubenfedern (Gummifäden) ausgehen.

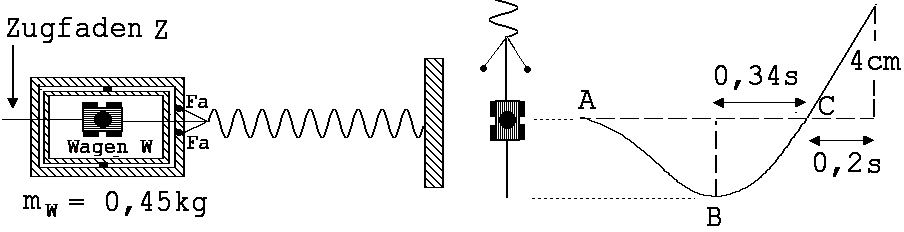
Abb. 1.3.31

In Abb. 1.3.31 ist dargestellt, wie man die Kraft einer gedehnten Schraubenfeder oder eines gedehnten Gummifadens entsprechend der Definition des Kraftmaßes ermitteln kann.

Ein auf der Wippe (Abb. 1.3.31) stehender Experimentierwagen W der Masse m ist mit einer langen von 0,2 m auf 0,7m gedehnten Schraubenfeder (Gummifaden) verbunden. Ein Faden Fa, der beiderseits am äußeren Rahmen der Wippe befestigt ist, schränkt die Bewegungsfreiheit des linken Federendes auf etwa 5 cm ein. Mit Hilfe des Zugfadens Z wird der Wagen ein wenig nach links gezogen und danach losgelassen. Unter Einwirkung der Schraubenfeder (Gummifaden) schnellt der Wagen nach rechts ( an den Reibungsausgleich denken). Der Rechner zeichnet hierbei ein s-t-Diagramm des Wagens W. Der Punkt A dieses Diagramms kennzeichnet den Anfangszustand. Bei B wird der nach links gezogene Wagen freigegeben. Bei C ist die Feder wieder in ihrer Anfangslage; die Schraubenfeder (Gummifaden) wird von dem gespannten Faden Fa gehalten und wirkt deshalb nicht mehr auf den Wagen ein. Der sich an C anschließende Teil des Diagramms beschreibt eine gleichförmige Bewegung. Aus seiner Steigung kann die Endgeschwindigkeit Δv des Wagens (Geschwindigkeitsänderung des Wagens nach seiner Freigabe) bestimmt werden. Die Wirkungszeit Δt der Schraubenfeder (Beschleunigungszeit) ist gleich dem zeitlichen Abstand der Punkte B und C. Anhand der am Diagramm ablesbaren Werte erhält man für die Kraft:

F = (0,45 kg · 0,2 m/s) /0,34s = 0,26 N.

Folgendes ist zu beachten: Die Masse der Schraubenfeder sollte im Vergleich zur Wagenmasse vernachlässigbar klein sein. Andernfalls hätte auch die Masse der Feder einen messbaren Einfluss auf die Impulsänderung des Wagens. Gummifäden eignen sich für diesen Versuch besser als Schraubenfedern. Zur genauen Bestimmung der zu einer bestimmten Federdehnung gehörenden Kraft darf das rechte Federende nicht fixiert sein, es muss an ihm derart gezogen werden, dass die Federdehnung während der Beschleunigung konstant bleibt.

1.3.7 Die Momentangeschwindigkeit

In Abb. 1.3.32 sehen wir einen Experimentierwagen auf der Experimentierwippe, der durch den Luftstrom eines Föhns angetrieben wird. Solange der Wagen unter der Einwirkung eines Luftstroms steht, hat das zugehörende s-t-Diagramm einen gekrümmten Verlauf. Der Wagen wird fortwährend schneller.

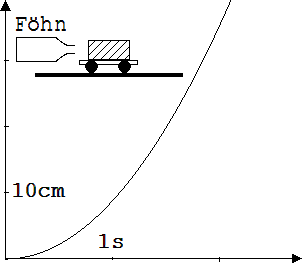
Abb. 1.3.32

Wie kann man an einem solchen Diagramm Geschwindigkeiten bestimmen ?

Im Kapitel 1.3.6.1 wurde zur Ermittlung der Geschwindigkeit der Luftstrom zum Wagen hin unterbrochen und so eine gleichförmige Bewegung mit der Geschwindigkeit v herbeigeführt. Dieses v wurde als Momentangeschwindigkeit zum Zeitpunkt t, dem Zeitpunkt der Unterbrechung angegeben. Es ist die Geschwindigkeit, die der Wagen beibehält, wenn nach t keine Kraft auf ihn einwirkt.

Nun erscheint folgendes Vorgehen angemessen:

Der Weg Δs in einem auf den Zeitpunkt t folgenden sehr kleinen Zeitabschnitt Δt wird bestimmt. Δt wird so klein gewählt, dass sich in dieser kurzen Zeit die Kraft nur wenig auf die Bewegung auswirken kann und infolgedessen Δs/Δt kaum von der Geschwindigkeit v abweicht, die sich einstellt, wenn nach t keine Kraft wirkt. Die Abweichung |Δs/Δt – v| strebt mit kleiner werdendem Δt gegen 0. Man sagt in diesem Fall, v ist der Grenzwert von Δs/Δt für Δt → 0.

An der Bilderserie in Abb. 1.3.33 ist die Entwicklung zu dem genannten Grenzwert v zu erkennen. Durch Anfang und Ende von Kurvenabschnitten, die in Zeitintervallen Δt unmittelbar nach dem Zeitpunkt t = 1 s entstehen, werden Streecken gelegt.

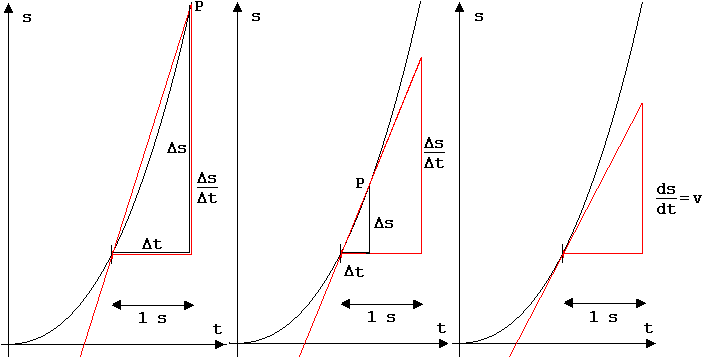
_{Abb. 1.3.33}

Die Steigung einer Strecke ist gleich dem Quotienten Δs/Δt. Mit kleiner werdendem Δt streben die Strecken gegen eine Grenzlage. Eine Gerade in dieser Grenzlage wird Tangente (Berührungsgerade) genannt, ihre Steigung ist gleich der Momentangeschwindigkeit v.

Für den Grenzwert von Δs/Δt schreibt man lim Δs/Δt ( Δt → 0) oder ds/dt ( sprich ds nach dt). Mit der Sprechweise ds nach dt anstelle von ds durch dt soll vermieden werden, dass dieser Grenzwert (Differentialquotient) als Quotient bestimmter Größen aufgefasst wird. Lim ist eine Abkürzung für Limes (Grenze).

Als Momentangeschwindigkeit v zu einem bestimmten Zeitpunkt t definieren wir nun den Grenzwert von Δs/Δt.

v = lim Δs/Δt ( Δt → 0) = ds/dt

Kann die Momentangeschwindigkeit des vom Föhn angetriebenen Wagens berechnet werden ? Dies ist erst möglich, wenn der Weg s in Abhängigkeit von der Zeit t bekannt ist. Möglicherweise besteht eine Proportionalität zwischen mittlerer Geschwindigkeit und der Zeit. Unter einer mittleren Geschwindigkeit v_m verstehen wir das Verhältnis aus einem zurückgelegten Weg s und der zugehörenden Zeit t. Diese Definition ist an keinen besonderen Bewegungsablauf geknüpft; die Bewegung kann in der Zeit t langsamer oder schneller werden.

v_m = s/t

Zur Prüfung der vermuteten Proportionalität werden am Diagramm der Abb. 1.3.32 zu verschiedenen Zeitpunkten t (t: Zeit seit Beginn der Bewegung) die zurückgelegten Wege s abgelesen und in eine Tabelle eingetragen. Wir erkennen, dass die Vermutung zutrifft. Die geringen Schwankungen in der letzten Spalte sind auf Messfehler zurückzuführen.

s/t² = 8,9 cm /s² = 0,089 m/s² = k (Konstante) → s = k · t²

Nun kann gezeigt werden, wie sich Δs/Δt mit kleiner werdendem Δt entwickelt. Die nächste Tabelle enthält Δs- und Δs/Δt-Werte zu verschieden großen Zeitabschnitten Δt, die sich an t = 1 s anschließen. Sie wurden mit s = k · t² (k = 8,9 cm/s² ) berechnet. Es ist zu erkennen, dass Δs/Δt mit kleiner werdendem Δt einem Grenzwert zustrebt.

Berechnungsbeispiel für Δt = 0,1 s :

Δs = 8,9 cm/s² ·(1,1 s)² - 8,9 cm/s²·(1 s)² = 1,869 cm

Die Momentangeschwindigkeit zum Zeitpunkt t = 1 s ist 17,8 cm/s.

Wegen 17,8 cm/s = 2 ·k · 1 s wird vermutet: v_{zum Zeitpunkt t} = 2 · k · t

Beweis:

Nach s = k · t² gilt:    Δs _{in der Zeit Δt} = k ·(t+Δt)² - k· t² → Δs/ Δt  = [ k ·(t+Δt)² - k· t² ] / Δt

Δs/ Δt = [k ·( t² + 2·t· Δt + Δt²) – k · t² ] / Δt   →   Δs/ Δt = 2 · k ·t + k · Δt

v = ds/dt = lim Δs/Δt (Δt → 0)   =   2·k·t

Wie verhält sich die Momentangeschwindigkeit zur mittleren Geschwindigkeit ?

Für die mittlere Geschwindigkeit v_m während des Zeitabschnitts Δt gilt: v_m = Δs/ Δt = k·2 ·t + k · Δt = k·t + k · (t +Δt).

k·t und k · (t +Δt) sind die halben Momentangeschwindigkeiten zu den Zeitpunkten t und t +Δt.

v_m = v_{vor Δt} / 2 + v_{nach Δt} / 2 = (v_{vor Δt} + v_{nach Δt})/2

Die mittlere Geschwindigkeit in einem Zeitabschnitt Δt ist gleich dem Mittelwert aus der Anfangs- und der Endgeschwindigkeit.

In Abb. 1.3.34 sehen wir v = 2 · k · t in Abhängigkeit von der Beschleunigungszeit t.

v/t = (2 · k · t )/ t = 2 ·k ist die Beschleunigung a.

a = 2 ·k  →   k = a/2

k = a/2 ; s = k · t²   →   s = ½ · a · t²

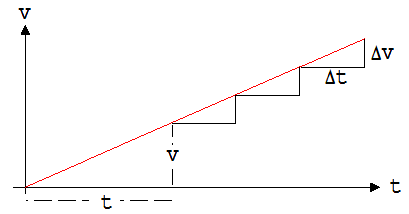
Abb. 1.3.34

Bei der Bewegung nach s = k · t² ist die Beschleunigung konstant (a = k · 2 ). Man spricht in diesem Fall von einer gleichförmig - beschleunigten Bewegung. In gleichen Zeiten erfährt das bewegte Objekt gleiche Änderungen seiner Geschwindigkeit.

Ist die Masse des beschleunigten Körpers konstant, dann zeigt eine gleichförmig-beschleunigte Bewegung eine konstante Kraft an, denn bei konstanter Masse gilt:

F = |Δ(m·v)/Δt | = m · |(Δv/Δt)| = m · |a|

Hier ist noch anzumerken, dass der oben angegebene Satz „Die mittlere Geschwindigkeit ist der Mittelwert aus der Anfangs- und Endgeschwindigkeit“ nur bei einer gleichförmig - beschleunigten Bewegung gilt.

Es stellt sich nun die Frage, welche der uns bekannten Bewegungen als gleichförmig-beschleunigt anzusehen sind. In Frage kommt z.B. die Fallbewegung eines Körpers. Wir werden diese Bewegung daraufhin untersuchen.

Aufgaben

1. Ein zunächst gleichförmig mit v₀ = 0,5 m/s über eine waagrechte Ebene rollender Wagen der Masse m = 200 g wird durch ein Gebläse Δt = 4 s lang mit F = 0,3 N in Fahrtrichtung beschleunigt. Welche Geschwindigkeit hat der Wagen nach dem Beschleunigungsvorgang ?

2. Ein Experimentierwagen mit mW = 300 g trifft auf ebener Fahrbahn mit v₀ = 3 m/s auf einen m_B = 100 g schweren Bremsklotz und schiebt diesen während des Bremsvorgangs der Dauer Δt vor sich her. Die Bremskraft, welche von der Ebene auf den Klotz ausgeübt wird, beträgt 0,5 N. Wie groß ist Δt ?

1.3.8 Der Freie Fall (Gewichtskraft)

Fallen Körper je nach Masse unterschiedlich schnell ? Ein „ja“ liegt nahe, wenn man daran denkt, dass Papierschnipsel deutlich langsamer fallen als Steine. Ein fallendes Stück Papier wird jedoch auffällig von der Luft in seinem Verhalten beeinflusst und es liegt die Vermutung nahe, dass sein langsameres Fallen auf den Luftwiderstand zurückzuführen ist, der sich bei ihm stärker auswirkt als bei einem Stein. Fallversuche in einer luftleeren Röhre bestätigen diese Vermutung und so kann man sagen: Alle Körper fallen im luftleeren Raum gleich schnell.

Ist die Fallbewegung gleichförmig beschleunigt ?

Zur Beantwortung dieser Frage dient die in der Abb. 1.3.35 skizzierte Versuchsanordnung. Ein 5 kg schwerer Metallzylinder K spult während seines Falls einen Faden von der Welle eines Dynamos (Tachogenerator ) ab. Hierbei erzeugt dieser Dynamo eine der Geschwindigkeit proportionalen elektrischen Strom. Die Masse von K ist so gewählt, dass sich die hemmende Kraft des Dynamos nicht merkbar auswirkt.

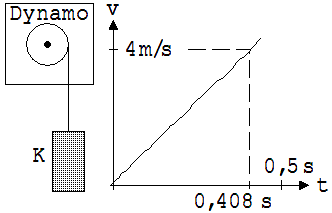
Abb. 1.3.35

Während des Falls wird die Dynamostrom in Abhängigkeit von der Zeit dargestellt. Es entsteht ein lineares Diagramm. Den Stromstärken werden die entsprechenden Geschwindigkeiten v zugeordnet, damit ein v-t-Diagramm vorliegt. Die Steigung v/t ist die Beschleunigung. 9,8m/s² kann abgelesen werden. Genauere Messungen ergeben für die ortsabhängige Fallbeschleunigung g den Wert 9,81 m/s².

Bekanntlich ist die mittlere Geschwindigkeit s/t ( s: in der Zeit t zurückgelegter Weg) gleich dem Mittelwert aus der Anfangs- und Endgeschwindigkeit. Zu Beginn der Bewegung ist die Geschwindigkeit 0, eine Zeit t später ist die Momentangeschwindigkeit gleich v.

s/t = (0+v)/2 = v/2,   v /t = g     →    v = g·t

↓

s/t = g·t / 2    →   s = (g/2) · t² Galileis Fallgesetz

Die Gewichtskraft

Die von der Erde ausgeübte Kraft (Gewichtskraft) F = m · a = m · g ist der Masse proportional, denn g ist nicht von der Masse abhängig. Auf einen Körper der Masse 1 kg wirkt die Kraft F = 1 kg · 9,81 m/s² = 9,81 N.

1.3.9 Bewegung eines Läufers (Momentanbeschleunigung)

Wie bewegt sich ein Rennläufer beim Start ? Zur Beantwortung dieser Frage dient die auf der nächsten Seite in der Abb. 1.3.36 sichtbare Messanordnung.

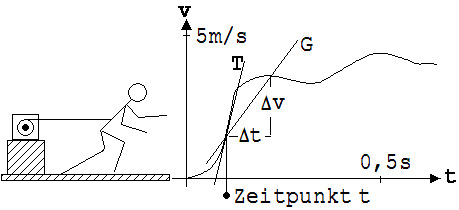
Abb. 1.3.36

Ein Läufer (65 kg schwerer Sportler) spult von der Welle eines Dynamos einen Faden ab. Da der elektrische Strom des Dynamos der Stärke nach der Geschwindigkeit des Läufers proportional ist, kann das zu diesem Vorgang gehörende Strom-Zeit-Diagramm als ein v-t-Diagramm aufgefasst werden.

Von Interesse ist die Kraft beim Anlaufen.

Zu ihrer Berechnung muss die Beschleunigung zu einem interessierenden Zeitpunkt t ermittelt werden. Am Diagramm kann die Geschwindigkeitsänderung Δv abgelesen werden, die der Läufer in einem kleinen Zeitabschnitt Δt nach einem Zeitpunkt t erfährt. Δv/Δt, der Quotient aus dieser Geschwindigkeitsänderung und der zugehörenden Zeit, ist die mittlere Beschleunigung in Δt. In Abb. 1.3.36 sehen wir eine Gerade G, deren Steigung dieser mittleren Beschleunigung gleicht. Da sich die Kraft in Δt ändert, kann aus der mittleren Beschleunigung nicht auf die Kraft F zum Zeitpunkt t geschlossen werden. Dies ist nur dann mit einem kleinen Fehler möglich, wenn Δt so klein gemacht wird, dass nur mit einer geringen Kraftänderung in diesem Zeitintervall zu rechnen ist (stetige Kraftänderung wird vorausgesetzt). Lässt man zur Verminderung des genannten Fehlers das Zeitintervall Δt nach und nach gegen 0 gehen, dann strebt die mittlere Beschleunigung gegen einen Grenzwert. Dieser Grenzwert lim Δv/Δt (Δt→ 0) wird als Momentanbeschleunigung a zum Zeitpunkt t bezeichnet. Bei Verkleinerung von Δt wird die Gerade G in eine Grenzlage gedreht. In dieser Grenzlage heißt sie Tangente T. Anhand der Tangentensteigung kann die Momentanbeschleunigung a bestimmt werden. Mit F = m · a erhält man die Kraft zum Zeitpunkt t. Für lim Δv/Δt (Δt → 0 ) = a schreiben wir dv/dt (sprich dv nach dt). Der Momentanbeschleunigung a ordnen wir den Vektor a = {dv₁/dt, dv₂/dt, dv₃/dt } zu.

Vom v-t-Diagramm zum a-t-Diagramm

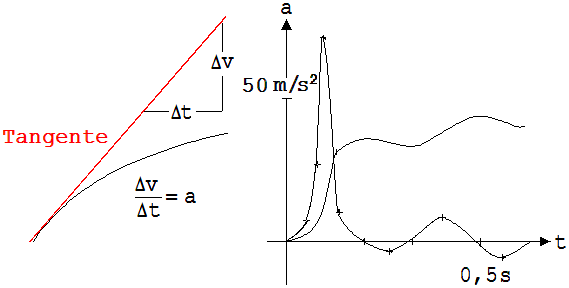
Abb. 1.3.37           Abb. 1.3.38

Beschleunigungen können am v-t-Diagramm ermittelt werden. Man erhält sie, indem man Tangenten (siehe Abb. 1.3.37) anlegt und deren Steigung bestimmt .

Das in Abb. 1.3.38 sichtbare Diagramm zeigt neben dem v-t-Diagramm eines Rennläufers das zugehörende a-t-Diagramm. Es fällt die erstaunlich hohe Anfangsbeschleunigung auf. Auf den 65 kg schweren Läufer wirken kurzzeitig etwa 4500 N.

Vom v-t-Diagramm zum s-t-Diagramm

Wenn die Geschwindigkeit konstant ist, dann kann s nach s = v · t berechnet werden. Hier ist die Geschwindigkeit leider nicht konstant. Wir müssen den Bewegungsabschnitt in viele kleine Zeitintervalle Δt zerlegen, innerhalb deren wir die Geschwindigkeiten als annähernd konstant ansehen können. Für die Wegänderung innerhalb eines solchen Intervalls können wir schreiben: Δs = Δt · v

Die Summe aller Δs gleicht dem Weg s.   →   s = Σ Δs = Σ v · Δt

Wie in Abb. 1.3.39 angedeutet ist, kann das Produkt v ·Δt durch den Flächeninhalt A einer streifenförmigen Fläche dargestellt werden. k und h beschreiben die Längen, die einer Geschwindigkeits- bzw. Zeiteinheit entsprechen.

A = (k·v)·(h·Δt) = (k·h)·(v·Δt)   →  Δs = v · Δt = A /(h·k)   →   s = Σ Δs = (Σ A) /(h·k) = A_gesamt / (h·k)

Σ A: Summe der Fächeninhalte A aller Streifen unter dem v-t-Diagramm

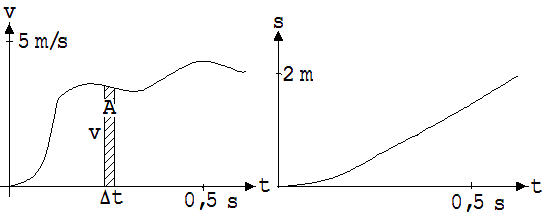
Abb. 1.3.39

Teilt man die gesamte Fläche unter dem Diagramm durch k · h, dann erhält man den insgesamt zurückgelegten Weg s. So können die Wege während verschiedener Laufzeiten für ein s-t-Diagramm bestimmt werden.

1.3.10 Über den Umgang mit Einheiten

Es gibt bekanntlich Grundeinheiten wie m, s und kg und solche Einheiten, die von diesen Grundeinheiten abgeleitet werden z.B. cm = 0,01 m, m/s, m/s², kg·m/s² usw.. Unter den Einheiten kg, m und s kann man sich noch etwas vorstellen. Anders verhält es sich mit m/s² und kg · m/s². Diese Einheiten sind formaler Natur. m/s² und kg·m/s² sollen darüber informieren, welche Größen in eine Rechnung eingehen und wie sie miteinander verknüpft werden. Angaben wie 2· kg·m/s² und 200000 ·g·cm/s² werden als gleichwertig gesehen. Zum Verständnis sollte man sich unter m, kg und s jeweils die Zahl 1 und unter cm, g, und h (Stunde) 1/100, 1/1000 und 3600 vorstellen. Hiernach ist es gleichgültig ob man den Wert einer Kraft z.B. 2·kg · m/s² in der hier angegeben Form oder aber in der Form 200000· g ·cm/s² in eine Gleichung einsetzt. Das Produkt aus Zahlenwert und der als Variable zu sehenden Einheit ist in beiden Fällen gleich groß. Entsprechendes gilt für andere Größen. Wenn in einer Gleichung gleichen Größen gleiche Einheiten zugewiesen werden, dann kann man alle diese Einheiten als Vertreter der Zahl 1 ansehen. Daraus folgt, dass in diesem Fall die Gleichung auch dann gültig ist, wenn die Einheiten weggelassen werden. Nach der Streichung der Einheiten liegt eine sogenannte Zahlenwertgleichung vor. Zahlenwertgleichungen sind unüblich, denn es soll immer deutlich bleiben, mit welchen Größen und Einheiten gearbeitet wird. Außerdem kann man oft Rechenfehler an den während der Rechnung auftretenden Einheiten erkennen. Wenn z.B. in einer Summe Summanden mit verschiedenen Einheiten auftreten, dann ist damit ein Hinweis auf einen Fehler gegeben.

Mit Hilfe von Einheiten können oft Gesetze vermutet werden.

Beispiel 1:

Wir wissen, dass auf einen gleichförmig kreisenden Körper eine zum Drehpunkt gerichtete Kraft wirkt. Wir vermuten, dass diese Kraft F von der Masse m des Körpers, seiner Geschwindigkeit v und dem Bahnradius r abhängig ist. v, r und m müssen so verknüpft werden, dass ein Term mit der Einheit kg · m/s² = N entsteht.

[m] = kg ; m mit eckigen Klammern heißt Einheit von m

[v] = m/s; [r] = m   →   [v² · m/r ] = kg · m/s²

Dies gibt Anlass zur Vermutung: F = v² · m/r

Beispiel 2:

Es wird angenommen, dass die Schallgeschwindigkeit v durch die Luftdichte ρ und den Luftdruck p bestimmt ist.

[ρ] = kg/m³;   [p] = kg/(m·s²);    [p/ρ] = m² / s²  →     Vermutung: v ~√(p/ ρ)