
1.13.1 Quer- und Längswellen, Wellengeschwindigkeit
Seilwelle

Abb. 1.13.1
In Abb. 1.13.1 ist ein Seil zu sehen, welches zwischen den Punkten A und B aufgespannt ist. Wird auf das eine Ende dieses Seils geschlagen, dann bildet sich eine Verformung aus, die sich selbständig zum anderen Ende hin mit einer Geschwindigkeit v ausbreitet. Was sich hier mit v bewegt, ist kein Teil des Seiles, sondern eine Zustandsänderung des Seils. Eine sich ausbreitende Zustandsänderung wird Welle genannt. In dem hier beschriebenen Fall spricht man von einer Seilwelle.
Die Berechnung der Geschwindigkeit, mit der sich diese Seilwelle ausbreitet erscheint zunächst sehr schwierig.
Wie soll F= m·a angewandt werden ?
Eine Änderung in der Betrachtungs-weise bringt bekanntlich oft völlig unerwartete Einsichten. Dies ist auch hier der Fall. Man muss mit den Augen eines Beobachters schauen, der die Verformung (Wellenberg) mit der Wellengeschwindigkeit v begleitet. Er sieht das Seil unter dem Einfluss von Zentralkräften FZ mit v durch einen Bogen fließen (Abb. 1.13.2).
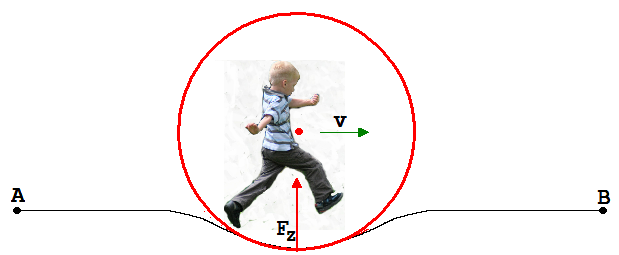
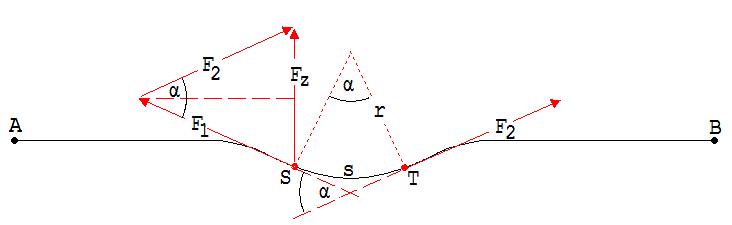
Abb. 1.13.2 Abb. 1.13.3
Wir betrachten ein Bogenstück s aus dieser Seilwelle zwischen den Punkten S und T mit der Masse m (Abb. 1.13.3). Die Zentripetalkraft Fz = m·v2 /r auf dieses Bogenstück ist die Resultierende der bei S und T angreifenden Fadenzugkräfte F1 und F2 mit übereinstimmenden Beträgen F. r ist der sogenannte Krümmungsradius von s. Hierunter verstehen wir den Radius des Kreises, der dem Bogenstück s angepasst werden kann.
Fz/2 = F· sin(α / 2) → Fz = 2·F· sin(α /2) → m·v2/r = 2·F· sin(α /2)
m/s = σ (σ = längenbezogene Dichte) → m = s·σ
s = α·r (α = Winkel im Bogenmaß) → m = α ·r ·σ
Setzt man α ·r ·σ für m in 2·F· sin(α /2) = m·v2 /r ein, dann gelangt man zu:
2·F· sin(α /2) = α·r·σ·v2/r → 2·F· sin(α /2) = α·σ·v2
Bei kleinen Winkeln α kann geschrieben werden: sin(α /2) = α /2
2·F· sin(α /2) = α·σ·v2 → 2·F· α /2 = α·σ·v2 → F = σ ·v2 → v = √(F/ σ)
Messung der Wellengeschwindgkeit
Ein dünnes Seil ist zwischen einem Scharnier Sa an der Experimentierwippe und einer um s = 5 m entfernten Rolle aufgespannt (siehe Abb. 1.12.4). Das angehängte Gewicht sorgt für eine bestimmte Zugkraft F.
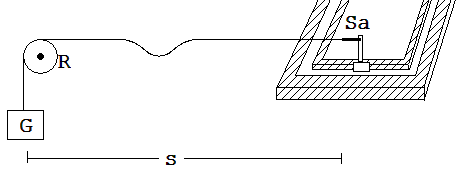
Abb. 1.13.4
Mit einem kurzen Schlag auf das Seil entsteht eine Welle, die zwischen R und Sa mehrfach hin und her reflektiert wird. Die Erschütterung, welche die Wippe bei einer Reflexion erfährt, wird von einem Rechner registriert. Die Zeitdifferenz t zwischen zwei aufeinander folgenden Erschütterungen ist die Laufzeit einer Welle entlang einer 10 m langen Strecke. 2·s/t = Wellengeschwindigkeit.
Federwelle
Eine lange Schraubenfeder der Länge L und der Masse m ist unter der Zugkraft F zwischen einer Wand und der Hand eines Schülers aufgespannt. Der Schüler zieht plötzlich ruckartig an der Feder und erzeugt damit nahe seiner Hand einen stärker gedehnten Bereich B. B bewegt sich als Welle anschließend mit einer Geschwindigkeit v über die gesamte Feder (siehe Abb. 1.13.5). Er wird an den Enden hin und her reflektiert.

Abb. 1.13.5
Wünscht man eine Gleichung für die Wellengeschwindigkeit v, dann sollte man wie im Falle der Seilwelle zum besseren Verständnis mit den Augen eines Beobachters schauen, der B mit v begleitet. Aus seiner Sicht wandert eine Windung nach der anderen von links mit der Geschwindigkeit v in B hinein. Die Windungen mit der Anfangslänge Lʼ und der Masse mʼ werden gedehnt, was zu einer Beschleunigung ihrer Schwerpunkte führt. Schließlich nimmt die Dehnung der Windungen wieder ab. Die Schwerpunkte werden auf die Geschwindigkeit v gebremst (siehe Abb. 1.13.6).
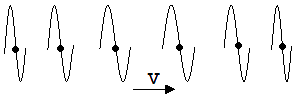
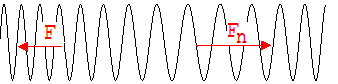
Abb. 1.13.6 Abb. 1.13.7
Wir betrachten die ersten n Windungen im Bereich B. Wir denken uns die Windungen in B von links nach rechts nummeriert. Die Nummer 1 ist gerade in B eingetreten. Auf die n Windungen wirkt insgesamt die Kraft Fn - F = mʼ·an +mʼ·an-1 + …..+mʼ·a2 + mʼ·a1 ) = mʼ·(an +an-1 + …..+a2 + a1 ). F und Fn sind die Zugkräfte an der 1. und n. Windung.
Die Zugkraft auf die n. Windung ist in B um Fn – F = mʼ·(an + an-1 + …..+ a2 + a1 ) größer geworden. Nach dem Federgesetz hat diese Windung somit in B eine Dehnung um ΔLʼ= (Fn – F)/Dʼ = mʼ·(an + an-1 + …..+ a2 + a1 )/Dʼ erfahren. Dʼ ist die Federkonstante einer Windung.
Wenn B in der Zeit Δt eine weitere Windung erfasst, dann rückt die n-1. Windung an die Stelle der n.Windung und verschiebt diese um Lʼ + ΔLʼ. Die zuvor n. Windung hat dann die Geschwindigkeit (Lʼ + ΔLʼ)/Δt = v+ΔLʼ/Δt. Somit wurde seine Geschwindigkeit in B um ΔLʼ/Δt = [mʼ·(an +an-1 + …..+a2 + a1 )/Dʼ]/ Δt vergrößert.
Diese Geschwindigkeitsänderung kann auch auf andere Art berechnet werden:
Die n. Windung hat als 1., 2. , 3. , ...n. Windung die Geschwindigkeitszuwächse a1· Δt, a2· Δt, a3· Δt, usw. erfahren.
ΔLʼ/Δt = a1· Δt + a2· Δt + a3· Δt +...........+ an· Δt = Δt·(an +an-1 + …..+a2 + a1 )
↓
mʼ·[(an +an-1 + …..+a2 + a1 )/Dʼ] /Δt = Δt·(an +an-1 + …..+a2 + a1 )
↓
mʼ/Dʼ = Δt2 → v = Lʼ/ Δt = Lʼ · √(Dʼ/mʼ)
Dʼ und mʼ können anhand der Masse m und der Federkonstanten D der gesamten Feder berechnet werden. j sei die Zahl der Federwindungen.
m = j·mʼ → mʼ = m / j
Ist eine Windung um ΔLʼ gedehnt, dann ist die gesamte Feder bei gleichmäßiger Dehnung um j · ΔLʼ verlängert. Die Kraft einer Windung gleich der Kraft der gesamten Feder.
D·j·ΔLʼ = Dʼ·ΔLʼ → Dʼ = j·D
↓
v = Lʼ·√[D·j / (m / j)] = Lʼ·√(D·j2 / m) = j·Lʼ· √(D / m); j·Lʼ ist die Federlänge L
↓
v = L· √(D / m)
Die Welle als Kraftfeld
Einen Wellenträger können wir gedanklich in viele Abschnitte gleicher Masse einteilen und jedem dieser Abschnitte eine beschleunigende Kraft F zuordnen. Nach der Richtung von F unterscheidet man Längs- und Querwellen. Ist F wie bei der Federwelle parallel zur Ausbreitungsrichtung, dann spricht man von einer Längswelle (Longitudinalwelle) , andernfalls, z.B. im Fall der Seilwelle, von einer Querwelle (Transversalwelle). Die Kräfte F bilden ein Kraftfeld.
1.13.2 Die periodische, fortschreitende Welle
Wird ein Ende eines gespannten Seils periodisch auf und ab bewegt, dann entsteht eine Welle aus periodisch wiederkehrenden gleichen Abschnitten der Länge λ (siehe Abb. 1. 13.8). λ wird Wellenlänge genannt. Der Wellenzug regt jeden Punkt P, den er erfasst, zu Schwingungen (periodisch wechselnden Zustandsänderungen) an.
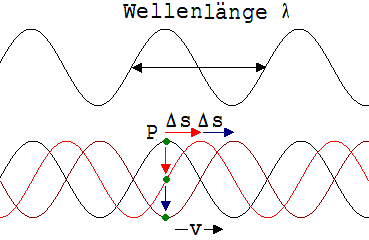
Abb. 1.13.8
P habe zu einem Zeitpunkt t seine maximale Auslenkung nach oben erreicht. Rückt die Welle danach um Δs = λ/4 nach rechts, dann nimmt P seine Mittellage ein und nach einer weiteren Wellenverschiebung um Δs = λ/4 hat P seine tiefste Lage. Ist die Welle insgesamt um λ voran gekommen, dann hat P wieder sein größte Auslenkung nach oben.
Die Schwingungsfrequenz f, die Schwingungszeit T und die Amplitude A der Punkte P sind Kenngrößen der Welle. Breitet sich eine Welle um λ aus, dann verursacht sie eine volle Schwingung von P. Daher gilt für die Wellengeschwindigkeit v:
v = λ/T ( T = Schwingungszeit); 1/T = f ( Frequenz) → v = λ · f
1.13.3 Die stehende Welle (Interferenz)
Wir stellen uns ein gespanntes Seil vor, dessen beide Enden periodisch mit gleicher Frequenz f auf und ab bewegt werden. Es bildet sich hierbei eine als stehende Welle bekannte Schwingungsform aus, die durch Stellen der Ruhe ( Knoten ) und Stellen maximaler Bewegung (Bäuche ) ausgezeichnet ist ( siehe Abb. 1.13.9 ).
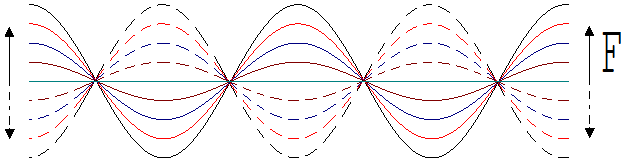
Abb. 1.13.9
Setzt man voraus, dass es sich bei gemeinsamer Wirkung mehrerer Wellen so verhält, als ob sich die den Wellen zugeordneten Kraftfelder gegenseitig durchdringen und hierbei mit der Summe ihrer Kräfte wirken, dann ist dieses Phänomen leicht erklärbar. Die Zustandsänderung an einem bestimmten Ort in einer stehenden Welle erhält man demnach, indem man die Wirkung einer nach links laufenden Welle (Kraftfeld) zu der einer von links kommenden Welle addiert.
Dieser als Interferenz (Überlagerung von Kraftfeldern) bekannte Sachverhalt wird durch Abb. 1. 13.10 veranschaulicht. Deutlich sind die Stellen (Knoten) zu erkennen, an denen sich die hin- und her laufenden Wellen in ihrer Wirkung aufheben. Der Abstand zweier benachbarter Knoten beträgt eine halbe Wellenlänge λ /2 .
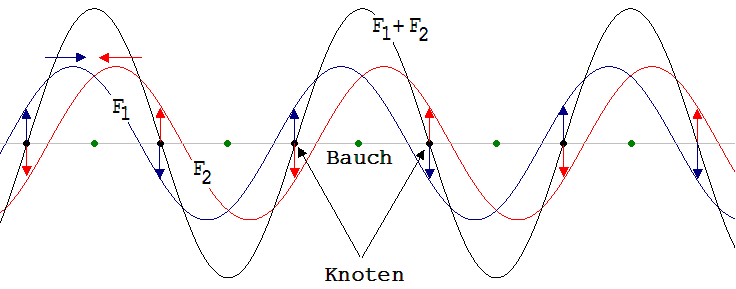
Abb. 1.13.10
Eigenschwingungen von Wellenträgern
Zwischen zwei Punkten A und B sei ein Seil der Länge L aufgespannt. Wird das Endstück bei A periodisch auf und ab bewegt, dann entsteht eine stehende Welle, die man als Ergebnis einer Interferenz zweier einander entgegenlaufender Wellen (Kraftfelder) W1 und W2 auffassen kann. W1 geht vom Wellenerreger bei A aus, W2 entsteht durch Reflexion von W1 am Ende B. Bei bestimmten Schwingungsfrequenzen wird W2 bei A so reflektiert, dass sie der bei A erzeugten Welle zugerechnet werden kann. Unter diesen Bedingungen bleibt die stehende Welle auch dann noch erhalten, wenn man das Seil nicht mehr bewegt. Man spricht in diesem Fall von einer Eigenschwingung. Die Knoten an den Enden des Seils zeigen an, dass die Kraft einer Welle bei Reflexion am festen Seilende eine Phasenumkehr erfährt. Aus + F wird -F. Nach zweimaliger Reflexion an den beiden festen Seilenden wirkt sich diese Phasenumkehr nicht aus. Deshalb ist die Bedingung für eine Eigenschwingung erfüllt, wenn der Weg einer Welle von A nach B und zurück (2 Reflexionen) ein Vielfaches der Wellenlänge λ ist.
2·L = n· λ (n: natürliche Zahl ) → λ = 2·L/n
v = λ · f
v: Wellengeschwindigkeit; f : Frequenz der Welle
f = n·v/(2·L)
Auf einem eingespannten Seil sind demnach mehrere Eigenschwingungen möglich. Die Schwingung mit n = 1 heißt Grundschwingung, die mit n = 2 erste Oberschwingung usw. .
Nach L = n· λ /2 ist bei der Grundschwingung die gesamte Seillänge gleich der halben Wellenlänge. Da zwei benachbarte Knoten eine halbe Wellenlänge voneinander entfernt sind, gibt es bei der Grundschwingung neben den Seilenden keine weiteren Knoten. Die erste Oberschwingung hat einen dritten Knoten in der Mitte.
Eigenschwingungen in einer Wasserwanne
Erzeugt man eine Welle in einer mit Wasser gefüllten Wanne, dann bildet sich eine stehende Wasserwelle aus, deren Schwingungen mit Hilfe der Experimentierwippe registriert werden können.
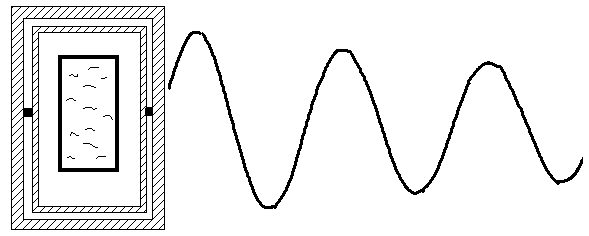
Abb. 1.13.11
Bei einer Grundschwingung ist die Länge L der Wanne gleich λ/2. Die Wellengeschwindigkeit v kann in diesem Fall nach v = λ·f = 2·L·f berechnet werden.
Eigenschwingungen einer Schraubenfeder
Die Länge L einer beidseitig eingespannten, schwingenden Schraubenfeder ist gleich n·λ/2 (n = 1 oder 2 oder 3....). Für die Geschwindigkeit v einer Längswelle auf einer Feder mit der Federkonstanten D und der Masse m wurde hergeleitet: v = L·√(D / m)
f = v/ λ; L = n·λ/2
↓
f = ( n·λ/2)· √(D / m) / λ = (n/2) ·√(D / m) → fGrundschwingung = (1/2) ·√(D / m)
Eigenschwingungen in einer Pfeife
Von einer schwingenden Stimmgabel geht eine Folge von Luftverdichtungen und Luftverdünnungen aus (siehe Abb. 1. 13.12). Der Luftdruck schwankt um den Normaldruck, wie dies durch das Diagramm in der Abb. 1. 13.12 angezeigt wird.

Abb. 1. 13.12
Zwischen zwei schwingenden Stimmgabeln gleicher Frequenz bildet sich eine stehende Schallwelle aus. Sie ist durch Bereiche mit großen Druckschwankungen Δp (Bäuche) und durch solche ohne Druckschwankungen ( Knoten) ausgezeichnet. Durch einen Knoten (ohne Druckschwankungen) strömt fortwährend Luft zu einem Wellenbauch hin oder von einem Wellenbauch fort. Eine stehende Welle in einem Rohr bewirkt mit dieser Strömung, dass im Rohr verteiltes Korkmehl an den Druckbäuchen angehäuft wird (siehe Abb. 1.13.13).

Abb. 1.13.13: Kundtscher Versuch
Eigenschwingungen in der Form stehender Schallwellen werden in einer Pfeife erzeugt. Die Abb. 1.13.14 und 1.13.15 zeigen die Beschaffenheit einer Pfeife. Wir sehen einen hohlen Rundstab mit einem schrägen Einschnitt. Ein kleiner einseitig angeschliffener Zylinder ist in die runde Öffnung eingeschoben. Er verschließt diese Öffnung bis auf einen kleinen Schlitz. Wird in diesen Schlitz geblasen, dann strömt


Abb. 1.13.14 Abb. 1.13.15
Luft gegen den Rand A des schrägen Einschnitts ( siehe Abb. 1.13.16). Es bildet sich im Hohlraum der Pfeife eine stehende Welle. Am geschlossenen Ende B ist ein Knoten bezüglich der Luftströmung und somit ein Bauch bezüglich der Druckschwankung. Bei A ist ein Bauch bezüglich der hin und her schwingenden Luft und somit ein Knoten bezüglich der Druckschwankung. Die stehende Welle in der Pfeife kann die Länge λ/4 oder 3· λ/4 oder 5· λ/4 …. haben. Die Länge L des Hohlraums ist somit ein ungerades Vielfaches von λ/4.
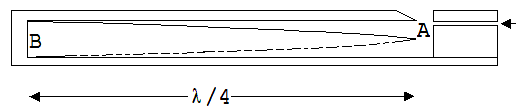
Abb. 1.13.16
Der Luftstrom gegen die Kante A wird von der Strömung in der Welle abwechselnd nach außen und innen gelenkt (siehe Abb. 1.13.17). So erhält er die Eigenschwingung.
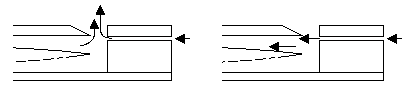
Abb. 1.13.17
Wenn nur ein einziger Druckbauch im Hohlraum der Länge L ist (Grundschwingung), dann gilt λ/4 = L. → λ = 4 · L
vSchall = λ · f ( f: Frequenz des Tons) → f = vSchall / λ = vSchall /( 4 · L)
L der oben abgebildeten Pfeife ist 9 cm.
L= 9 cm, vSchall = 330 m/s, f = 330 m/s / 0,36 m = 916 Hz
1.13.4 Interferenz von Kreiswellen
Wir stellen uns zwei Stifte vor, die regelmäßig und gleichzeitig in stehendes Wasser eintauchen. Von den Eintauchstellen gehen zwei kreisförmige, einander überlagernde Wasserwellen aus. Die kreisförmigen Wellenberge und Wellentäler, die von einem Erregungszentrum ausgehen, kann man auf dem Bildschirm eines Rechners ( z.B. mit dem Programm Mathe.-Physik) durch rote und grüne Ringe darstellen (siehe Abb. 1. 13.18 auf der nächsten Seite).
Eine Vorstellung von der Wechselwirkung (Interferenz) zweier derartiger Kreiswellen gewinnt man, wenn man eine Kopie K dieser Darstellung so anlegt, dass das Zentrum der Kopie von dem des Originals etwa 12 Bildpunkte entfernt ist. So wird ein Bild geschaffen (siehe Abb. 1. 13.19), an dem das Wesentliche der Interferenz deutlich auffällt. Dort, wo die Farben Rot und Grün zusammentreffen, bildet sich Schwarz. Dies entspricht der Interferenz eines Wellenberges mit einem Wellental (Wellenberge und Wellentäler heben sich in ihrer Wirkung auf). Das Interferenzmuster weist Streifen maximaler Erregung und solche ohne Erregung auf.
Wird zu diesem Interferenzbild noch eine weitere Kopie K so angelegt, dass die Kreismittelpunkte (Wellenzentren) im Abstand von 12 Bildpunkten entlang einer Geraden aufeinander folgen (siehe Abb. 1.13.20), dann ist zu erkennen, dass die
Bereiche maximaler Erregung mit zunehmender Zahl der Wellenzentren, die mit konstanten Abständen in gerader Linie angeordnet sind, schmaler und ausgeprägter werden (siehe Abb. 1.13.20). Abb. 1.13.21 wurde durch Überlagerung von 20 Ringsystemen mit jeweils 1 Bildpunkt Abstand erhalten. An diesem Bild erkennen wir:
Gehen von vielen direkt nebeneinander liegenden Punkten Kreiswellen aus, dann bildet sich ein Strahl.

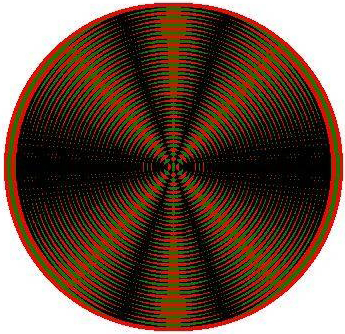
Abb. 1. 13.18 Abb. 1.13.19
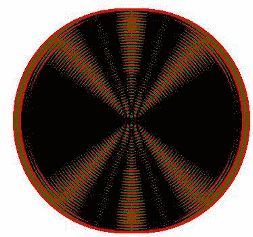
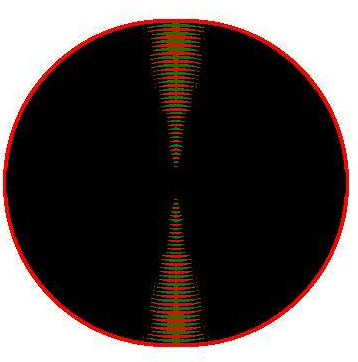
Abb. 1.13.20 Abb. 1.13.21
1.13.5 Über die Wellennatur des Lichtes
Trifft eine Welle mit gerader Wellenfront, wie in der Abb. 1. 13.22 angedeutet, auf einen Schirm mit einem Doppelspalt, dann entstehen hinter den beiden Spalten Halbkreiswellen und bilden ein Interferenzmuster. Auch das Licht zeigt solche Interferenzerscheinungen, weshalb wir von Lichtwellen sprechen können. Lässt man z.B. einen Laserstrahl auf einen Doppelspalt ( Abstand der Spalte = Gitterkonstante g ≈ 10 µ = 10-2 mm ) fallen, dann sehen wir auf einem Schirm hinter dem Doppelspalt helle und dunkle Streifen, welche Interferenzmaxima und Interferenzminima anzeigen (siehe Abb. 1. 13.22).
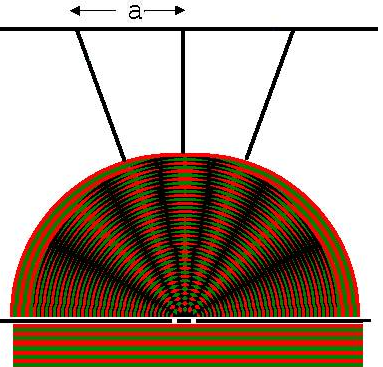
Abb. 1.13.22
Die hier beschriebene Erscheinung ermöglicht auch die Bestimmung einer Lichtwellenlänge λ (siehe Abb. 1. 13.23). Ein Punkt P des Schirms liegt dann in einem Lichtmaximum, wenn sich seine Abstände s1 und s2 von den beiden Spalten entweder nicht oder um ein ganzzahliges Vielfaches von λ unterscheiden.
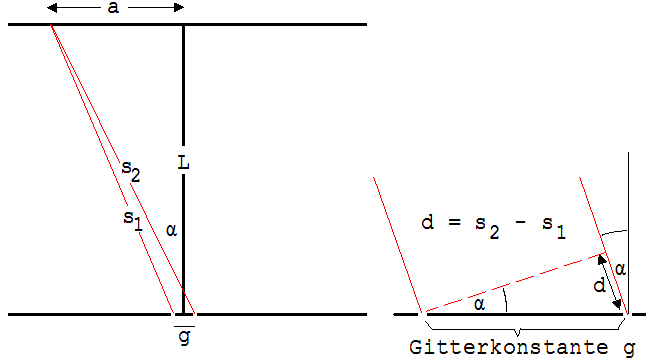
Abb. 1.13.23 Abb. 1.13.24
Unter diesen Bedingungen kommt ein Wellenberg von einem Spalt zu einem Wellenberg des anderen Spalts.
Ist s1 = s2 , dann spricht man vom Maximum 0. Ordnung.
Ist |s1 – s2| = λ , dann hat man ein Maximum 1. Ordnung usw..
a sei der auf dem Schirm erkennbare Abstand zwischen dem Maximum 0.Ordnung und einem Maximum 1.Ordnung (siehe Abb. 1.13.23).
s2 – s1 = λ
Da g im Vergleich zu L (Abstand des Schirmes vom Doppelspalt) sehr klein ist, können die Strecken s1 und s2 als parallel behandelt werden. Unter dieser Voraussetzung kann die Differenz d = s2 - s1, wie in der Abb. 1.13.24 angedeutet, berechnet werden.
d = λ = g · sin α
Mit Blick auf die Abb. 1. 13.23 (g ist sehr klein) können wir tan α = a/L setzen. Das zum Maximum 1. Ordnung gehörende α ist so klein, dass sin α ≈ tan α ist.
sin α ≈ a/L; λ = g · sin α → λ ≈ a · g/L
Wenn statt des Laserlichts weißes Licht auf den Doppelspalt fällt, dann erhält man violette, blaue, grüne, gelbe , orange und rote Linienmuster auf dem Schirm. Dies zeigt an, dass weißes Licht eine Mischung aus Wellen unterschiedlicher Wellenlängen ist. Den verschiedenen Wellenlängen sind bestimmte Farbeindrücke zuzuordnen. Die Lichtwellen, die einen Farbeindruck in unserem Auge hinterlassen, haben Wellenlängen zwischen 0,4 µ (Violett) und 0,7 µ (Rot).

Abb. 1.13.25