1.10. Über die Bewegung von Planeten

1.10.1 Berechnung einer Planetenbahn

Eine unter der Gravitationskraft der Sonne ablaufende Planetenbewegung kann wie der Wurf mit Reibung mit einem Tabellenkalkulationsprogramm quantitativ behandelt werden. Die Kraftkomponenten F_x = F₁ und F_y = F₂ in der x- und y-Richtung eines von der Sonne ausgehenden Koordinatensystems werden wie folgt berechnet (siehe Abb. 1. 10.1).

Zur Berechnung einer Planetenbahn wurden diese Kräfte in die schon mehrfach genutzte Tabelle eingetragen. Das Koordinatensystem hat seinen Nullpunkt in der Sonne. Als Anfangswerte für einen Planeten der Masse m = 2·10⁸ kg wurden folgende Werte gewählt:

1.10.2 Die Keplerschen Gesetze

An berechneten Planetenbahnen kann die Gültigkeit der drei Keplerschen Gesetze überprüft werden. Johannes Kepler entdeckte sie bei der Auswertung von Messwerte des dänischen Astronomen Tycho de Brahe, der mit ihm am kaiserlichen Hof in Prag als Mathematiker und Hofastrologe um das Jahr 1600 tätig war.

1. Keplersches Gesetz

Die Planeten bewegen sich auf Ellipsen um die Sonne, welche in einem Brennpunkt der Ellipse steht.

Definition: Zu einer Ellipse gibt es zwei Punkte B₁ und B₂, deren Abstände zu einem gegebenen Ellipsenpunkt eine von der Wahl dieses Punktes unabhängige Summe ergeben. B₁ (Sonne) und B₂ werden Brennpunkte genannt (siehe Abb. 1. 10.2).

2. Keplersches Gesetz

In gleichen Zeiten überstreicht die Verbindungsstrecke Sonne-Planet inhaltsgleiche Flächen (siehe Abb. 1.10.3).

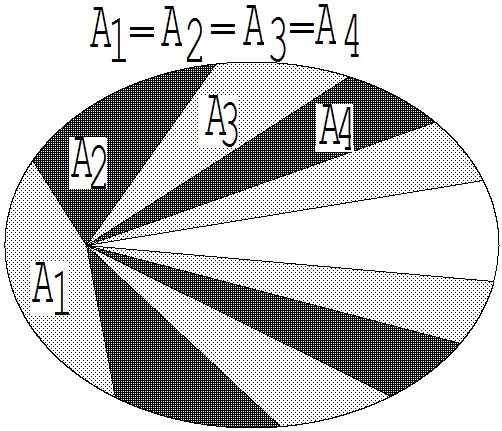
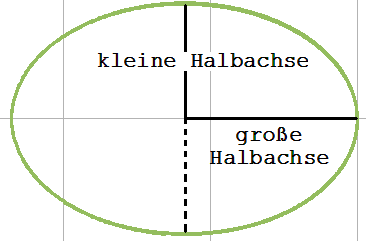
Abb. 1.10.3                              Abb. 1.10.4

3. Keplersches Gesetz

Misst man zu verschiedenen Planetenbahnen die Umlaufzeiten T und die großen Halbachsen a (siehe Abb. 1.10.4), dann gelangt man zu : a ³ / T ² = Konstante

1.10.3 Die Flächengeschwindigkeit (das Vektorkreuzprodukt )

Das 2. Keplersche Gesetz gilt für jede Bewegung unter einer Zentralkraft, einer Kraft, die auf ein bestimmtes Zentrum gerichtet ist.

Zu seiner Prüfung muss eine Gleichung zur Berechnung der Flächengeschwindigkeit v_A hergeleitet werden. Unter v_A verstehen wir das Verhältnis A/Δt. A ist die Fläche, welche in der Zeit Δt von der Verbindungsstrecke r zwischen der Sonne S und dem Planeten P überstrichen wird.

In der Abb. 1.10.5 ist die Bewegung während eines kleinen Zeitabschnitts Δt dargestellt.

Zum Beweis der Konstanz von v_A muss gezeigt werden, dass dv_A/dt = 0 ist.

dv_A/dt = 0,5 · (- dv₁/dt · y - v₁ · dy/dt + dv₂/dt· x + v₂ · dx/dt)

dx/dt = v₁ ; dy/dt = v₂ ; dv₂/dt = a₂ ; dv₁/dt = a₁

dv_A/dt = 0,5 · (-a₁ · y - v₁ ·v₂ + a₂ · x + v₂ · v₁) = 0,5 · (-a₁ · y + a₂·x )

dv_A/dt = 0,5 · {a₁ , a₂ } · {-y, x}

{a₁ , a₂ } ist parallel zu r, bildet deshalb einen rechten Winkel mit {-y, x}

↓

{a₁ , a₂ } · {-y, x} = 0

Bei einer zu r parallelen Kraft ist {a₁ , a₂ } · {-y, x} = 0. Demnach ist v_A während einer Bewegung unter einer Zentralkraft konstant. Das zweite Keplersche Gesetz ist somit bewiesen.

Hier wurde die Produktregel der Differentialrechnung angewandt. Nach ihr erhält man den Differentialquotienten eines Produktes f(t)· g(t) zweier Funktionen f(t) und g(t) mit der Summe (d f(t)/dt) · g(t) + f(t) · (d g(t)/dt ). -v₁·y ist ein solches Produkt. -v₁ und y sind als f(t) und g(t) aufzufassen.

Herleitung der Produktregel:

f(t+∆t)· g(t+∆t) - f(t)· g(t) = ∆[f(t)· g(t)]

∆[f(t)· g(t)] = f(t+∆t)· g(t+∆t) - f(t)· g(t+∆t) + f(t)· g(t+∆t) - f(t)· g(t)

∆[f(t)· g(t)] = g(t+∆t) · [f(t+∆t) – f(t)] + f(t)·[g(t+∆t)- g(t)]

∆[f(t)· g(t)]/ ∆t = g(t+∆t)· [f(t+∆t) – f(t)]/∆t + f(t)·[g(t+∆t)- g(t)]/ ∆t

d[f(t)· g(t)]/ dt = g(t)· ( df(t)/dt ) + f(t)· ( dg(t)/ dt )

Der Flächengeschwindigkeit eines Körpers K ordnen wir einen Vektor v_A mit |v_A| = v_A zu, der mit seiner Richtung die Orientierung der Ebene E anzeigt, in der sich r dreht.  v_A steht so senkrecht auf E, dass ein Betrachter mit Blick auf die Vektorspitze r in einer Linksdrehung (einer positiven Drehung) sieht.

V_A ={0; 0; 0,5· (x ·v₂ -y·v₁)} gilt für die Projektion des rotierenden Körpers auf die x-y-Ebene.

V_A={0; 0,5·(-x ·v₃ + z· v₁);0} gilt für die Projektion des rotierenden Körpers auf die x-z-Ebene.

V_A ={0,5· (y ·v₃ -z · v₂); 0;0} gilt für die Projektion des rotierenden Körpers auf die y-z-Ebene.

Behauptung: v_A = 0,5· { (y ·v₃ -z · v₂ ) ; (-x ·v₃ + z· v₁ ); (x ·v₂ -y·v₁) }

Die Richtigkeit dieser Behauptung muss gezeigt dass werden, dass 0,5· { (y ·v₃ -z · v₂ ) ; (-x ·v₃ + z· v₁ ); (x ·v₂ -y·v₁) } = {v_A1; v_A2; v_A3} ist. Wir beschränken uns auf den Beweis: 0,5· (x ·v₂ -y·v₁) = v_A3.

A (in der Abb.1.10.6 in Seitenansicht) ist die Fläche, welche der Punkt P mit seiner Verbindungslinie zum Drehpunkt in der Zeit t überstreicht. A_z ist Fläche, welche der Punkt P', die Projektion von P auf die x-y-Ebene, mit seiner Verbindungslinie zum Drehpunkt in der Zeit t überstreicht.

v_A3 = | v_A| · cos(α) = A/t · cos(α) = A · cos(α)/t

A · cos(α) = A_z → A · cos(α)/t = A_z/t = 0,5· (x ·v₂ -y·v₁)

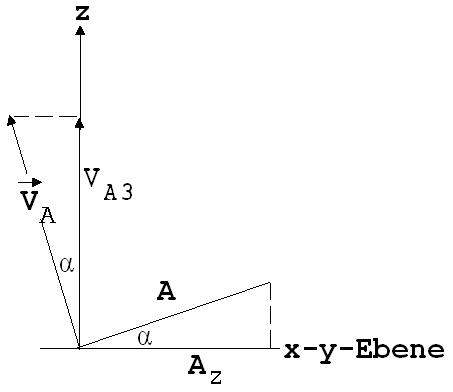
Abb. 1.10.6

{ y· v₃ – z · v₂ ; z· v₁ – x · v₃ ; x· v₂ - y · v₁ } wird Kreuzprodukt r x v aus den Vektoren r und v genannt. Diese Bezeichnung verdankt der angegebene Vektor der nun folgenden Regel zur Berechnung seiner Koordinaten. Die Koordinaten der beiden Vektoren r und v werden nebeneinander in Säulen angeordnet.

Zur Berechnung der n. Koordinate von r x v wird die n. Zeile gestrichen. Anschließend wird der erste Wert der verkürzten 1. Spalte mit dem zweiten Wert der anderen Spalte und hiernach der zweite Wert der ersten mit dem ersten Wert der zweiten Spalte multipliziert. Schließlich wird das zweite Produkt vom ersten subtrahiert. Bei Berechnung der y-Koordinate ist dann noch das Vorzeichen der Differenz umzukehren.

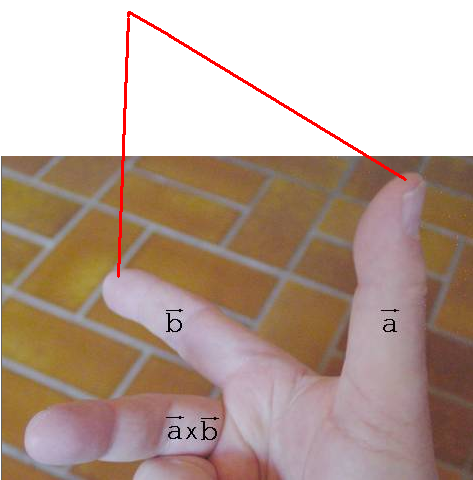
Abb. 1.10.7

Es muss angemerkt werden, dass Kreuzprodukte nicht nur aus Orts- und Geschwindigkeitsvektoren, sondern aus vielerlei Vektoren a und b gebildet wird.

a x b = { a₂·b₃ – a₃ · b₂ ; a₃· b₁ – a₁· b₃ ; a₁·b₂ – a₂ · b₁ }

a, b und a x b verhalten sich der Richtung nach wie der Daumen, der Zeige- und der Mittelfinger der rechten Hand, wenn der Mittelfinger von den beiden anderen rechtwinklig abgespreizt ist ( Rechte-Hand-Regel ). |a x b| wird durch den Flächeninhalt des von a und b aufgespannten Parallelogramms beschrieben. Als Flächeneinheit wird hierbei ein Rechteck vorausgesetzt, dessen Seiten der Länge nach mit den zu a und b gehörenden Einheitsvektoren übereinstimmen.

1.10.4 Masse der Sonne

Zur Berechnung einer Planetenbahn wurde als Masse der Sonne der Wert 2·10³⁰ kg angegeben.

Wie konnte dieser Wert bestimmt werden ?

Die Bahn der Erde um die Sonne ist fast kreisförmig (Radius r ≈ 150·10⁹ m). Deshalb ist die Anziehungskraft F der Sonne auf die Erde die Zentripetalkraft F = M_Erde · ω² · r.

F = G · (M_Sonne · M_Erde) /r²  =   M_Erde · (2 · π / T )² · r ; T steht für ein Jahr

M_Sonne = 4 · π² · r³ /( T² · G) = 1,99 · 10³⁰ kg

1.10.5 Newtons Herleitung des Gravitationsgesetzes

Abb. 1. 10.8

Als Bahn eines Planeten mit der Masse m_P und der Winkelgeschwindigkeit ω wird eine Kreisbahn vorausgesetzt. Die Kraft der Sonne auf den Planeten ist in diesem Fall die Zentripetalkraft F.

F = m_P · ω² ·r = m_P · (2 ·π / T)² · r = m_P · 4 ·π² · r / T²

Es wird eine Gleichung gesucht, die F ausschließlich in seiner Abhängigkeit von r und den Massen m_Sonne und m_Planet zeigt. Mit Hilfe des 3. Keplerschen Gesetzes kann die Umlaufzeit T durch r ersetzt werden.

r³/ T² = Konstante = K → T² = r³ /K → F = m_P · 4 ·π² · K /r²

Hieraus schließen wir: F ~ 1/r²;   F ~ m_P

Wenn die Kraft der Sonne auf den Planeten der Planetenmasse proportional ist, dann muss diese Kraft ( sie ist nach dem Wechselwirkungsgesetz dem Betrage nach gleich der Kraft des Planeten auf die Sonne) auch der Sonnenmasse m_S proportional sein ( F ~ m_S ).

F ~ m_P ;   F ~ m_S ;  F ~ 1/r²   →   F ~ m_P · m_S / r²

Newton hat diese Proportionalitätsgleichung in der hier beschriebenen Weise hergeleitet. Die Gravitationskonstante blieb ihm unbekannt.