
1.5
Über die exponentielle Abnahme physikalischer Größen
Nach den Ausführungen des letzten Kapitels sind Exponentialfunktionen mit bc·x (b>1und c<0 oder b<1 und c>0) streng monoton fallend. Es gibt viele physikalische Größen, die nach einer Exponentialfunktion abnehmen.
Als Beispiele sollen genannt werden:
1. die Zahl radioaktiver Atome innerhalb eines radioaktiven Präparates,
2. die Temperaturdifferenz zwischen einem abkühlenden Körper und seiner Umgebung,
3. die Schwingungsweite einer abklingenden Stimmgabel und
4. der Wasserstand auslaufenden Wassers in einem Gefäß mit textilem Boden.
Das 4. Beispiel soll hier ausführlich behandelt werden.
Wasser fließt aus einem zylindrischen Gefäß mit textilem Boden (siehe Abb. 1).

Abb. 1
Die Ausflussgeschwindigkeit des Wassers ist der Gewichtskraft des im Gefäß vorhandenen Wassers proportional. Somit gilt für die Wassermenge Δm, welche in einem kleinen Zeitabschnitt Δt ausfließt:
Δm ~ m · g · Δt → Δm ~ m ·Δt → Δm/(m·Δt) = Konstante = k → Δm = k · m ·Δt
m: Masse des gerade im Gefäß stehenden Wassers; g: Erdbeschleunigung
Die Massenänderung wird durch das nachfolgende Programm beschrieben.
|m|t|h|k| = |200|0|0.03|0.2|: Anfangsbedingungen
wiederhole bis n = 1
_t;m
m = m - k*m*h
t = t+h
zurück
Mit der dritten Zeile wird die Masse am Ende des Zeitabschnitts Δt = h berechnet. m(rechts) = Masse am Ende des Zeitabschnitts Δt= h; m(links)=Masse zu Beginn des Zeitabschnitts Δt = h. Mit der vierten Zeile wird die Zeit t nach Δt = h berechnet. Die zweite Zeile veranlasst, dass der Punkt P(t; m) gesetzt und mit seinem Vorgänger verbunden wird. Die Zeile oberhalb des Programms enthält die Anfangsbedingungen.
Nach der Eingabe von „34“ und „START“ kann das Programm ausgeführt werden.
Hierbei entsteht ein Diagramm, wie es in der Abb. 2 zu sehen ist.
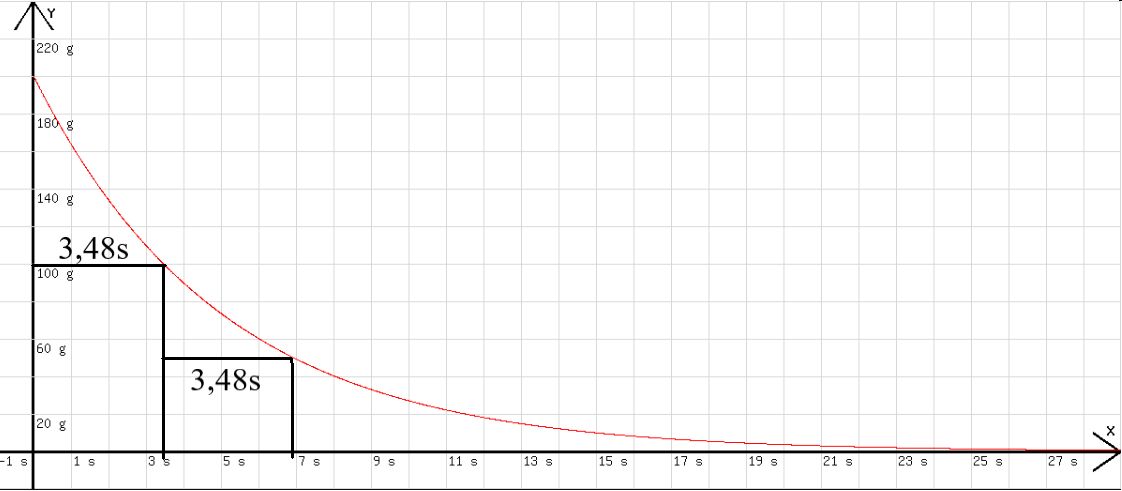
Abb. 2
An dem Diagramm fällt auf, dass innerhalb einer Zeit T = 3,48s (Halbwertszeit) eine Halbierung der vorhandenen Wassermenge stattfindet.
Dies lässt folgenden Schluss zu: m = m0 · (1/2)t/T ; m0 = 200g, T = 3,48 s
Unter dem Programm, welches mit „34“ im Tabellenfenster erscheint, steht f(t) = 200*(1/2)^(t/3.48). Wird mit einem Doppelklick auf f(t) = .... und einem nachfolgenden Rechtsklick die grafische Darstellung dieser Funktion veranlasst, dann kann keine Abweichung von dem in Abb. 2 sichtbaren Diagramm festgestellt werden. f(t) = 200*exp(-k*t) steht ebenfalls unter dem genannten Programm. Es kann somit schnell nachgewiesen werden, dass f(t) = 200*(1/2)^(t / 3.48) mit f(t) = 200*exp(-k*t) ) übereinstimmt ( exp(-k*t) = e-k·t ).