2.8 Transformationsgleichungen für eine Drehung

Abb. 1

Nach der Eingabe von „52“ und „START“ wird die Rotationsbewegung eines Elektromotors gezeigt.

Bei der Anfertigung    des   kleinen  Films  musste  der   Läufer  des  Motors   nur   in einer Stellung gezeichnet werden, denn das Bild des Läufers kann mit dem Rechner gedreht werden.

Wie führt ein Rechner die Bilddrehung aus ?

Er erfasst die Koordinaten der Bildpunkte, berechnet deren neue  Koordinaten nach einer Drehung   und ordnet diesen neuen Koordinaten Punkte zu. Zur Erfassung der Koordinaten wird  in „Mathe.-Physik“ der  Menüpunkt  „Koordinaten der  Bildschirmpunkte  in  das Tabellenfenster“ unter „Koord.“  gewählt. Um das Bild wird bei gedrückter Maustaste ein Rechteck gezogen. Ist das Rechteck vollendet, dann werden die Koordinaten in das Tabellenfenster I eingetragen. Vor  dieser Maßnahme   muss ein Koordinatensystem gesetzt  werden   (siehe „Achsensystem“  unter „Koord.“).

Zum besseren Verständnis dieses Vorgangs  soll zunächst eine  Zentrische   Streckung   durchgeführt werden. Als Urbild dient das Bild des Lehrer Lämpels aus Max und Moritz von Wilhelm Busch.

Nach der Eingabe von „11“ und „START“  erscheinen die Koordinaten des Lehrer Lämpels im  

Tabellenfenster I ( x = a; y = b) von „Mathe.-Physik“.

Mit  einem   Doppelklick   auf   2*a;2*b  werden den Punkten mit den Koordinaten a;b  (x;y) Punkte mit den Koordinaten 2·a; 2·b (2 · x; 2· y) zugeordnet.

Nach Ausführung  der  Zentrischen  Streckung wird  deutlich,  dass  zur Drehung nur eine passende Zuordnungsvorschrift fehlt.

Es stellt sich die Frage:

Wie können die Koordinaten (x; y) eines um α gedrehten Punktes P mit  Hilfe   seiner   ursprünglichen Koordinaten (x; y)  berechnet werden ?

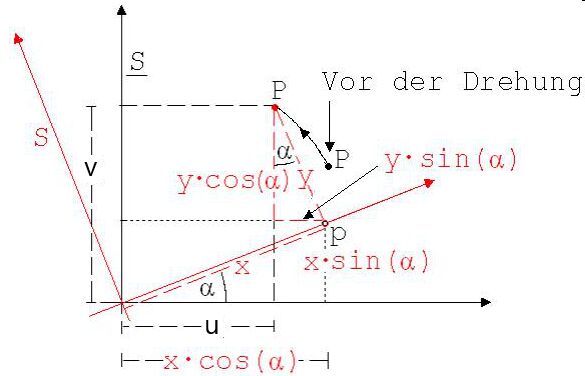
Abb. 2

Vor der Drehung gilt für P: x = x ; y = y.

Während der Drehung von P werde auch eine Kopie S des Achsensystems S um α gedreht. Infolgedessen ändern sich die x, y-Koordinaten von P  in S nicht. P wird auf einen Punkt p der x-Achse projiziert. Für die Koordinaten dieses Punktes p gilt:

  x_p = x · cosα;    y_p = x · sinα

Die x –Koordinate von P ist um y · sin α kleiner  und die y-Koordinate ist um y · cos α größer als die von p.

 x = x · cos α - y · sin α

 y = x · sin α + y · cos α

Für den Ortsvektor {x ; y } kann demnach geschrieben werden:

{x ; y } = x · { cos α ; sin α } + y ·{ -sin α ; cos α }

{ cos α ; sin α } und { -sin α ; cos α } sind Einheitsvektoren i und j , welche die Richtung der x und y Achse anzeigen.

Die Gleichung {x ; y } = x · i + y · j ist unmittelbar verständlich.

Die  hergeleiteten Transformationsformeln werden nun  zu   einer   120° -    und einer 240° - Drehung genutzt. Wieder dient der Lehrer Lämpel als Urbild. Zur 120° - Drehung wird  a*cosg(120°) - b*sing(120°); a*sing(120°) + b*cosg(120°)   über  die Tabelle  der Koordinaten geschrieben und doppelt  angeklickt . a  und  b  entsprechen x  und y, das g  hinter   sin  und  cos  zeigt  dem  Rechner  an,  dass  mit  Altgrad  gearbeitet wird.

Nach Eingabe von „53“ und „START“ kann die Drehung ausgeführt werden.