2.4 Kugelvolumen und Kugeloberfläche

Volumen

Nach Anklicken dieses Zeilenanfangs  sehen wir einen Zylinder mit einer kegelförmigen Bohrung und eine Halbkugel. Beide Körper stimmen in der  Grundfläche  und der Höhe überein  und  haben nach dem Prinzip des Cavalieri gleiche Volumina.

Prinzip des Cavalieri:

Haben  zwei  Körper in gleicher Höhe inhaltsgleiche  Querschnittsflächen,  dann  haben sie gleiche Volumina.

Abb. 1

A₁: Inhalt der Ringfläche in der Höhe h                A₂: Inhalt der Kreisfläche in der Höhe h

A₁ = π · r² - π· h² = π · ( r² – h²)                  A₂ = π · r’² = π · ( r² – h² )   →  A₁ = A₂

Nach Cavalieri habe beide Körper gleiche Volumina

Für das Volumen V des Zylinders mit kegelförmiger Bohrung gilt:

V = π · r² · r – 1/3 · π · r² · r = 2/3 · π · r³  ( Höhe des Zylinders = r)

V gleicht dem Volumen einer Halbkugel mit dem Radius r.

Für da Volumen V_K der Vollkugel gilt:    V_K = 4/3 · π· r³

Oberfläche

Wir suchen eine Gleichung, in welcher die Kugeloberfläche A enthalten ist. Zur  Entdeckung  einer solchen Gleichung ist die Frage hilfreich:

Was kann man mit A berechnen ?

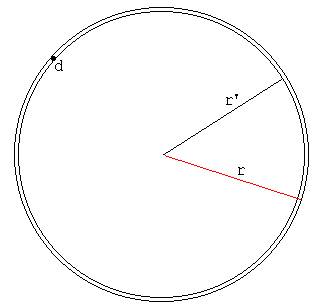
Abb. 2

Bei Kenntnis von A kann man z.B. das Volumen V einer dünnen Kugelschale der Dicke d  berechnen. Für V kann geschrieben werden:

V = A · d

A · d beschreibt das Volumen einer ungekrümmten Schicht. Die Anwendung von V = A · d  führt in dem hier vorliegenden Fall zu einem Fehler, der sich bei geringer Dicke d  jedoch kaum auswirkt. Das Volumen erhält man auch als Differenz zwischen dem Gesamtvolumen 4/3 · π · r³ und dem Hohlraumvolumen 4/3 · π · r’³.

V =  4/3 · π · r³ - 4/3 · π · r’³  →     V = 4/3 · π · ( r³ – r’³) = 4/3 · π · ( r – r’) · (r²+ r· r’ + r’²),  ( r – r’) = d

↓

V = 4/3 · π · d · (r²+ r· r’ + r’²)     →   A · d ≈ 4/3 · π · d · (r²+ r· r’ + r’²)

↓

 A ≈ 4/3 · π · (r²+ r· r’ + r’²)

Für r’ → r strebt der durch die Flächenkrümmung bedingte  Fehler gegen 0.

↓

A = 4/3 · π · (r²+ r· r + r²) = 4 · π · r²