7. Irrationale Zahlen

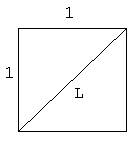
Es soll die Länge L der Diagonalen eines Quadrats mit der   Seitenlänge   1 Längeneinheit   berechnet werden (siehe Abb. 1 ).

Abb. 1

Nach dem Pythagoras gilt:  L² = 1² + 1² = 2;  √(2)

Durch Iteration findet man  √(2)= 1.4142135623731.. . Eine Periodizität oder eine Ende der Dezimalbruchentwicklung stellt sich auch nach sehr vielen Iterationsschritten nicht ein. Man gewinnt den Eindruck, dass dem Term   √(2)  weder  ein  endlicher noch ein periodischer Dezimalbruch zugeordnet werden kann. Wenn dies der Fall sein sollte, dann  gibt  es keinen Bruch a/b    (a; b: natürliche Zahlen )  mit der Eigenschaft  √(2) = a/b,  denn  jeder  Bruch a/b  kann durch   einen  endlichen  oder  periodischen Dezimalbruch dargestellt werden.

Diese Vermutung wirkt zunächst sehr verunsichernd, denn den Begriff Zahl verbinden wir in der Regel mit der Vorstellung einer ganzen Zahl oder eines Bruches.  Anders geartete   Zahlen   können wir uns zunächst nicht vorstellen.

Hier muss daran erinnert werden,  dass  wir  Zahlen durch Punkte (Einschnitte) auf einer Zahlengeraden darstellen. Ein Einschnitt E auf der Zahlengeraden können wir deshalb auch als Zahl sehen.   Wenn ein solcher Einschnitt innerhalb einer Einheitsstrecke liegt, dann repräsentiert er neben einem  ganzzahligen Anteil noch den Bruchteil einer Einheit.

Dieser Bruchteil kann nur dann durch einen  Bruch dargestellt werden, wenn eine Einheit so in n  Abschnitte gleicher Länge aufgeteilt werden kann,  dass  E genau am Ende eines solchen Abschnitts liegt. Wenn das  Ende des m. ten Abschnitts auf  E liegt, dann wird der Bruchanteil von E durch m/n beschrieben  (siehe  Abb.2).

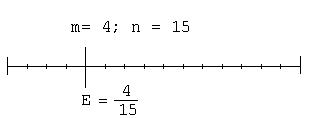
Abb. 2

Wenn man zwei Strecken durch  ganzzahlige Vielfache  einer   kleineren   Strecke darstellen  kann, dann nennt man sie  kommensurabel. Es ist denkbar, dass der Bruchanteil  von √(2)  nicht mit  einer   Längeneinheit   kommensurabel ist.

In diesem   Fall ist √(2) nicht durch eine rationale Zahl a/b darstellbar. Nach Vorgabe einer zulässigen Abweichung A kann man jedoch immer einen Dezimalbruch  angeben,  dessen   Abweichung von E geringer ist als A. Wenn z.B. die Abweichung kleiner als  1/1000000 sein soll, dann wird man die Einheit, in der E liegt,  in  1000000 Abschnitte einteilen. Der unmittelbar vor E  liegenden Teilungsmarke kann ein Dezimalbruch zugeordnet werden, der von E weniger als 1/1000000 abweicht.

Es soll nun bewiesen werden, dass √(2) nicht durch einen Bruch dargestellt werden kann.

Wir führen den Beweis indirekt.

Wir nehmen an, dass die Gegenbehauptung ( √(2)= a/b)    zutrifft  und   zeigen, dass die Folgerungen  hieraus falsch sind.

a/b (echter  oder unechter Bruch )  kann  zunächst so gekürzt werden, dass der Zähler und  der Nenner keinen gemeinsamen Teiler haben.

a/b = p/q (p und q sind teilerfremd)

√(2)  =  p/q    →     2 =  p²/q²     →      2·q² = p²         →   p² ist demnach durch 2 teilbar

Wenn p² durch 2 teilbar ist, dann  ist auch p durch 2 teilbar, denn das Quadrat   einer   ungeraden Zahl ist ungerade.

Beweis:

Jede ungerade Zahl kann man als Summe einer geraden Zahl n und der Zahl 1 darstellen.

(n+1)² = n² + 2·n + 1

Da n² +2·n gerade ist folgt: n² + 2·n + 1 ist ungerade

2·q² = p²      →        q² = p²/2 = (p/2) · p

Da p/2 eine ganze Zahl und p eine gerade Zahl ist folgt:   q² und q sind gerade Zahlen.  Somit sind p und q im Widerspruch zu der Voraussetzung nicht teilerfremd.

Hieraus schließen wir:  Es gibt keinen Bruch   a / b   =   √(2)

Wir können √(2) jedoch   entsprechend  der  Abb. 3  einen  Einschnitt E auf der Zahlengeraden zuweisen. Einschnitte,  denen  kein Bruch  zugeordnet werden kann, heißen  irrationale Zahlen.

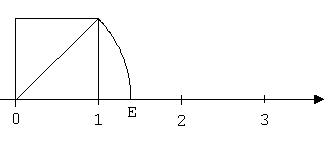
Abb. 3

Die rationalen Zahlen (echte und unechte Brüche)  fassen  wir mit den irrationalen Zahlen zur Menge der  reellen Zahlen  R zusammen.