15.
Einiges über Vektoren
a;b]: erst diese Zeile doppelt anklicken,
a+2;b+0.5]: dann diese Zeile
a+2 + 1;b+0.5+2.5: und dann diese.
| 3.8758E-1 | 6.6584E-1 |
| 3.8758E-1 | 6.5590E-1 |
| 3.8758E-1 | 6.4596E-1 |
| 3.9751E-1 | 6.9565E-1 |
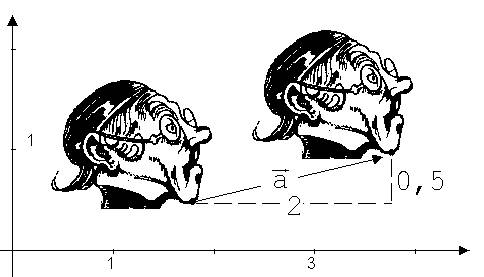
In der Tabelle stehend die Koordinaten zu den Punkten des Lehrers Lämpel. Nach einem Doppelklick auf a;b] werden die Punkte des Lehrers gesetzt und nach einem Doppelklick auf a+2;b+0.5] wird ein Bild erzeugt, welches man auch dann erhält, wenn man eine Kopie des ersten Bildes in Richtung des Pfeils a verschiebt (siehe Abb. 1).

Abb. 1
Der Verschiebungspfeil a wird Vektor genannt. Fett gedruckte Buchstaben oder Buchstaben mit einem Pfeil dienen zur Bezeichnung von Vektoren. Die Differenzen zwischen den Koordinaten seines Endpunktes (x2; y2) und denen seines Anfangspunktes (x1; y1) werden Vektorkoordinaten genannt. Die Vektorkoordinaten von a sind a1 = x2 – x1 = 2 und a2 = y2 – y1 = a2 = 0,5. Diese Vektorkoordinaten werden zu einer Zahlensäule angeordnet.
Folgende Schreibweise ist üblich:
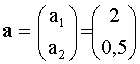
oder a = {a1 ; a2 } = {2 ; 0,5}
An der Schreibweise ist erkennbar, dass die Vektoren als einander gleich angesehen werden, die sich nur durch den Anfangspunkt unterscheiden.
Unter dem Betrag |a| eines Verschiebungsvektors a versteht man seine Länge:
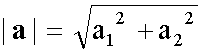
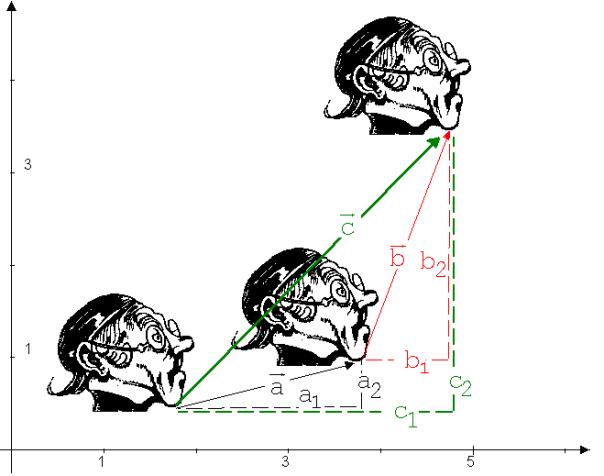
Abb. 2
Nach einem Doppelklick auf dem Befehl a +2 + 1; b+0.5+2.5 (siehe Tabelle) entsteht ein Bild, welches wie eine um c verschobene Kopie des ersten Bildes oder eine um b verschobene Kopie des zweiten Bildes aussieht.
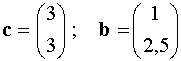
Da die Vektorkoordinaten von c durch Addition der entsprechenden Vektorkoordinaten von a und b erhalten werden, heißt c Vektorsumme von a und b. Wie in Abb. 2 angezeigt, erhält man den Summenvektor, indem man b mit seinem Fuß an die Spitze von a fügt. Der Vektor vom Fuß des Vektors a zur Spitze des Vektors b ist a+b = c. Wenn von einer Vektorsumme die Rede ist, dann wird man auch Vektordifferenzen und Produkte mit Vektoren erwarten.
Definition der Vektordifferenz:
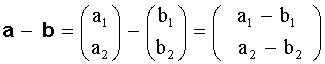
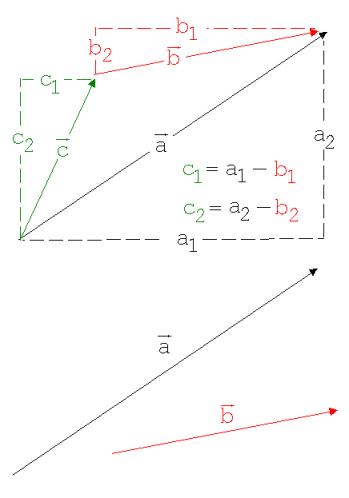
Abb. 3
Zur Bildung von a – b = c wird der Vektor b solange parallel zu sich selbst verschoben, bis er mit seiner Spitze an die Spitze von a stößt. Der Vektor vom Fuß des Vektors a zum Fuß des Vektors b ist der Differenzvektor c.
Produkt eines Vektors a = { a1 ; a2 } mit einer Zahl m ( S-Produkt).
Den Vektor { m · a1 ; m · a2 } heißt Vektor m · a . Ist m >0 , dann hat m·a die Richtung von a, andernfalls ist m ·a dem Vektor a entgegen gerichtet.
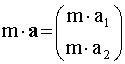
Für den Betrag von m ·a gilt: |m ·a| = |m| · |a|
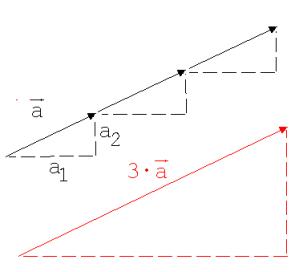
Abb. 4: Multiplikation mit m = 3
Formulierung von Abbildungsvorschriften mit Hilfe von Vektoren
Vektoren erleichtern die Formulierung von Abbildungsvorschriften.
1. Beispiel:
Aufgabe:
Der Punkt P (siehe Abb. 5) soll mit m ( beispielsweise m = -2) am Zentrum Z(u; v) zentrisch gestreckt werden. P’ sei der Bildpunkt.
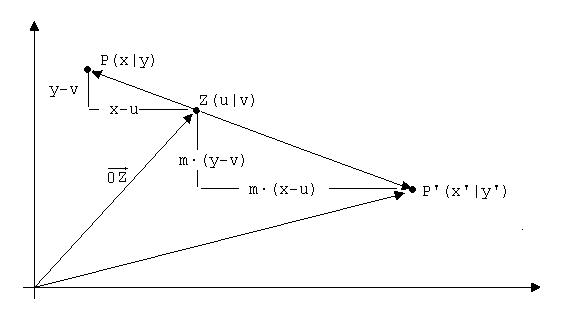
Abb. 5
Der Vektor ZP’ ist der um |m| gestreckte Gegenvektor zu ZP.
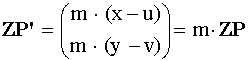
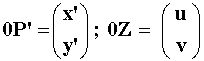
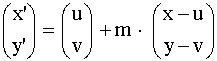
x’ = u + m · (x – u); y’ = v + m · ( y – v)
Nach Eingabe von „27“ und „START“ kann die hier beschriebene Abbildung an den Punkten des Lehrers Lämpel ausgeführt werden.
Die Abbildung mit u = 2, v =1,5 und m = - 2 ist in Abb. 6 dargestellt.
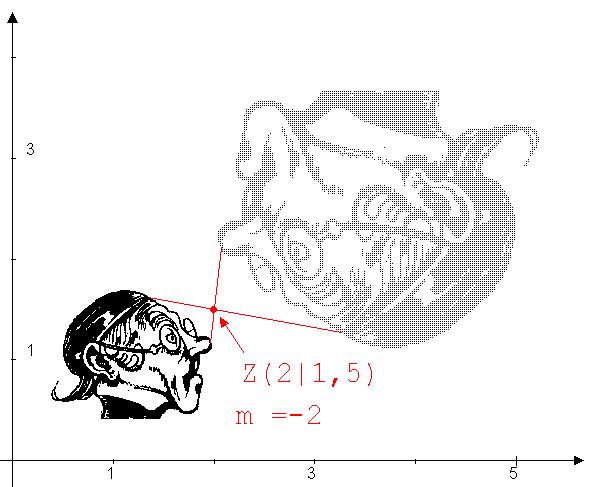
Abb. 6
Eine Abbildung mit u = 2, v =1,5 und m = - 1 ist eine Punktspiegelung an Z (siehe Abb. 7).
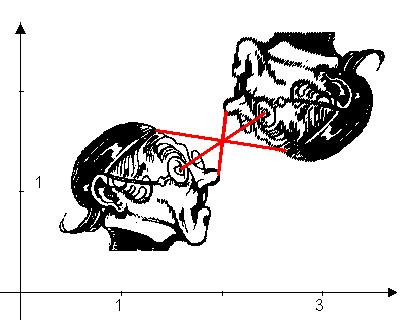
Abb. 7
2. Beispiel
In Abb. 8 ist eine Abbildung nach 0P’ = f · 0P, f = 1/(x2 + y2) dargestellt. P’ liegt auf der Halbgeraden [0P . Sein Abstand vom Nullpunkt ist gleich dem Kehrwert aus dem Abstand des Punktes P zum Nullpunkt. Diese Abbildung nennt man Spiegelung am Einheitskreis. Alle Punkte auf dem Einheitskreis (Kreis mit dem Radius eine Längeneinheit) werden auf sich selbst abgebildet, es sind Fixpunkte.
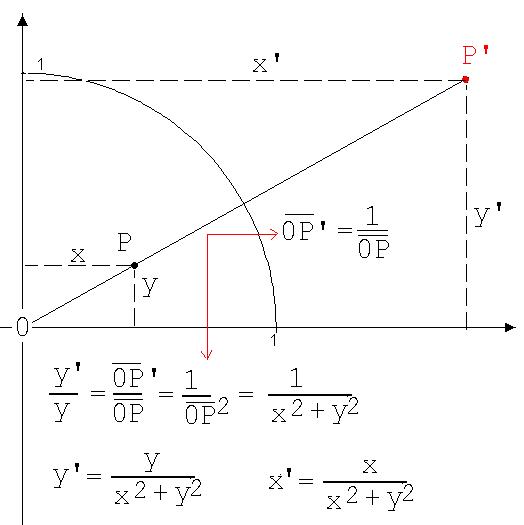
Abb. 8
Nach dem Eintrag von „28“ und „START“ kann der Lehrer Lämpel am Einheitskreis gespiegelt werden (siehe Abb. 9).
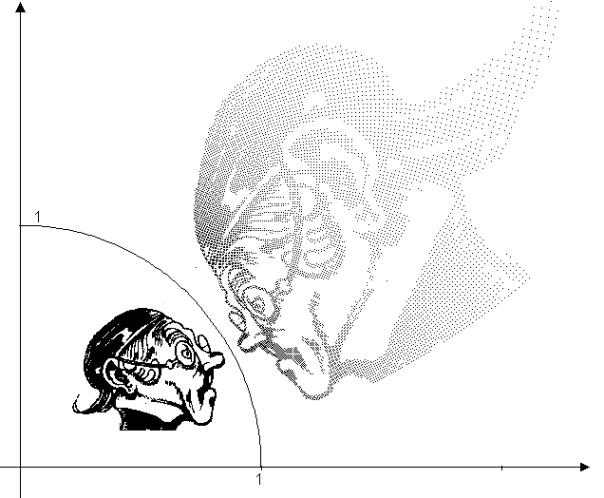
Abb. 9