12. Funktion und Umkehrfunktion

Die nachfolgende Tabelle beschreibt eine Quadratfunktion f(x) = x². Die erste Spalte enthält die Elemente der Definitionsmenge, in der zweiten Spalte sind die Elemente der Wertemenge.

x     y

| 1 |   1 |

| 2 |   4 |

| 3 |   9 |

| 4 | 16 |

| 5 | 25 |

Die nächste Tabelle unterscheidet sich von der 1. Tabelle durch die Reihenfolge der Zahlensäulen. Sie beschreibt eine Funktion y = f^*(x), die als Umkehrfunktion der Quadratfunktion bezeichnet wird.

x    y

|   1 | 1 |

|   4 | 2 |

|   9 | 3 |

| 16 | 4 |

| 25 | 5 |

y = x²   ist die Zuordnungsvorschrift zur 1.   und y =   die zur  2. Tabelle.   Die Wurzelfunktion  y =  ist somit die Umkehrfunktion der Quadratfunktion y = x².  In Abb. 1 sind beide Funktionen graphisch dargestellt.

Den Graphen einer Umkehrfunktion  erhält man  durch   Achsenspiegelung   des zur ursprünglichen Funktion gehörenden Graphen an der Geraden y = x.

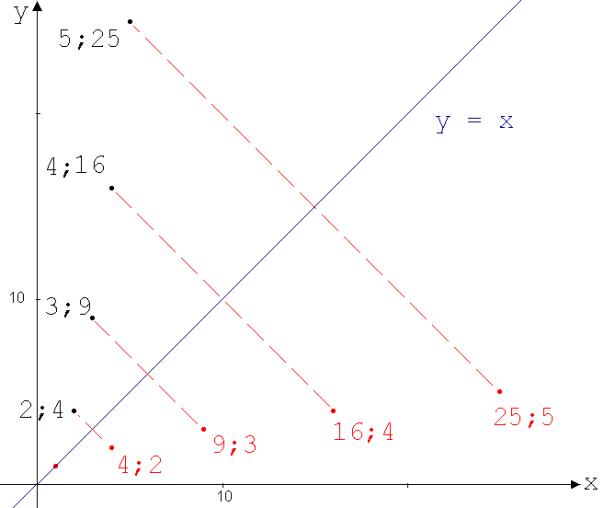
Abb. 1

Nach Eingabe von „21“ und „START“ kann die graphische Darstellung ausgeführt werden.

Vertauschung von x und y in der  Zuordnungsvorschrift einer Funktion führt zur Zuordnungsvorschrift der Umkehrfunktion.

Beispiel:

Funktion:    y = x²;  Definitionsmenge D = Menge der reellen Zahlen

Umkehrfunktion:    x = y²   →    √(x) = |y|     →      y = ± √(x) 

Es ist bekannt, dass von  einer  Funktion nur dann gesprochen werden kann, wenn y eindeutig durch x bestimmt ist.

Deshalb  kommen nur   y = + √(x)   und   y = - √(x)  als Funktionen in Frage.

y = +√(x) ist die Umkehrfunktion von y = x²  ( x ≥ 0).

y = - √(x)  ist die Umkehrfunktion von y = x²  ( x ≤ 0).

 In   Abb. 2 sind die Quadratfunktionen   y = x² ( x ≥ 0);    y = x² (x ≤ 0)   sowie  deren Umkehrfunktionen graphisch dargestellt.

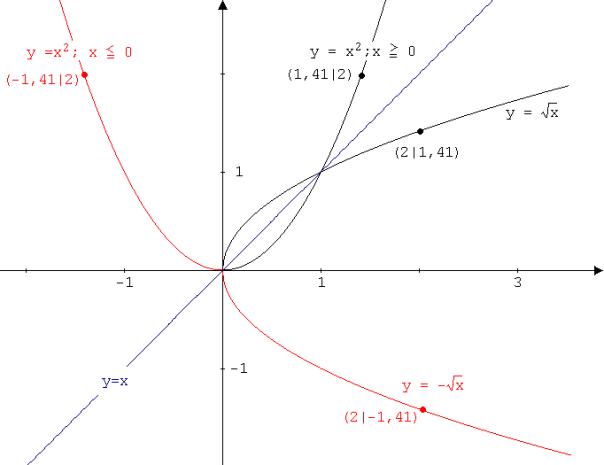
Abb. 2

Folgendes ist zu sehen:

Durch Umkehrung einer Funktion y = f(x) erhält man nur dann wieder eine Funktion, wenn y = f(x) einen streng monoton steigenden bzw. streng  monoton fallenden  Verlauf  hat,  nur dann ist sie umkehrbar.

Trifft dies nicht zu, dann hat y = f(x) zu verschiedenen x - Werten gleiche y-Werte. Nach seiner Umkehrung finden wir verschiedene Wertepaare (x; y), die im x-Wert  übereinstimmen.

Streng mononoton steigend heißt:  Einem größeren x-Wert wird immer ein größerer y-Wert zugeordnet.

Streng monoton fallend heißt: Einem größeren x-Wert wird immer ein kleinerer y - Wert zugeordnet.