1.
Der Satz des Pythagoras

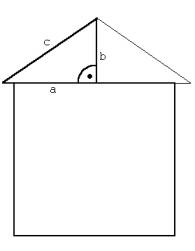
Abb. 1
Aufgabe:
Es soll ein Dach mit einer bestimmten Breite und einer bestimmten Höhe errichtet werden. Der Zimmermann muss bei Kenntnis von Breite und Höhe die Länge der Dachsparren berechnen.
Der Mathematiker beschreibt diese Aufgabe mit den Worten:
Berechne die Länge der Hypotenuse c eines rechtwinkligen Dreiecks mit Hilfe der Kathetenlängen a und b. a ist hier die halbe Dachbreite.
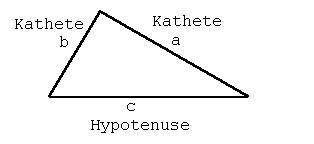
Abb. 2
Zur Lösung der Aufgabe muss eine Gleichung gefunden werden, die a, b und c enthält. Da an dem vorliegenden Dreieck keine Beziehungen zwischen den genannten Größen erkennbar sind, werden wir versuchen, Dreiecke der beschriebenen Art zu einem geometrischen Gebilde zusammenzustellen, an dem wir möglicherweise mehr Erfolg haben. So kann man vier Dreiecke zu einem Quadrat zusammenrücken, wie dies nach Anklicken dieses Zeilenabschnitts vorgeführt wird. Das letzte Bild der Serie ermöglicht die Aufstellung einer Gleichung mit a, b und c.
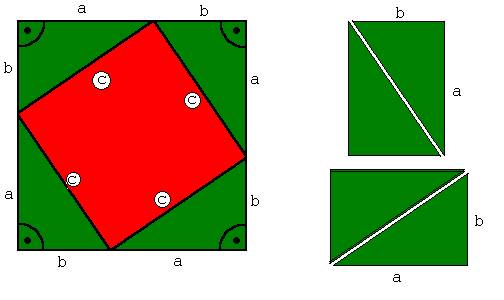
Abb. 3
Jeweils zwei Dreiecke kann man zu einem Rechteck mit der Breite b und der Länge a zusammenfassen.
↓
c2 + 2 · a · b = (a + b )2 → c2 + 2· a · b = a2 + 2 · a · b + b2
↓
c2 = a2 + b2
Satz des Pythagoras
Beispiel 1: a = 3, b = 4 → c2 = 32 + 42 = 25
c
ist eine Zahl, deren Quadrat gleich 25 ist. Wir nennen eine Zahl,
deren Quadrat gleich 25 ist, eine Wurzel aus 25 und schreiben für
sie
![]() .
.
√(25) = 5 → c = 5
Unter √(a) , a >=0, verstehen wir eine Zahl >= 0, deren Quadrat a ist.
Beispiel
2: a = 4, b = 5 → c2
= 16 + 25 = 41 → c =
![]()
Zu
den Zahlen 4, 9, 16, 25, 36,49 kann man leicht die zugehörenden
Wurzeln erraten; es sind die Zahlen 2, 3, 4, 5, 6 und 7.
Zu der Zahl 41 ist dies leider nicht so leicht möglich. Ähnlich
verhält es sich mit
![]() ,
,
![]() und
und
![]() .
.
Zur Berechnung derartiger Wurzeln wurde ein unter dem Namen „Iteration“ bekanntes Verfahren entwickelt ( siehe nächstes Kapitel).