Transformationsgleichungen für eine Drehung

von Gerhard Höhne

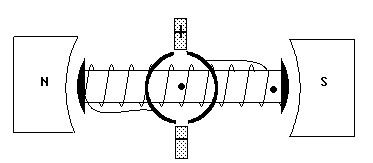
Vorbemerkung: Die Behandlung der Transformationsgleichungen zu einer Drehung wurde von den Schülern einer 10. Klasse nach einer Physikstunde gewünscht, in der ich die Funktionsweise eines Elektromotors auf einem Computerbildschirm (Projektionsdisplay) anhand der in Abb. 1 angedeuten Folge aus acht Bildern (Film) erklärt hatte. Als mich die Schüler nach der für diesen Film notwendigen Arbeitszeit fragten, sagte ich unter anderem, daß man den Läufer des Motors nur in einer Stellung zeichnen müsse, weil man sein Bild mit einem Rechner drehen könne. Ich versprach, die Bilddrehung in einer der nächsten Mathematikstunden mit Hilfe eines von mir geschriebenen Programms mit dem Namen "Mathe. - Physik" zu erläutern.

Obwohl die Tranformationsgleichungen für eine Drehung nach dem in Bayern geltenden Lehrplan nicht vorgesehen sind, ist dieses Thema mit dem Lehrplan verträglich, denn anhand der Drehung können leicht die Additionstheoreme eingeführt werden.

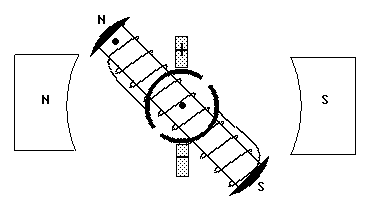
Abb. 1

Stundenverlauf

Am Anfang steht die Frage:

Wie führt ein Computer eine Bilddrehung aus?

Mit Hilfe der Schüler wird folgende Antwort formuliert:

Er erfaßt die Koordinaten der Bildpunkte, ordnet ihnen die Koordinaten gedrehter Punkte zu und stellt diese graphisch dar.

Der Lehrer stellt " Mathe. Physik " als passendes Programm vor.

Ein Computer kann mit diesem Programm die Koordinaten zu den Punkten eines Bildes lesen, in eine Tabelle eintragen und diesen Koordinaten nach beliebig wählbaren Rechenvorschriften andere Wertepaare zuordnen. Die neuen Wertepaare können graphisch dargestellt werden.

Die Möglichkeiten, die es bietet, werden an Beispielen erläutert.

So wird gezeigt, wie die den Schülern bekannten Abbildungen Achsenspiegelung und Zentrische Streckung realisiert werden können. Als Urbild dient das Bild des Lehrer Lämpels aus Max und Moritz von Wilhelm Busch.

Die Koordinaten des Urbildes werden wie folgt erfaßt:

Nachdem ein Koordinatensystem gesetzt ist, wird nach Anklicken von "Koordinaten in eine Tabelle" ein Rechteck um das Bild des Lehrer Lämpels gezogen. Anschließend liest der Rechner die Koordinaten der Bildpunkte und trägt diese in eine Tabelle ein (siehe Abb.2).

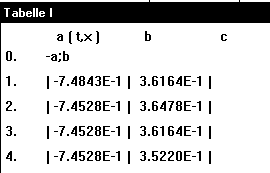
Abb. 2

Der 1. Tabellenspalte ist die Variable a der nächsten die Variable b usw. zugeordnet. Über die Tabelle wird -a;b geschrieben und hiernach "Tabelle auswerten" angeklickt. Hiernach zeichnet der Rechner Punkte mit den Koordinaten -a;b. Es entsteht ein Spiegelbild (siehe Abb.3).

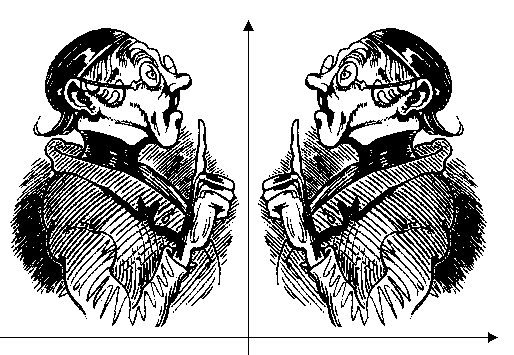
Abb. 3

Nun wird mit der Abbildungsvorschrift a*2;b*2 eine Zentrische Streckung ausgeführt (siehe Abb. 4).

Abb. 4

Nach der Achsenspiegelung und der Zentrischen Streckung wird deutlich, daß zur Drehung nur eine passende Zuordnungsvorschrift fehlt.

Es stellt sich die Frage:

Wie können die Koordinaten (x'; y') eines um a gedrehten Punktes mit Hilfe seiner ursprünglichen Koordinaten (x; y) berechnet werden ?

Die Koordinaten werden in einer Skizze ( Abb. 5) dargestellt. P' und P sind die Orte nach und vor der Drehung.

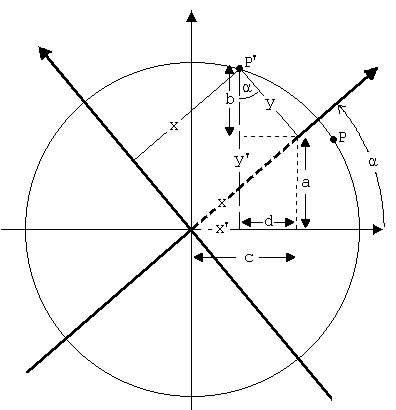
Abb. 5

Im Hinblick auf die letzte Abbildung werden die gewünschten Gleichungen schnell gefunden.

x' = c - d = x*cos(α) - y * sin(α)

y' = a + b = x*sin(α) + y*cos(α)

Die Transformationsformeln werden nun zu einer 120° - und einer 240° - Drehung genutzt (siehe Abb.6). Wieder dient der Lehrer Lämpel als Urbild.

Zur 120° - Drehung wird a*cosg(120°) - b*sing(120°); a*sing(120°) + b*cosg(120°) über die Tabelle der Koordinaten geschrieben und daraufhin "Tabelle auswerten" angeklickt . a und b entsprechen x und y, das g hinter sin und cos zeigt dem Computer an, daß mit Altgrad zu rechnen ist.

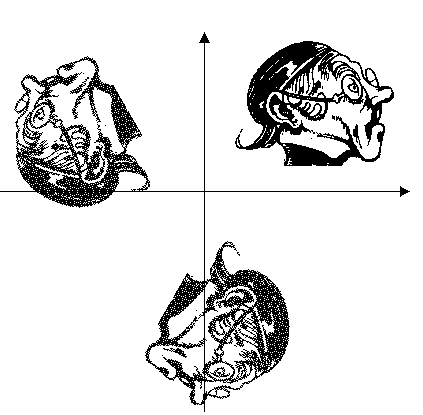
Abb. 6

Hausaufgabe:

1. Beweise, daß die zur Drehung gefundenen Gleichungen auch für Drehwinkel α

(90° < α < 180° ) gelten.

2. Ein Punkt P werde nach einer Drehung um α noch einmal um einen Winkel β

gedreht. Nach der 1. Drehung hat er die Koordinaten (x'; y') nach der 2. Drehung die

Koordinaten (x'', y'').

Es gilt:

x' = x * cos(α) - y * sin(α)

y' = x * sin(α) + y * cos(α)

x'' = x' * cos(β) - y' * sin(β)

y'' = x' * sin(β) + y' * cos(β)

x'' = x * cos(α+β) - y * sin(α+β)

y'' = x * sin(α+β) + y * cos(α+β)

Drücke sin(α+β) und cos(α+β) durch und sin(α), cos(α), sin(β) und cos(β) aus !

Bedenke, daß die oben stehenden Terme für x' und y' in die Gleichungen

des zweiten Paares eingesetzt werden können.

Veröffentlichung: BUS 37 - Themen-BUS 1999